The graph between wave number (→v) and angular frequency (ω) is
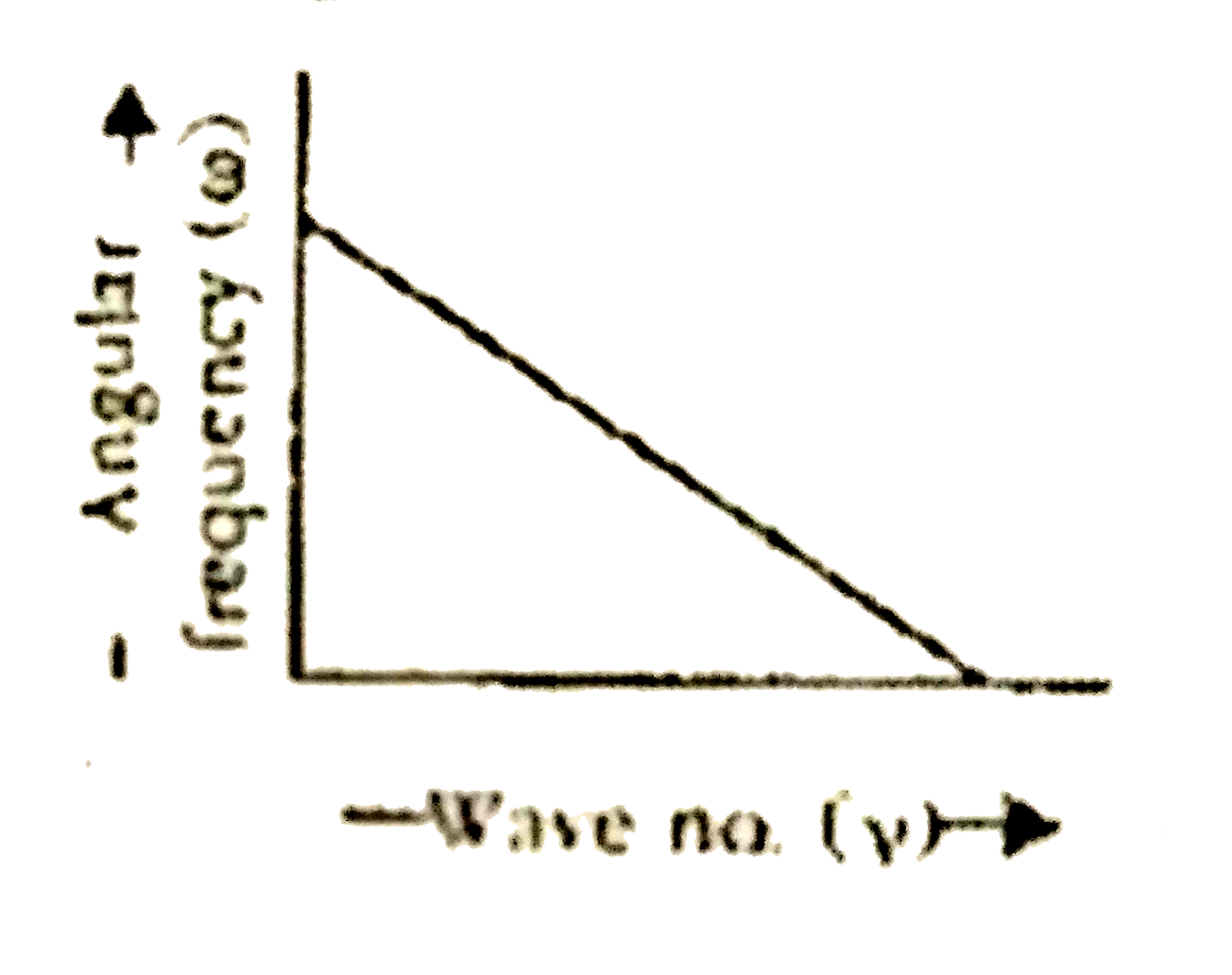
The correct Answer is:A
To solve the problem of finding the graph between wave number (ν) and angular frequency (ω), we can follow these steps:
Step 1: Understand the relationship between wave number, angular frequency, and speed of light
The speed of light (C) is related to the angular frequency (ω) and the wavelength (λ) by the equation:
C=ω⋅λ
Step 2: Relate wavelength to wave number
The wave number (ν) is defined as the reciprocal of the wavelength:
ν=1λ
Thus, we can express the wavelength in terms of wave number:
λ=1ν
Step 3: Substitute the expression for wavelength into the speed of light equation
Substituting λ in the speed of light equation gives:
C=ω⋅1ν
Rearranging this equation leads to:
ω=C⋅ν
Step 4: Identify the relationship between ω and ν
From the equation ω=C⋅ν, we see that angular frequency (ω) is directly proportional to wave number (ν). This indicates a linear relationship.
Step 5: Determine the graph
In a graph where the x-axis represents wave number (ν) and the y-axis represents angular frequency (ω), the equation ω=C⋅ν suggests that the graph will be a straight line passing through the origin. The slope of this line will be equal to the speed of light (C).
Conclusion
The graph between wave number (ν) and angular frequency (ω) is a straight line with a slope equal to the speed of light (C).
---
The speed of light (C) is related to the angular frequency (ω) and the wavelength (λ) by the equation:
C=ω⋅λ
The wave number (ν) is defined as the reciprocal of the wavelength:
ν=1λ
Thus, we can express the wavelength in terms of wave number:
λ=1ν
Substituting λ in the speed of light equation gives:
C=ω⋅1ν
Rearranging this equation leads to:
ω=C⋅ν
From the equation ω=C⋅ν, we see that angular frequency (ω) is directly proportional to wave number (ν). This indicates a linear relationship.
In a graph where the x-axis represents wave number (ν) and the y-axis represents angular frequency (ω), the equation ω=C⋅ν suggests that the graph will be a straight line passing through the origin. The slope of this line will be equal to the speed of light (C).
The graph between wave number (ν) and angular frequency (ω) is a straight line with a slope equal to the speed of light (C).
Topper's Solved these Questions
Similar Questions
A sinusoidal wave travelling in the positive x-direction has an amplitude of 15.0cm, a wavelength of 40.0cm and a frequency of 8.00Hz.Thevertic≤displacementofthemediumatt = 0 and x = 0isalso15.0 cmasshown∈figure.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V03_C17_E01_054_Q01.pngwh=80%mx-autosty≤=background:white;><br>(a)F∈dtheanga––rwaveνmberk,periodT,anga––requencyomegaandspeedv of the wave.
(b) Write a general expression for wave function.
View SolutionA series combination of an inductor (L), capacitor (C) and a resistor (R) is connected across an ac source of emf of peak value E0 and angular frequency (ω). Plot a graph to show variation of impedance of the circuit with angular frequency (ω).
View Solution
Knowledge Check
The graph between the angular momentum J and angular velocity ω will be :-
A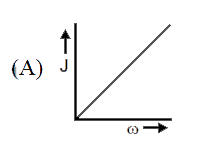 B
B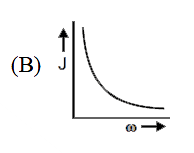 C
C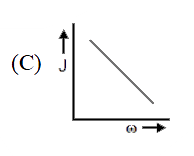 D
D
Which one of the following is the correct relation between frequency/ and angular frequency ω?
Af=πωBω=2πfCf=2ω/πDf=2πωRelation between Linear velocity (v) and Angular velocity (ω)
Av=rωBω=vωCr=vωDv=ωr
The graph between inductive reactance and frequency is
View SolutionA transverse pulse is given as y=1010x−πt where x and y are in cm and in second
Assertion: The frequency of the pulse is 120Hz
Reason: We can write this equation as y=Akx−ωt
where A .K. and ω are the amplitude,wave number and angular frequency of pulse
View SolutionWhat is the time period of a wave having angular frequency (ω) equal to 0.5s−1?
View SolutionThe relation between wavelength (λ) and angular wave number (k) of a wave is
View SolutionIn R−L−C series circuit, we have same current at angular frequencies ω1 and ω2. The resonant frequency of circuit is
View Solution

