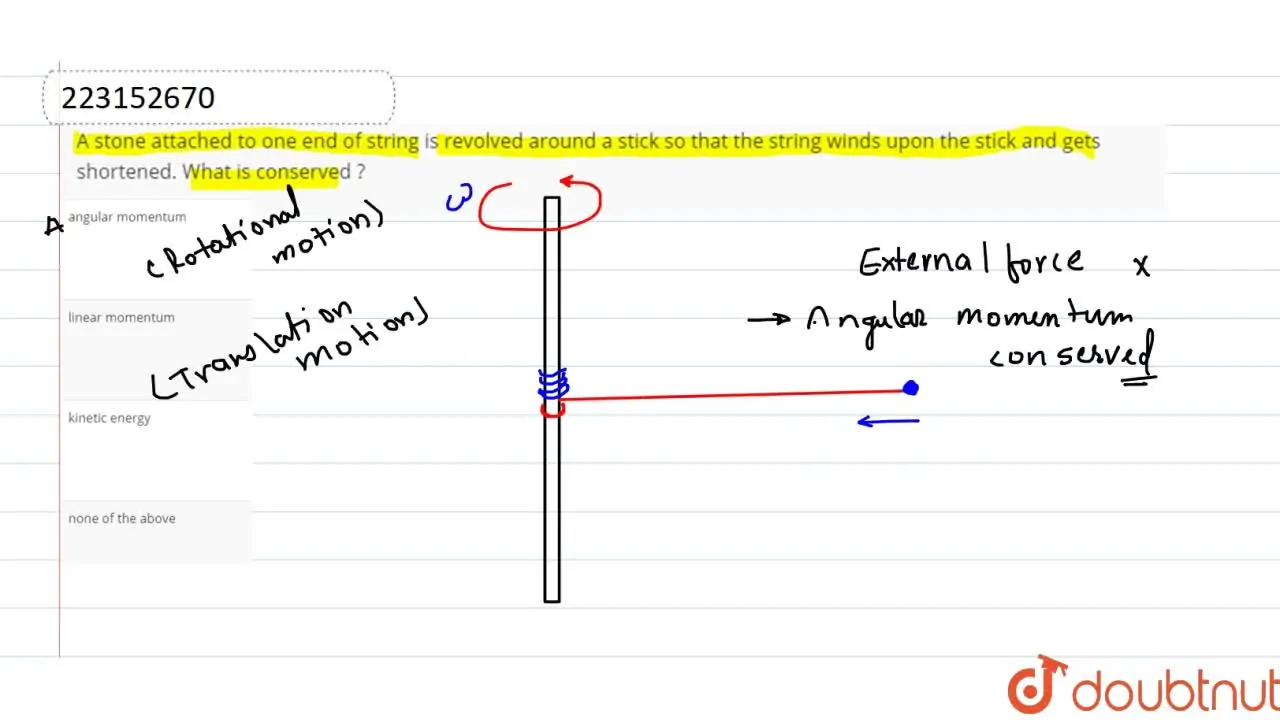
A stone attached to one end of string is revolved around a stick so that the string winds upon the stick and gets shortened. What is conserved ?
angular momentum
linear momentum
kinetic energy
none of the above
The correct Answer is:A
Step by step video, text & image solution for A stone attached to one end of string is revolved around a stick so that the string winds upon the stick and gets shortened. What is conserved ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 240videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-A )46videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 3 ( Section-B )24videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-438videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 334videos
SEMI CONDUCTOR AND LOGIC GATES
Similar Questions
A small body is attached to one end of a string is revolved around a rod so that the string winds upon the rod and get shortend. The quantity which is conserved is
View SolutionA stone is attached to one end of a string and rotated in a vertical circle . If the string breaks at the position of maximum tension , then it will break at
 View Solution
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical isView SolutionA stone is attached to one end of a string and rotated in a vertical circle . If the string breaks at the position of maximum tension , then it will break at
 View Solution
View SolutionIF a stone is tied to one end of the string and whirled in verticle circle, then the tension in the string at the lowest point is equal to
View SolutionA stone is tied to one end of a string and rotated in a vertical circle . What is the difference in tensions of the string at lowest and highest points of the vertical circle ?
View SolutionA stone tied to one end of rope and rotated in a circular motion . If the string suddenly breaks then the stone travels.
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
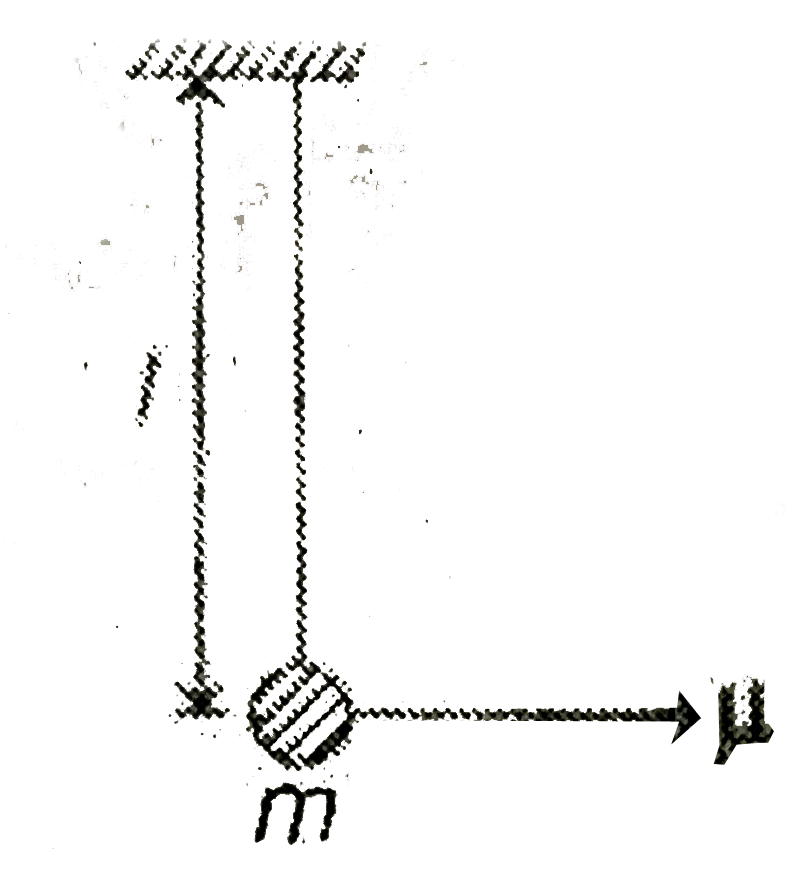
The tension in the string at an instant when acceleration of the particle is horizontal and √3g isView SolutionA stone tied to a string is rotated in a circle. If the string is cut, the stone flies away from the circle because
View SolutionA stone tied at the end of sring is whirled in a circle. If the string break , the stone flies away tangentially . Why ?
View Solution