The space between two coaxial cylinders, whose radii are a and b (where a<b as in (figure shown) is filled with a conducting medium . The specific conductivity of the medium is σ.
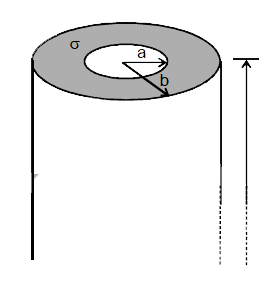
(a) Compute the resistance along the lenght of cylinder .
(b) Compute the resistance between the cylinders are very long as compared to their radii , i.e ., L>> b, where L is the lenght of the cylinders.
(a) R=ρlA=lσA=lσ(πb2−πa2)=lπσ(b2−a2)
(b) From Ohm's law , we have
→J=σ→E Assuming radial current density . →J becomes
→J=I2πrLˆr for a<r<b
and , therefore , " " →E=I2πσrLˆr
Here we have used the asssumption that L>>b so that →Eand→J are in cylindrically symmetric form. The potential drop across the medium is thus :
Vab=−∫ab→E(r).→dr=−I2πσL∫abdrr=I2πσLln(ba)
The resistance
Rab=VabI=In(ba)2πσL
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MOTIONChapter:CURRENT ELECTRICITYExercise:EXERCISE -1 (SECTION -A Definition of Current , Current Density , Drift Velocity )
Explore 8 Videos
- CURRENT ELECTRICITYBook:MOTIONChapter:CURRENT ELECTRICITYExercise:EXERCISE -1(SECTION B- Resistance & resistivity , Ohms law +VI (Volt - curr.) Characteristics + Colour Code + Temp . Dependence
Explore 8 Videos
- CURRENT ELECTRICITYBook:MOTIONChapter:CURRENT ELECTRICITYExercise:EXERCISE -3 SECTION -B (PREVIOUS YEAR PROBLEMS JEE MAIN)
Explore 42 Videos
- CONSTRAINED MOTION Book:MOTIONChapter:CONSTRAINED MOTION Exercise:EXAMPLES
Explore 12 Videos
- ELASTICITYBook:MOTIONChapter:ELASTICITYExercise:EXERCISE -3
Explore 60 Videos
Similar Questions
Knowledge Check
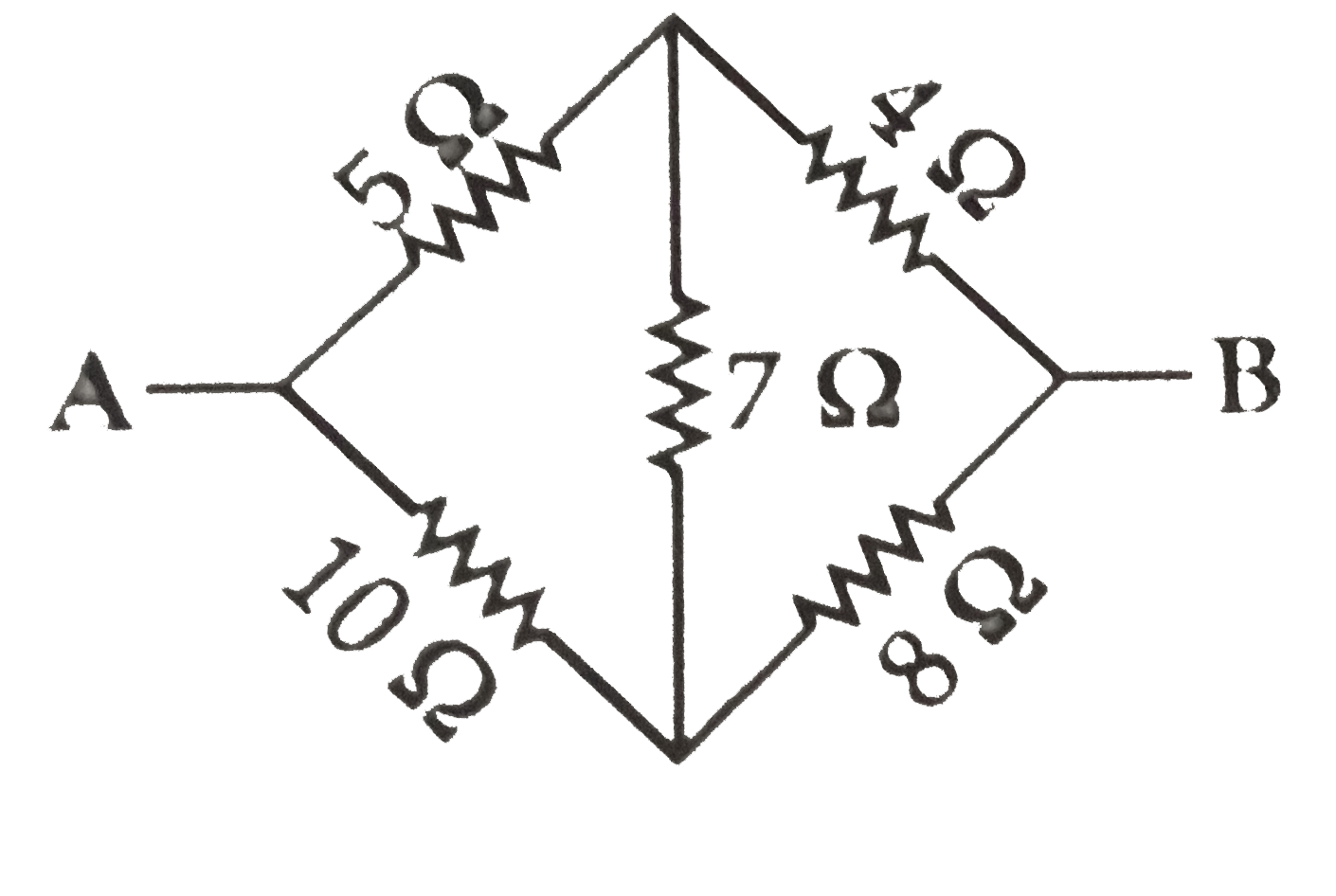
Each resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
 ArBr/4Cr/2D5r/8
ArBr/4Cr/2D5r/8Five resistances are connected as shown in the figure. The effective resistance between the points A and B is
 A103ΩB203ΩC15ΩD6Ω
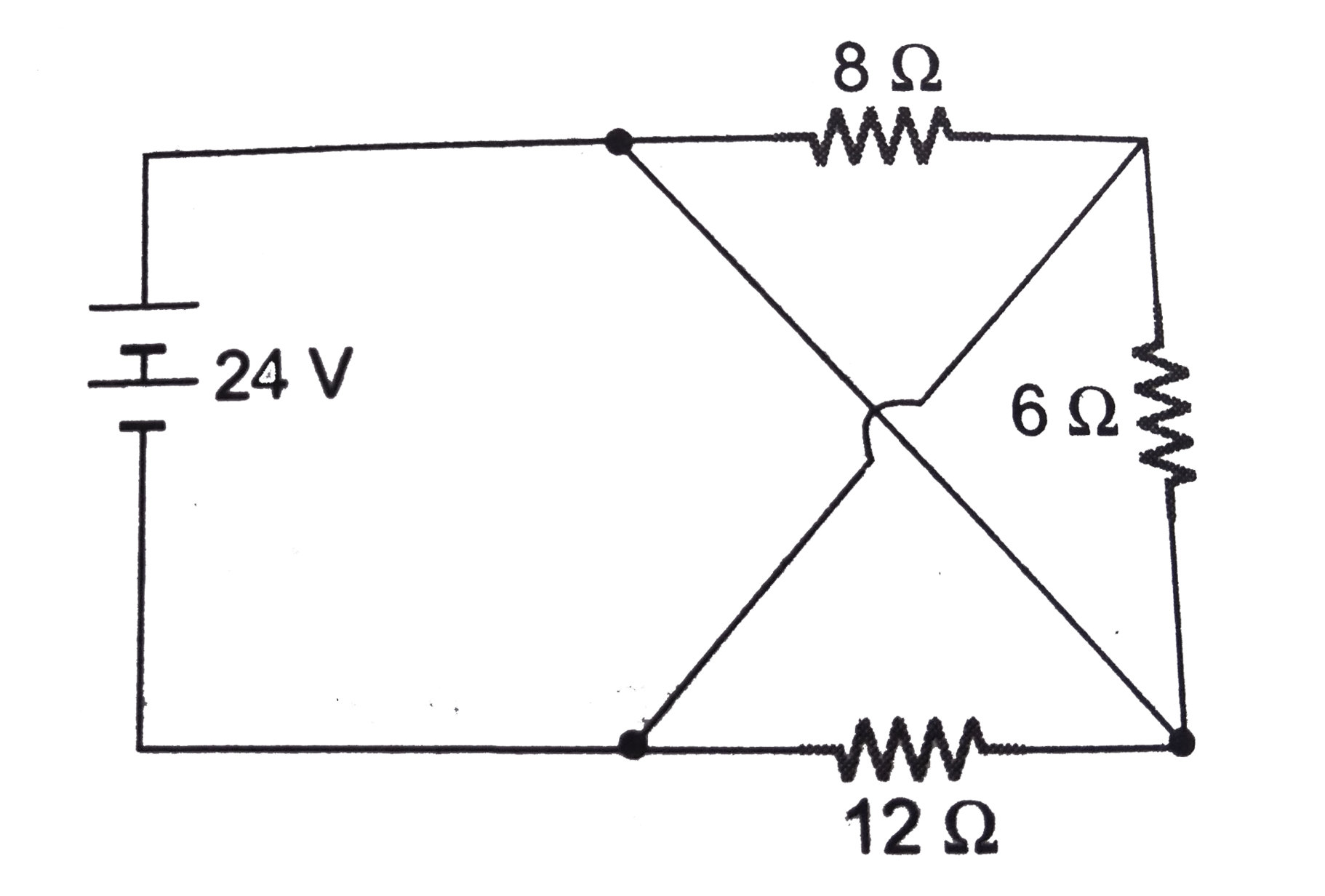
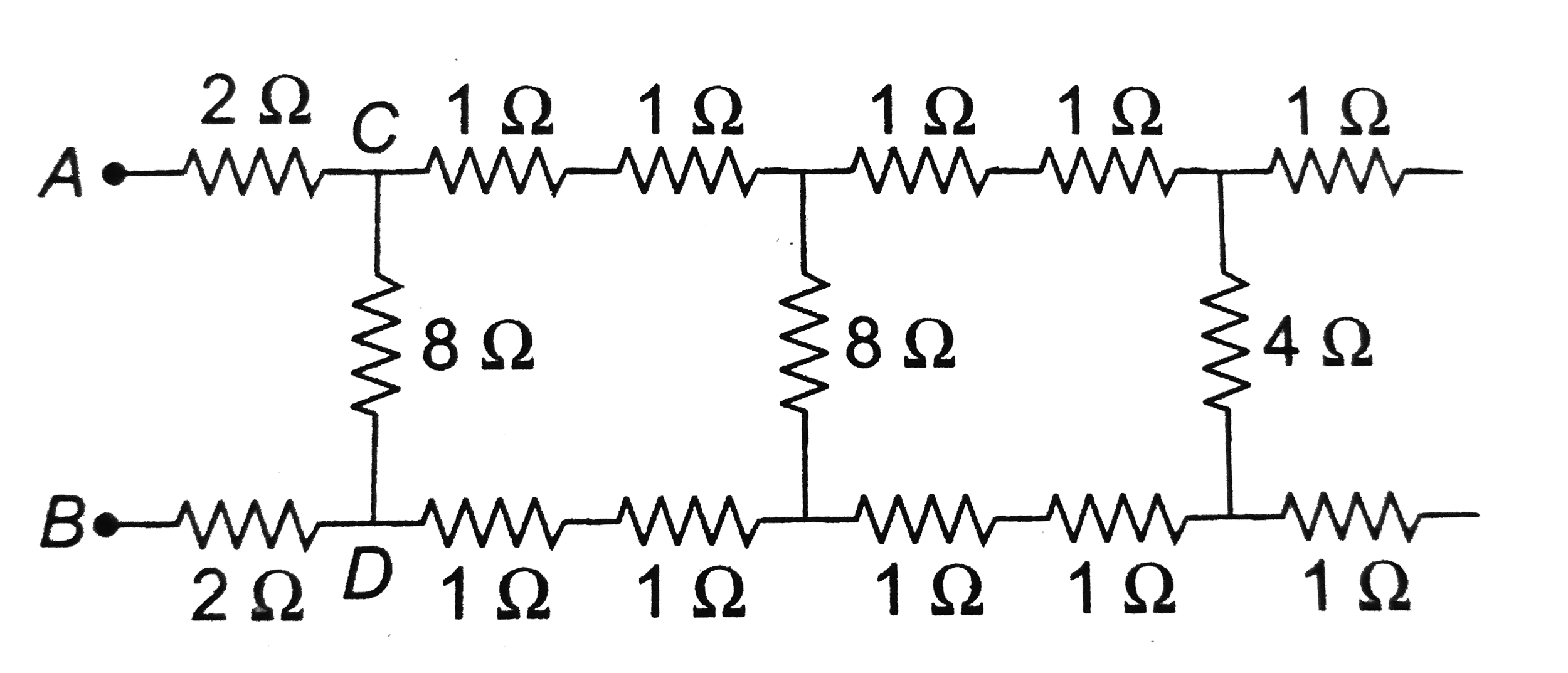
A103ΩB203ΩC15ΩD6ΩIn the figure shown, the total resistance between A and B is
 A50 AB2AC0.5AD109A
A50 AB2AC0.5AD109A
Compute total circuit resistance and battery current as shown in figure.
View SolutionThe space between two conducting concentric spheres of radii a and b(a<b) is filled up with homongeneous poorly conducting medium. The capacitance of such a system equals C. Find the resistivity of the medium if the potential difference between the spheres, when they are disconnected from an external voltage , decreases η-fold during the time interval Δt.
View SolutionThe space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
View SolutionIn the figure shown, the total resistance between A and B is
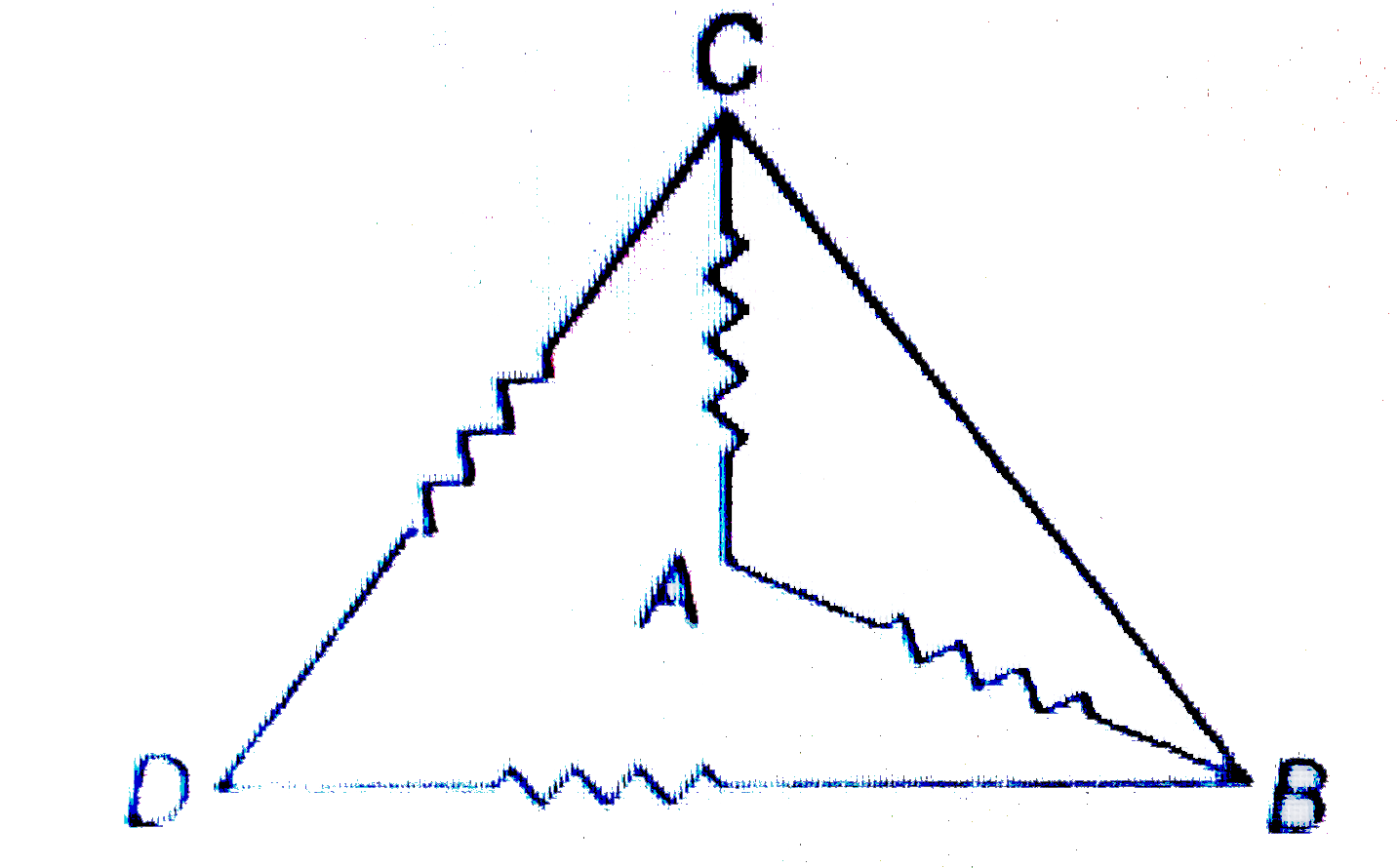
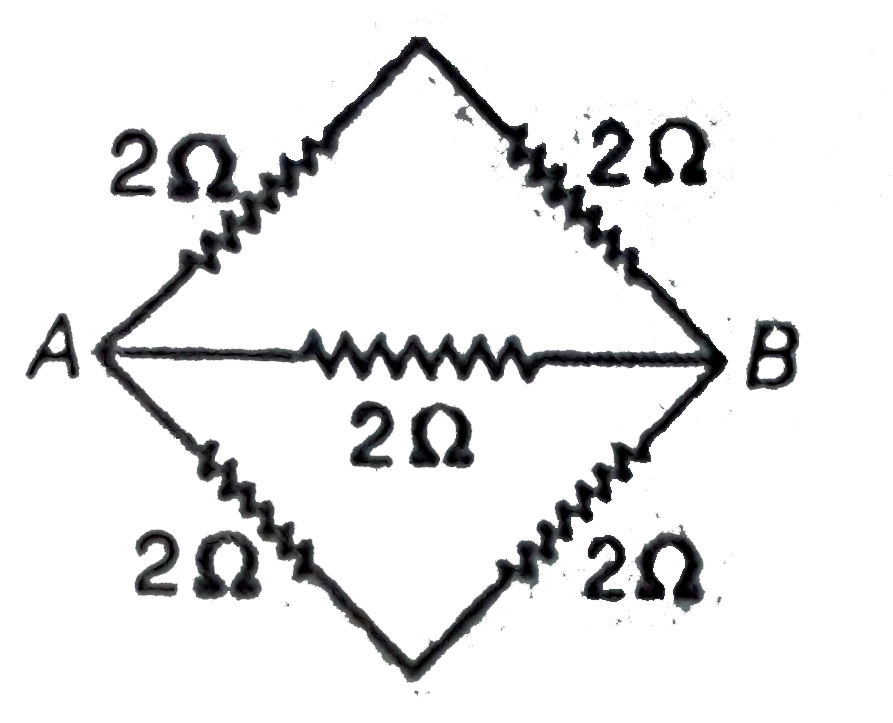
View SolutionEach resistance shown in figure is 2Ω. The equivalent resistance between A and B is
View Solution