Find the potential at point A
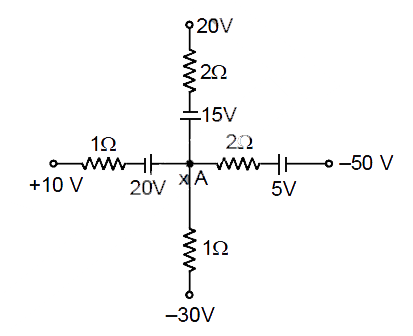
Let potential at A=x , applying kirchhoff current law at junction A
x−20−101+x−15−202+x−5+502+x+301=0
⇒2x−60+x−35+x+45+2x+602=0
⇒6x+10=0
⇒x=−53
Potential at A =−53V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -1 (SECTION -A Definition of Current , Current Density , Drift Velocity )
8 Videos
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -1(SECTION B- Resistance & resistivity , Ohms law +VI (Volt - curr.) Characteristics + Colour Code + Temp . Dependence
8 Videos
- CURRENT ELECTRICITYBOOK - MOTIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE -3 SECTION -B (PREVIOUS YEAR PROBLEMS JEE MAIN)
42 Videos
- CONSTRAINED MOTION BOOK - MOTIONCHAPTER - CONSTRAINED MOTION EXERCISE - EXAMPLES
12 Videos
- ELASTICITYBOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -3
60 Videos
Similar Questions
Knowledge Check
In the following circuit , find the potentials at points A and B is.
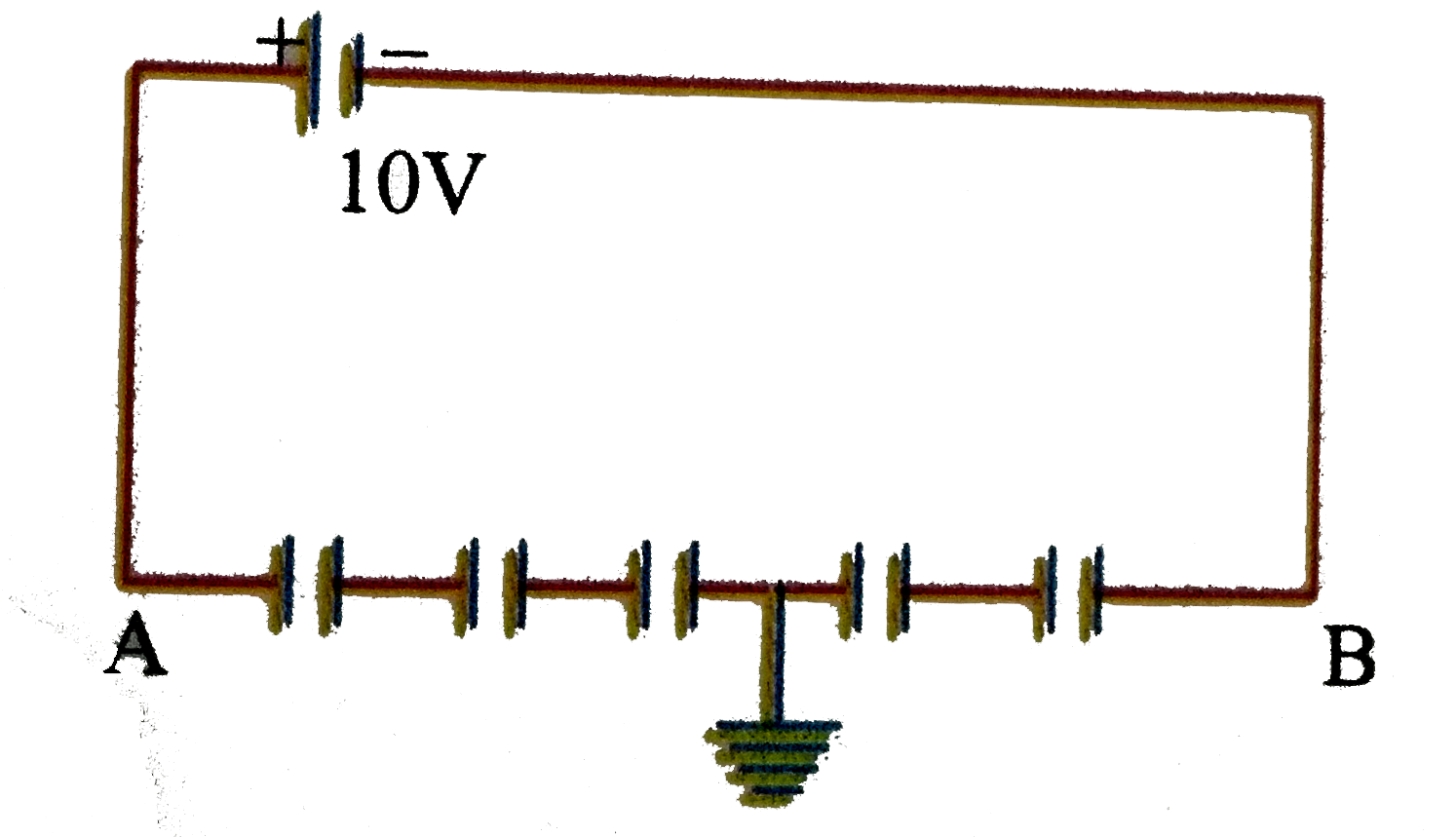 .A10 V,0VB6V,−4VC4V,−6VD5V,−5V
.A10 V,0VB6V,−4VC4V,−6VD5V,−5V
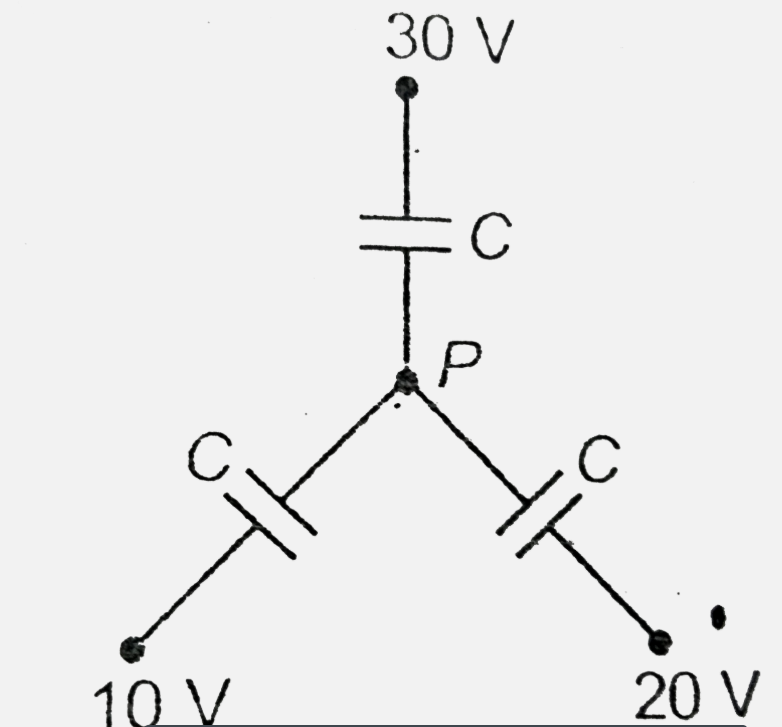
The arrangement shows a part of complete circuit. The potentials at point A and B are V1 and V2 respectively . Find the potential at point P.
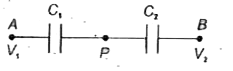
Strategy : The two capacitors C1 and C2 are connected in series . Therefore the charge on both of the capacitors is same . Let the potential at P is V .
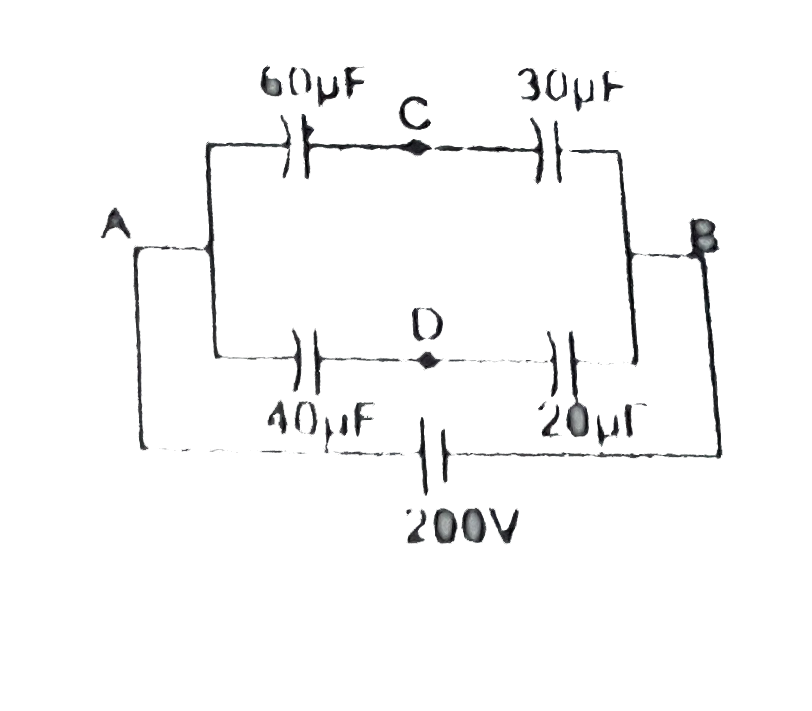
View SolutionTake the potential of the point B as shown in the figure to be 100 V.
(a) Find the potentials at the point c and D.
(b) If an uncharged capacitor is connected between C and D, then find the amount of charge that will appear on this capacitor
View SolutionThe gravitational field due to a mass distribution is given by →l=kx2ˆi, where k is a constant. Assuming the potential to be zero at infinity, find the potential at a point x = a.
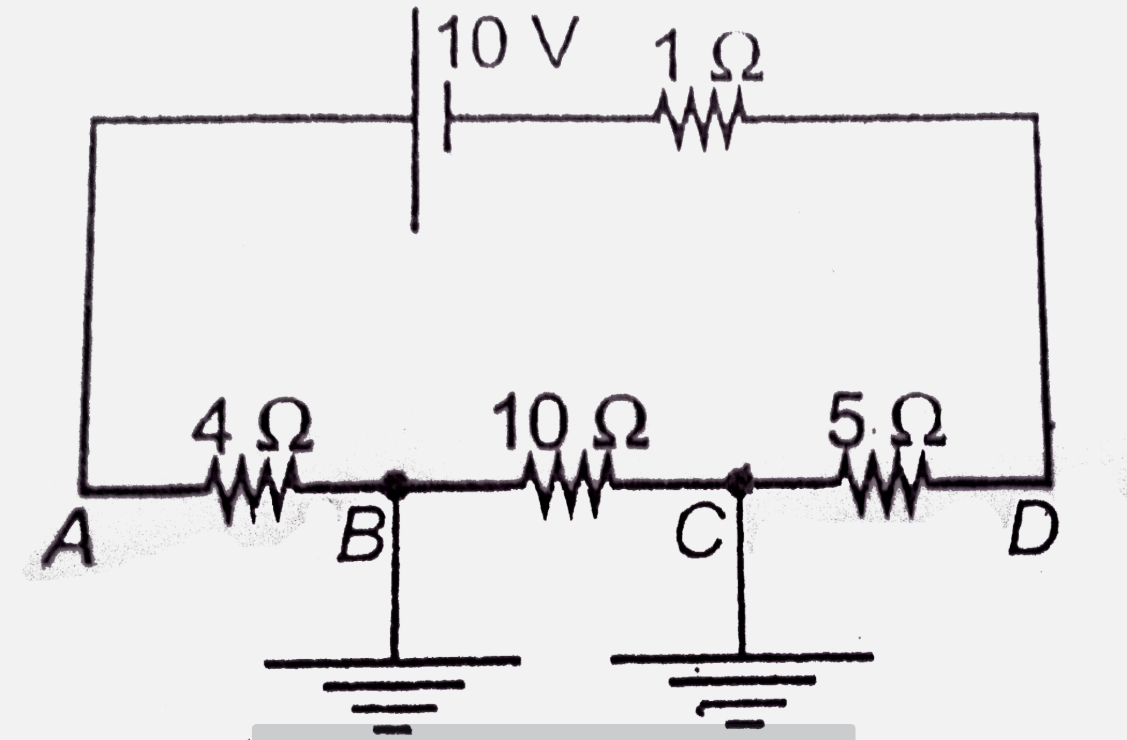
View SolutionIn the electrical circuit shown, points B and C are earthed . Find the potentials of points A and D .
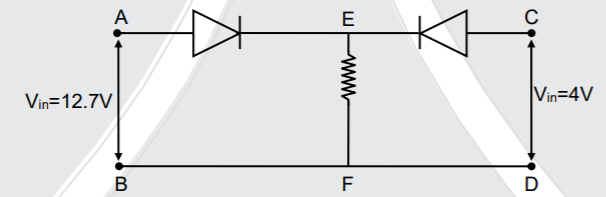
View SolutionIn the given circuit both diodes are ideal having zero forward resistance and built-in potential of 0.7 V. Find the potential of point E in volts.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionFind potential at point A and B due to the small charge -system fixed near origin. (distance between the charges is negligible).
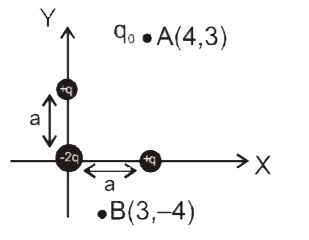
View Solution