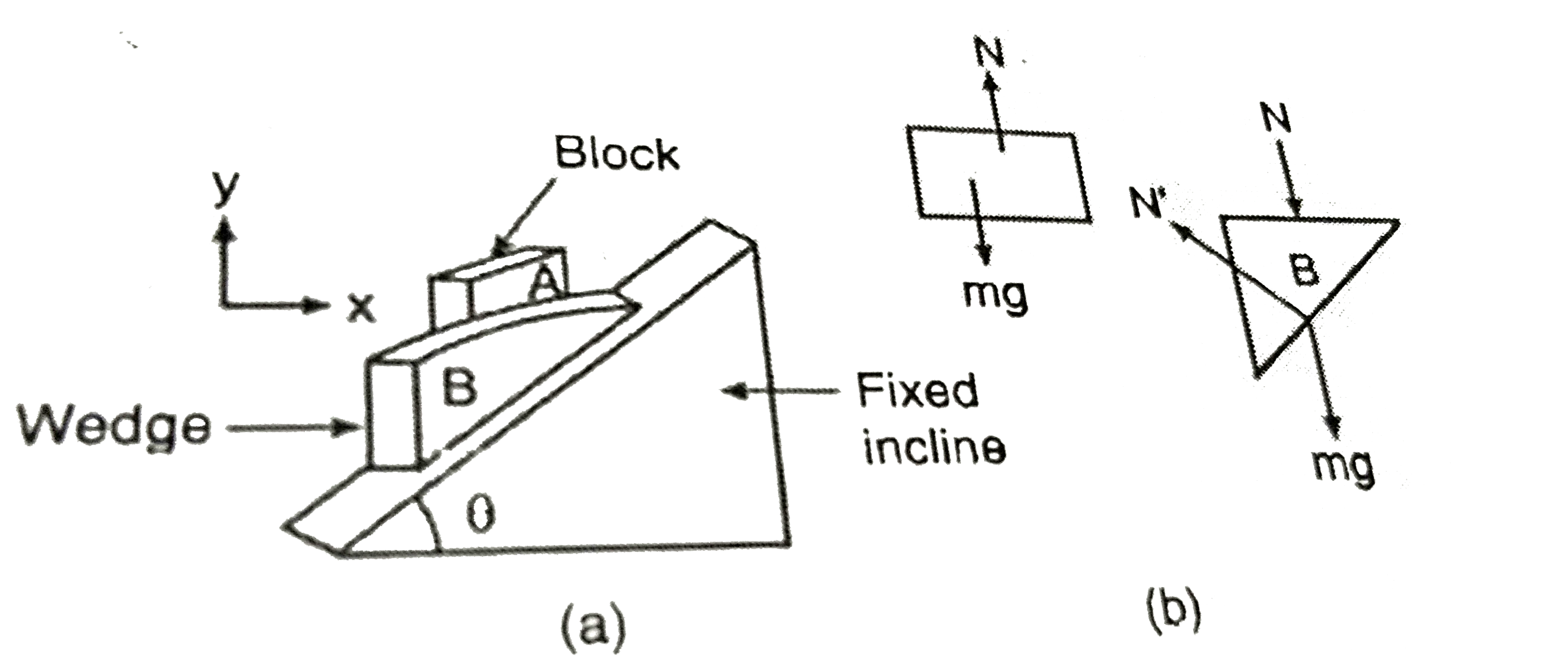
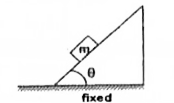
Block A of mass m is placed over a wedge of same mass m. Both the block and wedge are placed on a fixed inclined plane. Assuming all surfaces to be smooth, the displacement of the block A in ground frame in 1s is gsin2θx+sin2θ then the value of x is:
The correct Answer is:1
Let acceleration of wedge in ground frame is a down the plane. The acceleration of block A will be asinθ vertically downward
→aA/g=→aA/B+→aB/g....(i)
[aA/g]x=[aA/B]x+[aB/g]x......(ii)
From F.B.D. of A it is clear that Block A cannot accelerate horizontally i.e., in x-direction because there is no force in x-direction. Block A can accelerate in y-direction only. [aA/g]x=0 Therefore [aA/g]x=−[aB/g]x That means for an observation on wedge block moves only x>0
For block A: mg−N=m(asinθ) ....(iii)
For block B: (N+mg)sinθ=ma ....(iv)
On solving Eqns (iii) and (iv) we get
a=[2gsinθ1+sin2θ]
The acceleration of block A,
aA=asinθ=[2gsinθ1+sinθ]sinθ=[2gsin2θ1+sin2θ]
Displacement of block A in 1 s is
s=0+12aAt2
=12×[2gsin2θ1+sin2θ]×(1)2[gsin2θ1+sin2θ]
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Matrix match
7 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
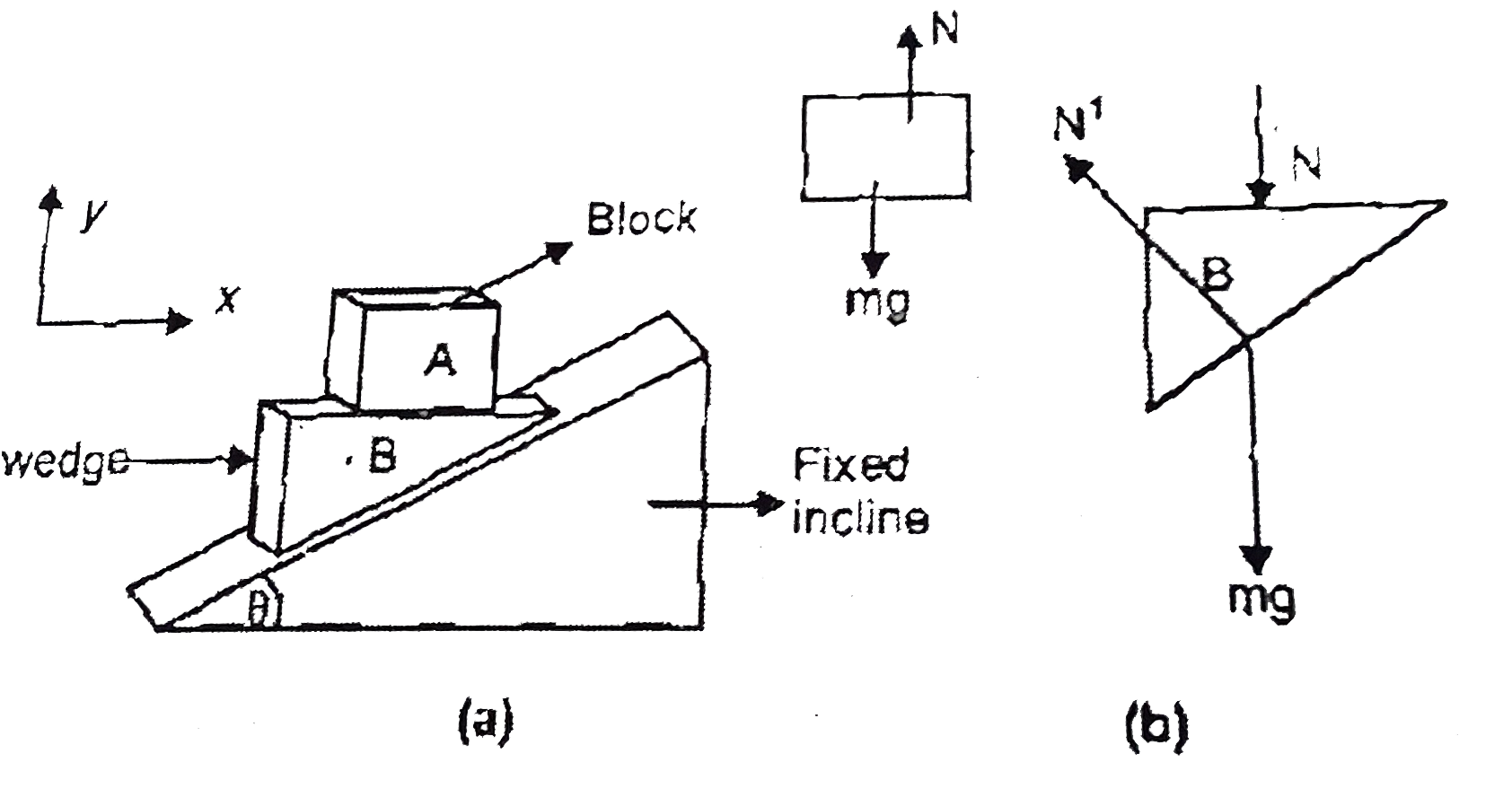
Block A of mass m is placed over a wedge of same mass m. Both the block and wedge are placed on a fixed inclined plane. Assuming all surfaces to be smooth calculate the displacement of the block A in ground frame in 1s.
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View Solution
Knowledge Check
a Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
 Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θA block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
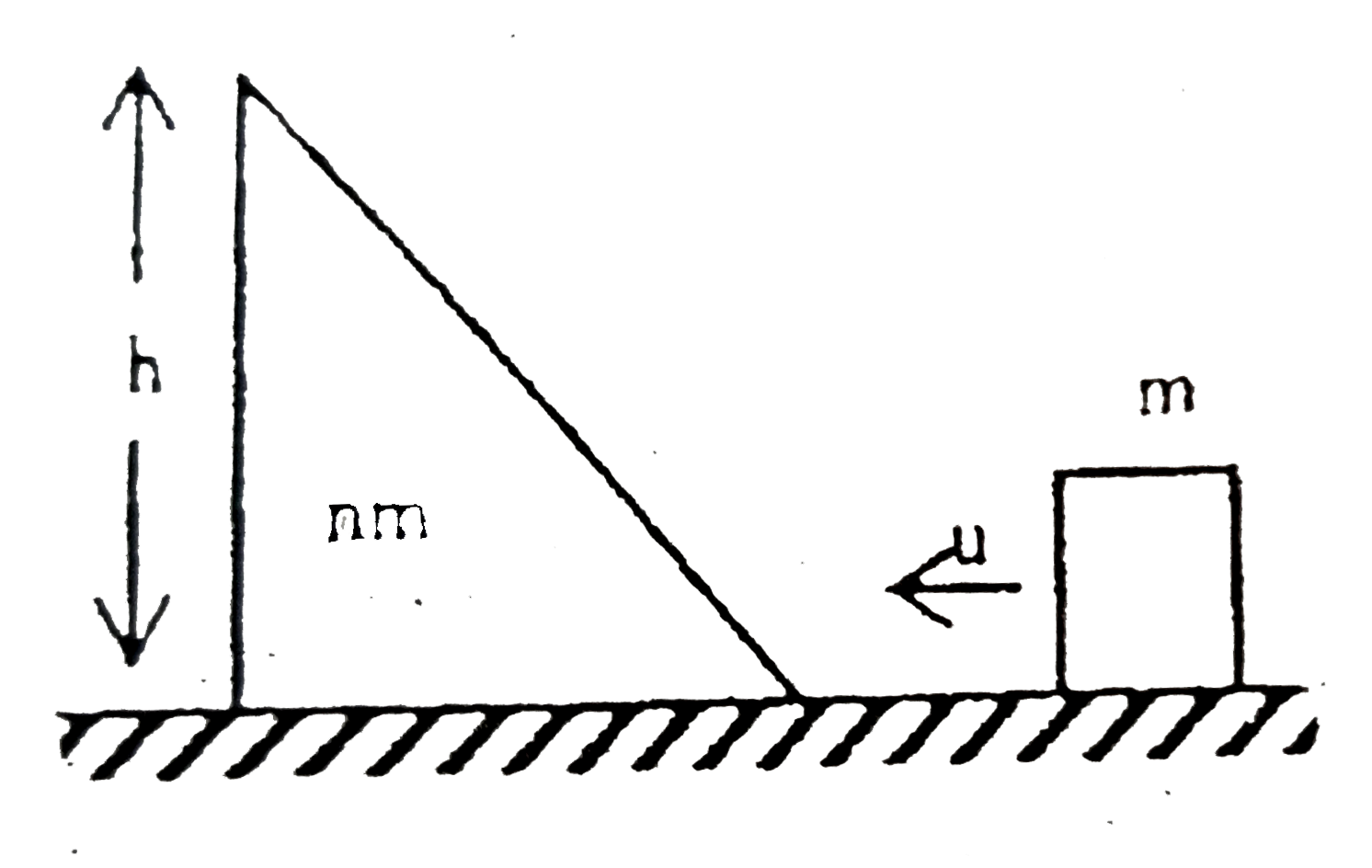 A√2ghBn2ghC√2gh(1+1n)D√2gh(1−1n)
A√2ghBn2ghC√2gh(1+1n)D√2gh(1−1n)A block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
 A√2ghB2nghC√2gh(1+1n)D√2gh(1−1n)
A√2ghB2nghC√2gh(1+1n)D√2gh(1−1n)
A block of mass m is at rest over the rough surface of the fixed wedge.

View SolutionA block of mass m is initially lying on a wedge of mass M with an angle of inclination θ as shown in figure. Calculate the displacement of the wedge when the block is released and reaches to the bottom of the wedge.

View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

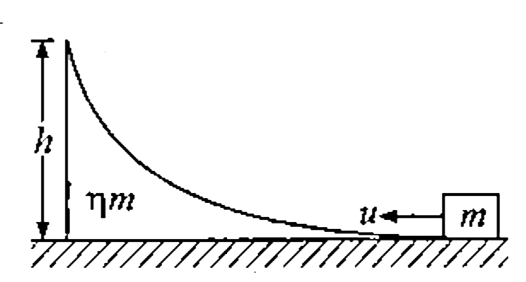
View SolutionA small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:
View SolutionA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
View Solution
