A uniform disk of radius r= 0.6 m and mass M = 2.5 kg is freely suspended from a horizontal pivot located a radial distance d = 0.30 m from its centre . Find the angular frequency of small amplitude oscillations of the disk .
The moment of inertia of the disk about a perpendicular axis passing through its centre is I=12mr2
Form the parallel axis theorem , the moment of inertia of the disk about the pivot point is
I'=I+Md2=2.5×0.6×0.62+2.5×0.30×0.30
=0.92+0.225
=0.45+0.225
=0.675kgm2
The angular frequency of small amplitude oscillations of a compound pendulum is given by
ω=√MgdI'=√2.5×9.8×0.300.675
=√7.350.675=√0.67510.9=3.3rads
Topper's Solved these Questions
- OSCILLATIONSBook:SURA PUBLICATIONChapter:OSCILLATIONSExercise:CREATIVE QUESTIONS (HOTS)
Explore 21 Videos
- OSCILLATIONSBook:SURA PUBLICATIONChapter:OSCILLATIONSExercise:VALUE BASED QUESTIONS
Explore 2 Videos
- OSCILLATIONSBook:SURA PUBLICATIONChapter:OSCILLATIONSExercise:NUMERICAL PROBLEMS (2 Marks)
Explore 5 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBook:SURA PUBLICATIONChapter:NATURE OF PHYSICAL WORLD AND MEASUREMENTExercise:ADDITIONAL QUESTIONS
Explore 241 Videos
- PROPERTIES OF MATTERBook:SURA PUBLICATIONChapter:PROPERTIES OF MATTERExercise:Value based Questions
Explore 5 Videos
Similar Questions
Knowledge Check
A unifrom solid disk of radius R and mass M is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .A4√Rg3B2√Rg3C√Rg3D3√Rg2
.A4√Rg3B2√Rg3C√Rg3D3√Rg2Two masses m1and m2 are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
A√Km2,m1gKB√Km1,m2gKC√Km2,m2gKD√Km1,m1gK
A ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View SolutionA uniform ring of radius 'R' is suspended from a horizontal nail 'A' as shown. Find time period of its small oscillations.

View SolutionTwo mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View Solution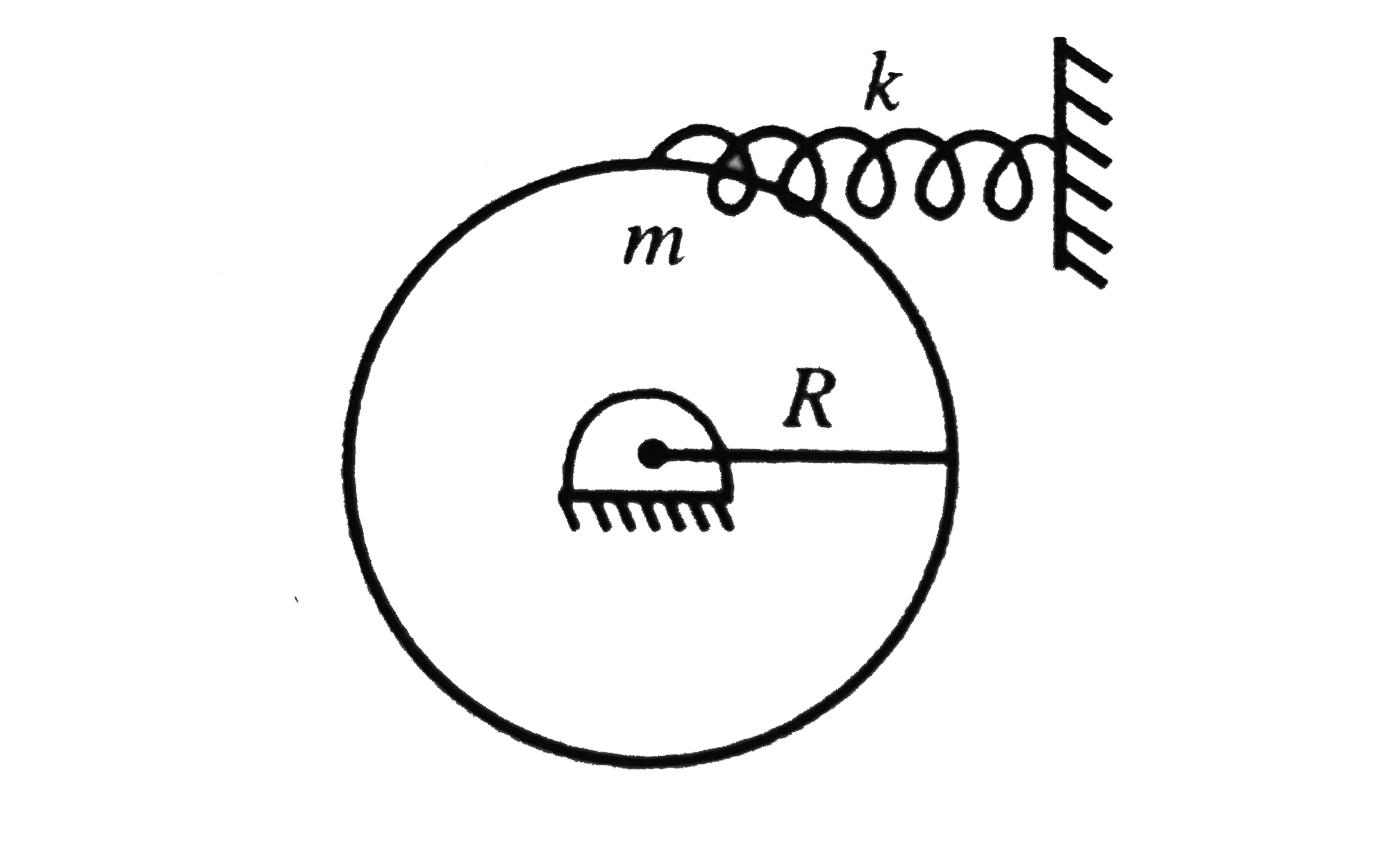
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View Solution

