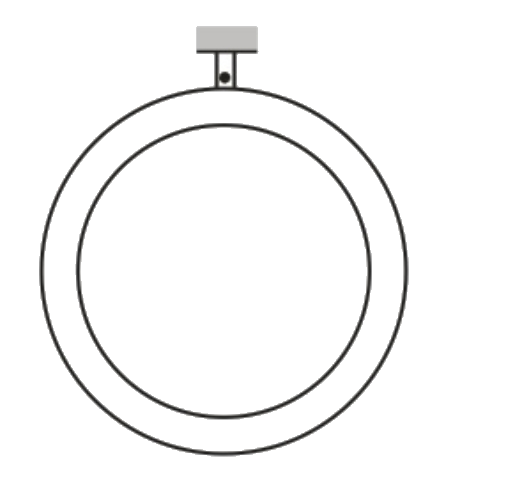
A ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

It is physical pendulum , the time period of which is ,
T=2π√Imgl
Here ,I=moment of ineria of the ring about point of suspension
mr2+mr2=2mr2
and l=distance of point of suspension from centre of gravity =r
∴T=2π√2mr2mgr=2π√2rg
∴ Angular frequency ω=2πT or ω=√g2r
Similar Questions
A ring of the radius r is suspended from a point on its circumference. If the ring is made to oscillate in the plane of the figure, then the angular frequency of these small oscillations is
View SolutionA uniform disc of radius R is pivoted at point O on its circumstances. The time period of small oscillations about an axis passing through O and perpendicular to plane of disc will be
View SolutionA uniform solid sphere of mass m and radius R is suspended in vertical plane from a point on its periphery. The time period of its oscillation is
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA uniform cylinder of mass m and radius R is in equilibrium on an inclined by the action of a light spring of stiffnesk, gravity and reaction force acting on it .If the angle of inclination of the plane is ϕ , find the angular frequency of small oscillation of the cylinder

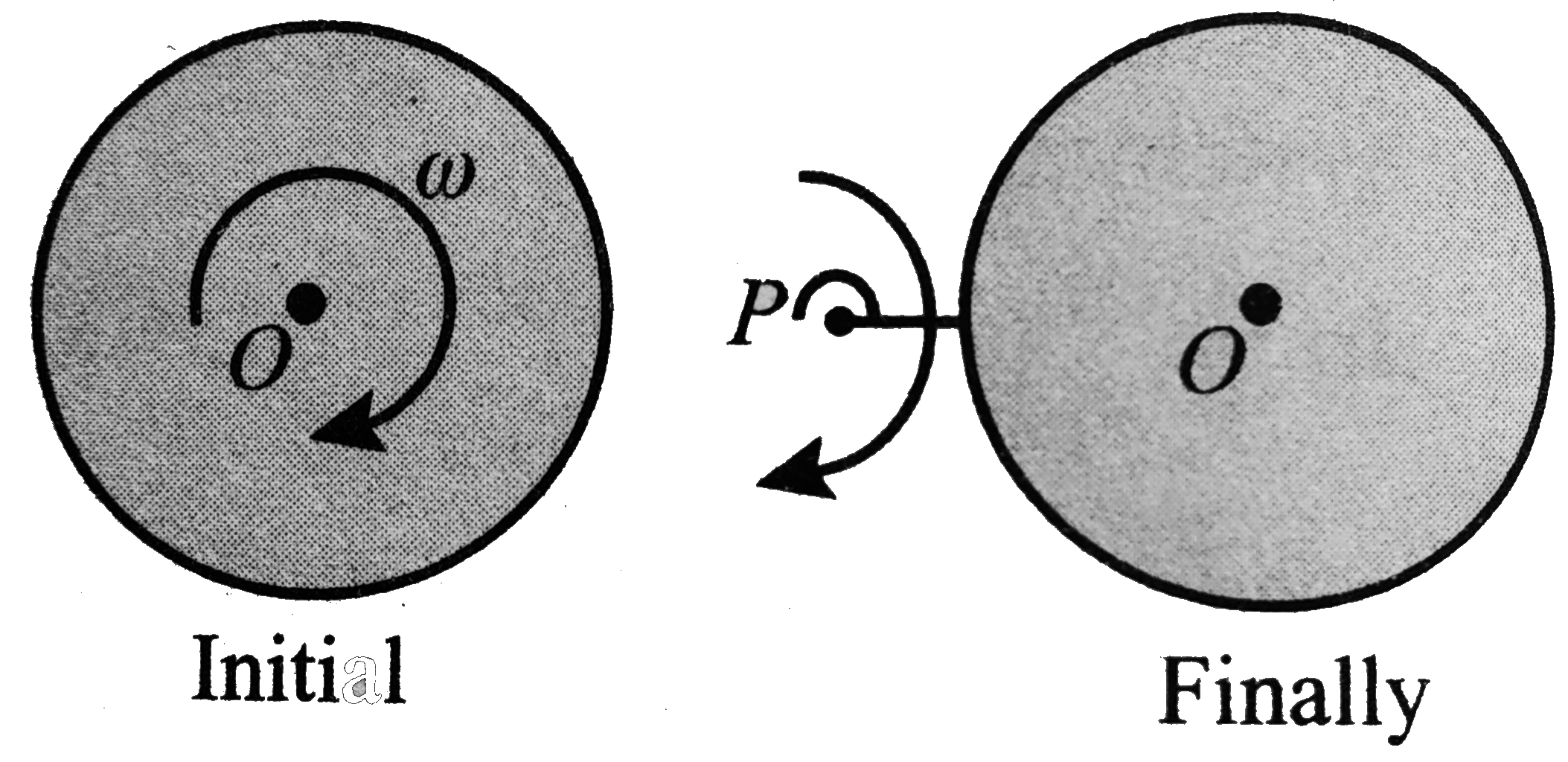
View SolutionA disc is freely rotating with an angular speed ω on a smooth horizontal plane. If it is hooked at a rigid pace P and rotates without bouncing about a point on its circumference. Its angular speed after the impact will be equal to.
View Solution
A metre stick swinging in vertical plane about a fixed horizontal axis passing through its one end undergoes small oscillation of frequency f0. If the bottom half of the stick were cut off, then its new frequency of small oscillation will become.
View SolutionFriction is absent everywhere and the threads, spring and pulleys are massless. If mA=mB=M, then the angular frequency of the system for small oscillations will be

View SolutionA circular ring of radius 5 cm is suspended horizontally from a point 12 cm vertically above its centre by 6 strings attached to its circumference at equal intervals. The cosine of the angle between two consecutive ring is
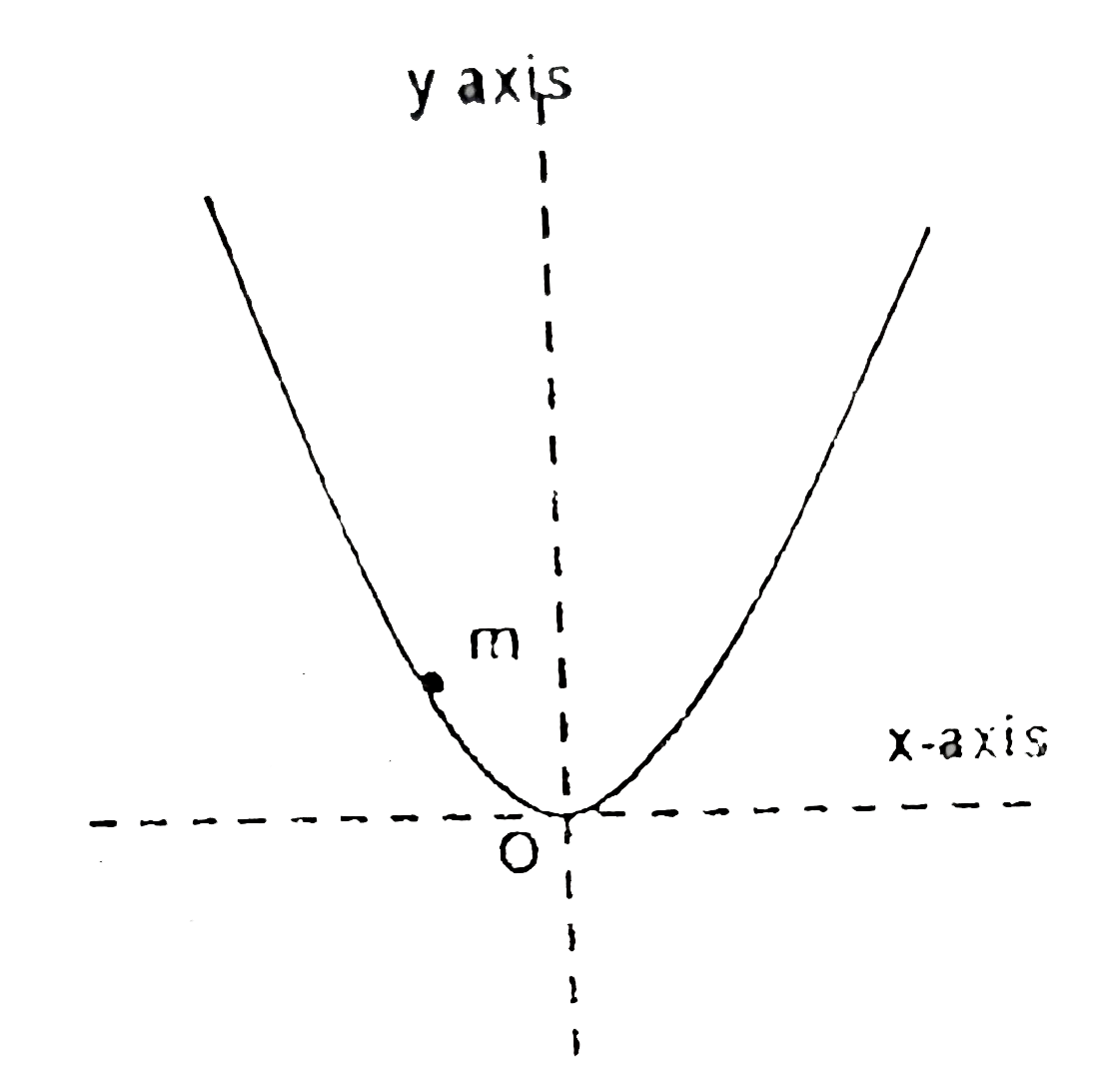
View SolutionA point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x2=ky then its angular frequency of oscillation is :
View Solution
