The relation between the numbers of pieces p Amy has learnt to sing at the end ofn weeks of singing lesson is given as : p = 2n + 3 .
After how many weeks would Amy be able to sing 17 pieces ?
The correct Answer is:7
To solve the problem step by step, we will follow the equation given and substitute the values accordingly.
Step 1: Understand the equation
The relation between the number of pieces p Amy has learned to sing after n weeks is given by the equation:
p=2n+3
Step 2: Substitute the known value
We need to find out after how many weeks Amy will be able to sing 17 pieces. Therefore, we substitute p=17 into the equation:
17=2n+3
Step 3: Isolate the term with n
To isolate n, we first subtract 3 from both sides of the equation:
17−3=2n
14=2n
Step 4: Solve for n
Next, we divide both sides by 2 to solve for n:
n=142
n=7
Conclusion
Amy will be able to sing 17 pieces after 7 weeks of singing lessons.
---
The relation between the number of pieces p Amy has learned to sing after n weeks is given by the equation:
p=2n+3
We need to find out after how many weeks Amy will be able to sing 17 pieces. Therefore, we substitute p=17 into the equation:
17=2n+3
To isolate n, we first subtract 3 from both sides of the equation:
17−3=2n
14=2n
Next, we divide both sides by 2 to solve for n:
n=142
n=7
Amy will be able to sing 17 pieces after 7 weeks of singing lessons.
Topper's Solved these Questions
Similar Questions
Give the correct order of initials T (true) or F (false) for following statements :-
(I) If an ion has 2 electrons in K shell, 8 electrons in I. Shell and 6 electrons in M shell, then number of S electrons present in that element is 6.
(II) The maximum number of electrons in a subshell is given by 2n2
(III) If electron has magnetic quantum number −1, then it cannot be present in s-orbital.
(IV) Only one radial node is present in 3p orbital.
View SolutionN is a two - digits number having sum of the digits as S and porduct of digits as P . How many such two -digit numbers exist such that 2N=2S+3P?
View Solution
Knowledge Check
A graduation cap is tossed upward . It is f feet above the ground s seconds after it has been thown . The relation ship between f and s is given by the equation f=60s−17s2, where 0≤s≤3.5 . How many feet above the ground is the cap 3 seconds after it is thrown ?
A27B41C60D80Was the Hoax a Hoax?
For an hour on the evening of October 30, 1938, Orson Welles and other performers from the Mercury Theatre flooded the airwaves with alarming “news bulletins” about a Martian invasion supposedly occurring in Grover’s Mill, New Jersey. They were performing a radio play adapted from The War of the Worlds, a science fiction novel by H. G. Wells. The next day, a front-page 34 headline in the New York Times declared–––––––––––––––––––––––––––––––––––––––––––––, “Radio Listeners in Panic, Taking War Drama as Fact.” 35 The Times article claimed that people had fled their homes and that police stations had been swamped with calls–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––. This version of events persisted, and the legend became that Welles’s broadcast had as many as twelve million people 36who feared–––––––––––– that Martians had invaded Earth.
Recently, however, scholars have questioned the accuracy of this legend, suggesting the degree of public hysteria has been grossly exaggerated. The authors of an article published in October 2013 go 37 so far–––––– to assign blame for the distortion to the newspaper industry 38 At this time–––––––––––––, Jefferson Pooley and Michael Socolow, both professors of communication studies, argue that the newspaper industry sought to discredit the newly emerging technology of radio, which was cutting into newspapers’ 39 profits. The newspaper industry tried to do this by portraying––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– the new medium as irresponsible
[1] Proof of ulterior motives is scarce,
40 consequently weakening Pooley and Socolow’s argument.–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– [2] For instance, the C. E. Hooper ratings indicate that a mere 2 percent of households had tuned in to the broadcast. [3] Pooley and Socolow also call into question the validity of an oft-cited report that was based on a survey conducted six weeks after the broadcast. [4] Just because some people found the broadcast unsettling, the authors contend, doesn’t mean they believed it and reacted with real terror. [5] According to this report, one million people indicated that they had been “frightened” by the broadcast. [6] Ratings, however, reveal that 41 far fewer than––––––––––––––– a million people had been listening to the broadcast. [7] Furthermore, Pooley and Socolow note that this survey conflated being ‘frightened,’ ‘disturbed,’ or ‘excited’ by the program with being ‘panicked.’” 42
Pooley and Socolow describe a more likely scenario: most people who heard the broadcast understood they were listening to a piece of fiction, but 43 some being–––––––––––– influenced by the sensationalized news coverage afterward, later “remembered” being more afraid than they had been. The researchers also suggest that, 44 not unlike––––––––––– people who got caught up in the excitement of the story when reading about it in the newspaper, the American public may have been willing to embrace the legend because of its appeal to the imagination.
The writer wants to add a supporting detail to indicate that the story was widely reported. Which choice best accomplishes this goal?ANO CHANGEBOther newspapers also ran stories claiming that the broadcast had incited mass hysteria.CIn 2013, many newspapers and magazines featured articles about the seventy‑fifth anniversary of the broadcastDThe Times was then and is now one of the United States’ most popular news sources
A botanist is cultivating a rare species of plant in a controlled environment and currently has 3000 of these plants. The population of this species that the botanist expects to grow next year, Nnext year, can be estimated from the number of plants this year, Nthis year, by the equation below.
Nnext year=Nthis year+0.2(Nthis year)(1−Nthis yearK)
The constant K in this formula is the number of plants the environment is able to support.
The botanist would like to increase the number of plants that the environment can support so that the population of the species will increase more rapidly. If the botanist’s goal is that the number of plants will increase from 3000 this year to 3360 next year, how many plants must the modified environment support?
View SolutionA ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a transparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2 ,where k=1.0m−3/2.the refractive index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.
View SolutionA company uses three machines to manufacture two types of shirts, half sleeves and full sleeves. The number of hours required per week on machine M1,M2andM3 for one shirt of each type is given in the following table :
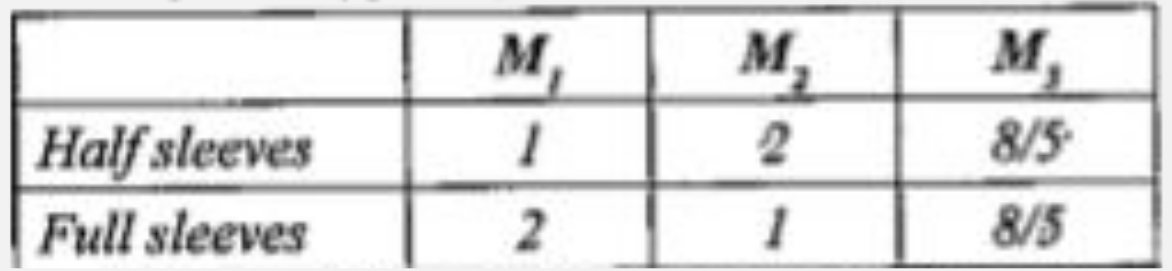
None of the machines can be in operation for more than 40 hours per week. The profit on each half sleeve shirt is Rs 1 and the profit on each full sleeve shirt is Rs 1.50. How many of each type of shirts should be made per week to maximize the company's profit ?
View Solutionvan der Waal's equation for calculating the pressure of a non ideal gas is
(P+an2V2)(V−nb)=nRT
van der Waal's suggested that the pressure exerted by an ideal gas , Pideal, is related to the experiventally measured pressure, Pideal by the equation
Pideal=Preal↑observed pressure+an2V2↑currection term
Constant 'a' is measure of intermolecular interaction between gaseous molecules that gives rise to nonideal behavior. It depends upon how frequently any two molecules approach each other closely. Another correction concerns the volume occupied by the gas molecules. In the ideal gas equation, V represents the volume of the container. However, each molecule does occupy a finite, although small, intrinsic volume, so the effective volume of the gas vecomes (V-nb), where n is the number of moles of the gas and b is a constant. The term nb represents the volume occupied by gas particles present in n moles of the gas .
Having taken into account the corrections for pressure and volume, we can rewrite the ideal gas equation as follows :
(P+an2V2)corrected pressure(V−nb)corrected volume=nRT
AT relatively high pressures, the van der Waals' equation of state reduces to
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19 C.
Q. The allowed energy for the particle for a particular value of n is proportional to
View SolutionWhen a particle is restricted to move along x-axis between x=0 and x=a, where α if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x=0 and x=a. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as E=p22m. Thus the energy of the particle can be denoted by a quantum number n taking values 1,2,3, ...(n=1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from x=0 to x=α. Take h=6.6×10−34Js and e=1.6×10−19C
Q. The speed of the particle that can take discrete values is proportional to
View Solution
