A ray of light travelling in air is incident at grazing angle (incident angle=90∘) on a long rectangular slab of a transparent medium of thickness t=1.0 (see figure). The point of incidence is the origin A(O,O) .The medium has a variable index of refraction n(y) given by :n(y)=[ky3/2+1]1/2 ,where k=1.0m−3/2.the refractive index of air is 1.0<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_RO_C01_E01_029_Q01.pngwh=80%mx-autosty≤=background:white;><br>(i)Obta∈arelationbetweentheslopeofthetrajec→ryoftherayatap∮B(x,y)∈themediumandthe∈cnt∠attˆp∮<br>(ii)obta∈anequationforthetrajec→ryy(x)oftheray∈themedium.<br>(ii)Determinethec∞rd∈ates(x_(1),y_(1))ofthep∮P.where the ray the ray intersects upper surface of the slab -air boundary.
Indicate the path of the ray subsequently.
a. If i is the angle of incidence at B(x,y), then slope of trajectory at B,
dy/dx=tanθ=tan(90∘−i)=coti (i)
b. From Snell's law, nsini=constantC.
From Snell's law at A(0,0) ,
nsini=1×sin90∘=1⇒nsini=1
sini=1/n or i=sin−1(1/n)
∴coti=cosisini=√(1−1/n)21/n=√n2−1
From Equ. (i),
or n2sin2i or n211+cot2i=1
or n21+(dy/dx)2=1
Given n=[ky3/2+1]1/2⇒n2=ky3/2+1
∴ky3/2+11+(dy/dx)2=1⇒ky3/2+1=1+(dydx)2
or (dy/dx)2=ky3/2⇒dy/dx−k1/2y3/4
or dy/y3/4=k1/2dx.
Integrating, we get 4y1/4=k1/2x+C
where c is constant of integration.
At x=0,y=0⇒C=0.
∴4y1/4=k1/2x
As k=1.0 (given)
∴y1/4(1/4)x (iii)
This is the required equation of trajectory.
c. At y=1.0 m, Eq. (ii) gives x=4m.
∴B(x1,y1)=P(4,1)
d. The path of the ray subsequently will be the grazing angle of emergence since
nsine=1 or 1sine=1⇒e=90.

Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.2
20 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
Knowledge Check
The refractive index of a medium is √3. What is the angle of refraction, if unpolarizing light is incident on the polarising angle of the medium ?
A60∘B45∘C30∘D0∘
A ray of light is incident perpendicularly on a glass slab. The angle of incidence is 900.
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light travelling in air is incident at grazing incidence on a slab with variable refractive index, n (y)=[ky3/2+1]1/2 where k=1m−3/2 and follows path as shown in the figure. What is the total deviation produced by slab when the ray comes out.

View SolutionA ray of light travelling in air is inciden at angle of inciden 30∘ on one surface of slab in which refractive index varies with y. The light travels along the curve y=4x2 ( y and x are in meter) in the slab. Find out the refractive index of the slab at y=1/2m in the slab.

View SolutionLight travelling in air falls at an incidence angle of 2∘ on one rafracting surface of a prism of refractive index 1.5 and angle of refraction 4∘. The medium on the other side is water (n=4/3) . Find the deviation produced by the prism.
View SolutionA ray of light is incident on a transparent medium at polarizing angle. What is the angle between the reflected ray and the refracted ray .
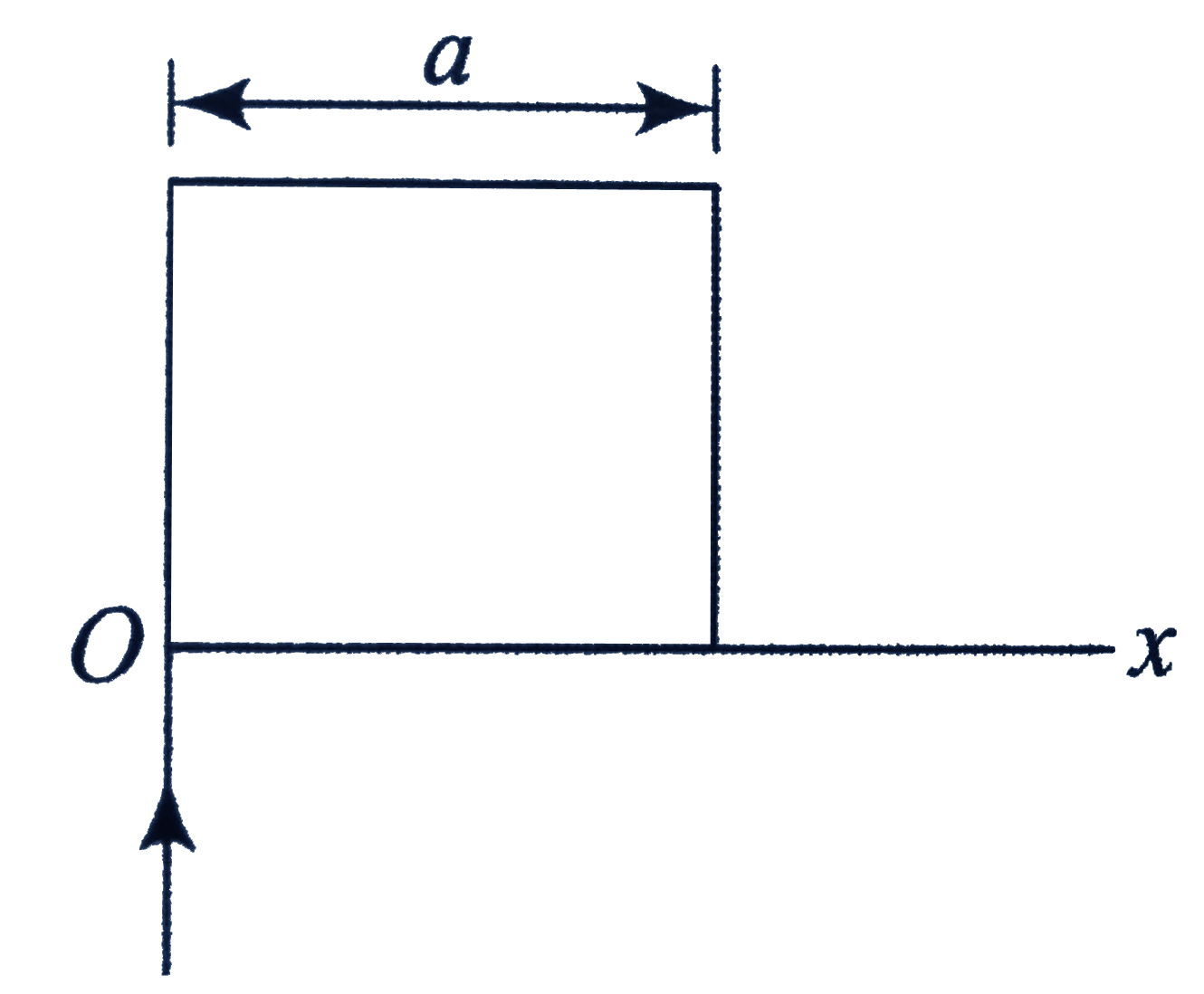
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View Solution