A thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.
Let f1 be the focal length of convex lens, radius of curvature of each curved face is R.
1f1=(m−1){1R−(1−R)}=(μ−1)2R
⇒f1=R2(μ−1)=R2(32−1)=R
When the space between the lens and mirror is filled by water of refractive index μ1=4/3 then the focal length of liquid concave lens f2 is
1f2=(μ1−1)(−1R−∞)
⇒f2=−Rμ1−1=−R(43−1)=−3R
The combined focal length of lenses if F1=15cm
∴1F=1f1+1f2⇒115=1R−13R=3−13R
3R=30⇒R=10cm
In the second case,
F2=25cm,Letμ1=μ2.
∴1F2=1f1+1f2⇒125=110+1f′2
⇒1f′2=125−110=2−550
∴f′2=−503cm
f'′2=Rμ2−1⇒μ2−1=−Rf′2=−10(−50/3)=35=0.6
⇒μ2=1+0.6=1.6

Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Exercise1.1
Explore 14 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Exercise1.2
Explore 20 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Integer Type
Explore 4 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
Similar Questions
A thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. The radius of curvature of the convex surface is
View SolutionAn equiconvex lens of refractive index n2 is placed such that the refractive index of the surrouding media is as shown. The lens :
View SolutionA thin bi-convex lens made up of glass of refractive index 3/2 is placed is front of a plane mirror. The space between the lens and the mirror is filled with water of refractive index 4/3 . The radii of curvatures of the lens are R1=15cm and R2=25cm . A point object is placed at distance x from the surface whose curvature is R1. The distance x is greater than the separation between the lens and the mirror. Find the value of x so that image must coincide with the object.
View SolutionOn a horizontal plane mirror, a thin equiconvex lens of glass is placed and when the space between the lens and mirror is filled with a liquid, an object held at a distance D which is 30cm vertically above the lens is found to coincide with its own image as shown in Figure. If equiconvex lens of glass has refractive index μ=1.5 and radius of curvature R=20cm then find refractive index of the liquid.

View SolutionA small object is kept at 18cm from combination of a convex lens and plane mirror to get the image on object itself. Now the space between lens and mirror is filled with liquid of refractive index μL. Now we need to keep the object at 27cm to get the image on object. Find μL.
_2019_CBT4_E01_078_Q01.png)
View SolutionA convex lens of refractive index 3/2 has a power of 2.5∘. If it is placed in a liqud of refractive index 2,the new power of the lens is
View SolutionA biconvex lens of focal length 15cm is in front of a plane mirror. The distance between the lens and the mirror is 10cm. A small object is kept at distance of 30cm from the lens. The final image is
View Solution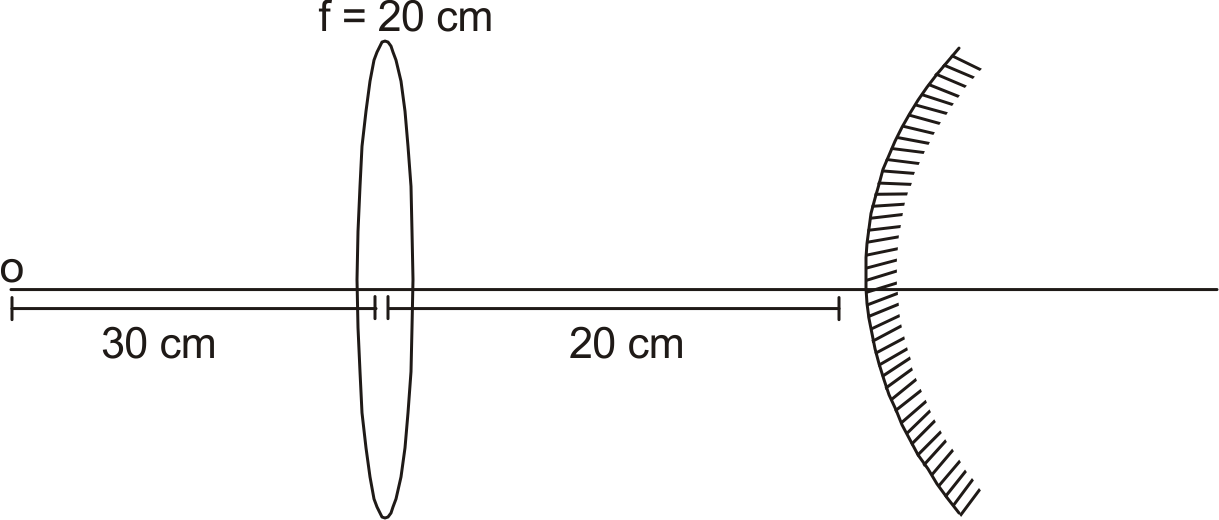
The lens shown is equiconvex having refractive Index. 1.5. In the situation shown the final image of object coincides with the object. The region between lens and mirror is now filled with a liquid of Rrefractive Index 2. Then find the separation between O & image formed by convex mirror.
View SolutionA double convex thin lens made of glass of refractive index 1.6 has radii of curvature 15 cm each. The focal length of this lens when immersed in a liquid of refractive index 1.63 is :
View SolutionA double convex lens of refractive index m1 is immersed in a liquid of refractive index m2. This lens will act as:
View Solution