A model of a planned city is made where ans actual distance 10 miles is represented as 5 meters. If the area of the city is 60 square, and 1 mile = 1600 meters, what is the area of the model in square miles ?
5.9×104 square miles
5.9×10−5 square miles
5.9×10−6 square miles
5.9×10−7 square miles
The correct Answer is:C
To solve the problem step-by-step, we need to determine the area of the model city in square miles based on the given information.
Step 1: Understand the Scale
We know that 10 miles in reality is represented as 5 meters in the model. Therefore, we can find the scale of the model:
Scale=5 meters10 miles=12 meters per mile
Hint: To find the scale, divide the model distance by the actual distance.
Step 2: Calculate the Area of the Model
The area of the actual city is given as 60 square miles. To convert this area into square meters, we need to convert miles to meters. Since 1 mile = 1600 meters, we can express the area in square meters:
Area in square meters=60 miles2×(1600 meters/mile)2
Calculating this gives:
=60×16002 square meters
Hint: When converting area, remember to square the conversion factor.
Step 3: Calculate the Area in the Model
Now, using the scale we found earlier, we can find the area of the model. Since 1 mile is represented as 0.5 meters, we can express the area in the model as:
Area of the model=Area of the city×(1 meter0.5 meters)2
Calculating this gives:
=60×(10.5)2=60×4=240 square meters
Hint: When converting area, remember to square the scale factor.
Step 4: Convert Area from Square Meters to Square Miles
Now we need to convert the area from square meters back to square miles. We know that:
1 mile=1600 meters⟹1 square mile=(1600 meters)2=2560000 square meters
To convert the area of the model from square meters to square miles:
Area in square miles=240 square meters2560000 square meters/square mile
Calculating this gives:
=2402560000≈0.00009375 square miles
Hint: To convert from square meters to square miles, divide by the number of square meters in one square mile.
Final Result
Thus, the area of the model in square miles is approximately:
0.00009375 square miles
We know that 10 miles in reality is represented as 5 meters in the model. Therefore, we can find the scale of the model:
Scale=5 meters10 miles=12 meters per mile
Hint: To find the scale, divide the model distance by the actual distance.
The area of the actual city is given as 60 square miles. To convert this area into square meters, we need to convert miles to meters. Since 1 mile = 1600 meters, we can express the area in square meters:
Area in square meters=60 miles2×(1600 meters/mile)2
Calculating this gives:
=60×16002 square meters
Hint: When converting area, remember to square the conversion factor.
Now, using the scale we found earlier, we can find the area of the model. Since 1 mile is represented as 0.5 meters, we can express the area in the model as:
Area of the model=Area of the city×(1 meter0.5 meters)2
Calculating this gives:
=60×(10.5)2=60×4=240 square meters
Hint: When converting area, remember to square the scale factor.
Now we need to convert the area from square meters back to square miles. We know that:
1 mile=1600 meters⟹1 square mile=(1600 meters)2=2560000 square meters
To convert the area of the model from square meters to square miles:
Area in square miles=240 square meters2560000 square meters/square mile
Calculating this gives:
=2402560000≈0.00009375 square miles
Hint: To convert from square meters to square miles, divide by the number of square meters in one square mile.
Thus, the area of the model in square miles is approximately:
0.00009375 square miles
Topper's Solved these Questions
Similar Questions
A rectangular solid has square base, with each side of the base measuring 4 meters. If the volume of the solid is 112 cubic meters, what is the surface area of the solid?
View SolutionOn a certain map, 1 inch represents 2 kilometers. A region is located on the map that is 1.5 inches by 4.0 inches. What is the actual area of the region in square miles if 1 kilometer is equal to 0.6 mile?
View Solution
Knowledge Check
A rectangle has a perimeter of 16 meters and an area of 15 square meters. What is the longest of the side lengths, in meters, of the rectangle?
A3B5C10D15On the certain map, 1.5 inches represents a distance of 120 miles. If two cities on this map are 1 foot apart, what is the distance, in miles, between the cities?
A180B480C960D1,080Stacy has 30 meters of fencing that she wishes to use to enclose a rectangular garden. If all of the fencing is used, what is the maximum area of the garden, in square meters, that can be enclosed?
A48.75B56.25C60.50D168.75
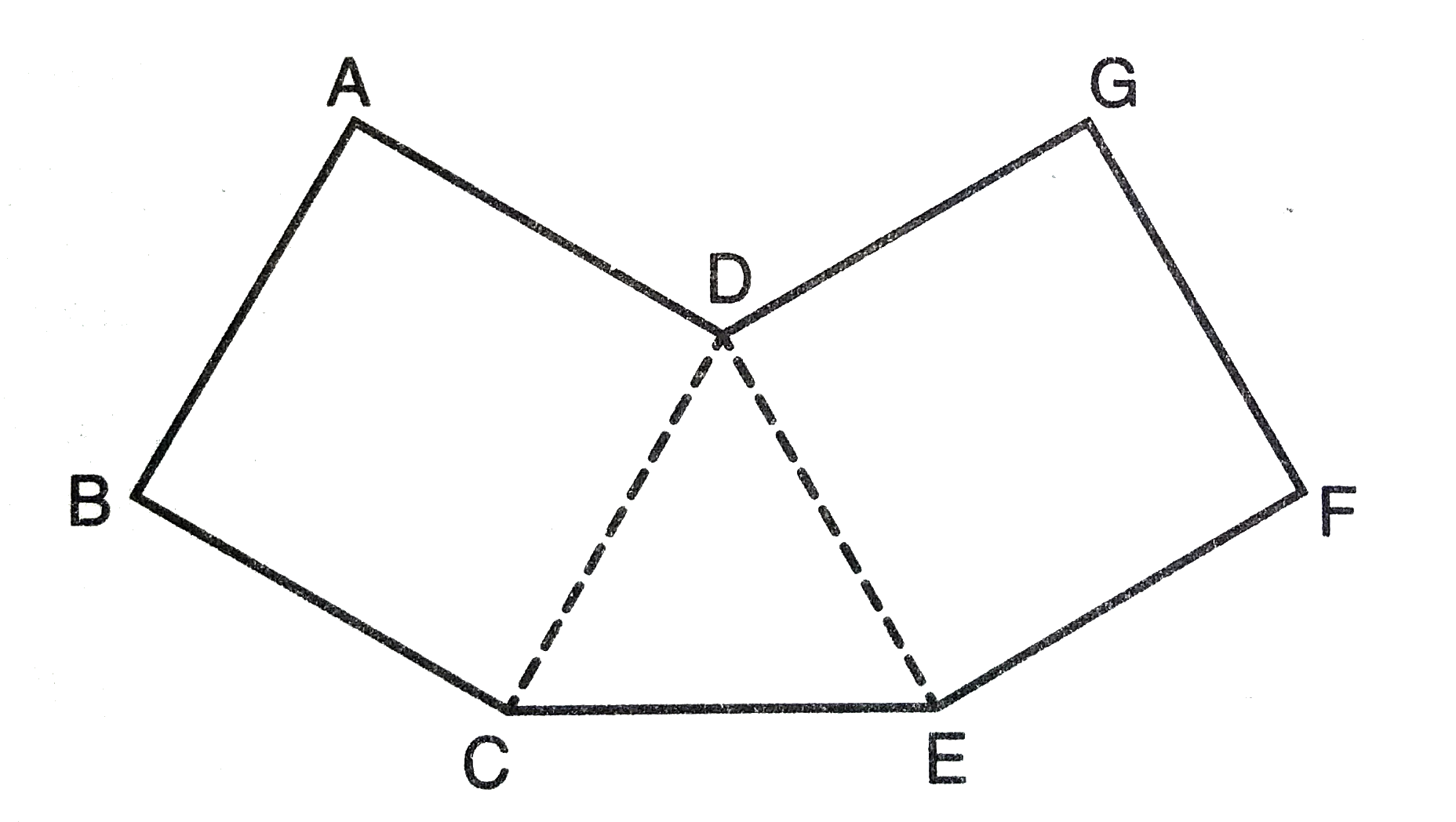
A sterling silver pendant is being designed to have the shape of polygon ABCDEFGD shown above where ABCD and EFGD are squares and triangle CDE is equilateral. If the area of △CDE is 27√3 square centimeter, what is the total linear distance around the pendant?
View SolutionFive square flower beds each of sides 1 m are dug on a piece of land 5 m long and 4 m wide. What is the area of the remaining part of the land?
View SolutionFour square flower beds, each of side 5m, are dug on a piece of land 10m long and 15m wide. What is the area of the remaining part of the land?
View SolutionOn a map, 1 inch represents 150 miles. What is the actual distance between two cities if they are 312 inches apart on the map ?
View SolutionBrian plans to complete a 100-mile bike race for charity. According to his registration materials, he will need to ride at an average speed of 12.5 miles per hour if he wants to complete the course before it closes. On a pratice ride the week before the race, Brain rides 60 miles and trackes his speed. For the first 30 miles, his average speed is 16 miles per hour, and for the next 30 miles, his average speed is 15 miles per hour. If Brian can match these speeds for the first 60 miles of the charity race, then he rests for that total of 1 hour after that, what approximately speed must he maintain for the last 40 miles in order to complete the ride on time?
View Solution

