A particle starts with uniform acceleration. Draw a graph taking the displacement(s) of the particle along y-axis and time(t) along x-axis. What is the curve known as?
Video Solution
Text Solution
While drawing the graph between any two quantities, the first step will be to establish a relation between them, in terms of known constants. Thus, for a uniformly accelerated motion, the relation between (s) and (t) is s=ut+12at2.
But since u=0,
∴ s=12at2
s is taken along y-axis, replace s by y and t being along x-axis , replace t by x.

Therefore, y=ax22 or x2=2ya which is of the form x2=4ay.
Therefore, the graph will be parabola with its axis as y i. e., (s) axis.
Notice that the portion of graph to the left of the displacement axis (i.e., towards negative time ) is omitted, as our point of interest lies in only the time elapsed after the beginning of motion.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A graph is drawn with a force along y-axis and time along x-axis. The area under the graph represent–
AMomentumBCoupleCMoment of the forceDImpulse of the forceFigure (i) and (i) show the displacement-time graphs of two particles moving along the x-axis. We can say that
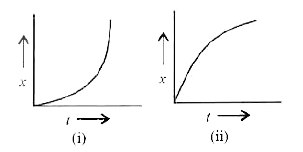 Aboth the particles are having a uniformly retarded motionBboth the particles are having a uniformly acceleraled motionCParticle (1) is having a uniformly accelerated motion while particle (i) is having a uniformly retarded motionDParticle (i) is having a uniformly retarded motion while particle (ii) is having a uniformly accelerated motion
Aboth the particles are having a uniformly retarded motionBboth the particles are having a uniformly acceleraled motionCParticle (1) is having a uniformly accelerated motion while particle (i) is having a uniformly retarded motionDParticle (i) is having a uniformly retarded motion while particle (ii) is having a uniformly accelerated motionA graph is plotted taking .∘C along the Y-axis and .∘F along the X-axis. It is a/an
AparabolaBstraight lineCellipseDcircle
A particle starts with some initial velocity with an acceleration along the direction of motion. Draw a graph depicting the variation of velocity (v) along y-axis with the variation of displacement(s) along x-axis.
View SolutionIf a graph is plotted by taking spectral emissive power along y-axis and wavelength along X-axis then the area below the graph above wavelength axis is
View SolutionFor a particle moving along x-axis, velocity-time graph is as shown in figure. Find the displacement of the particle?
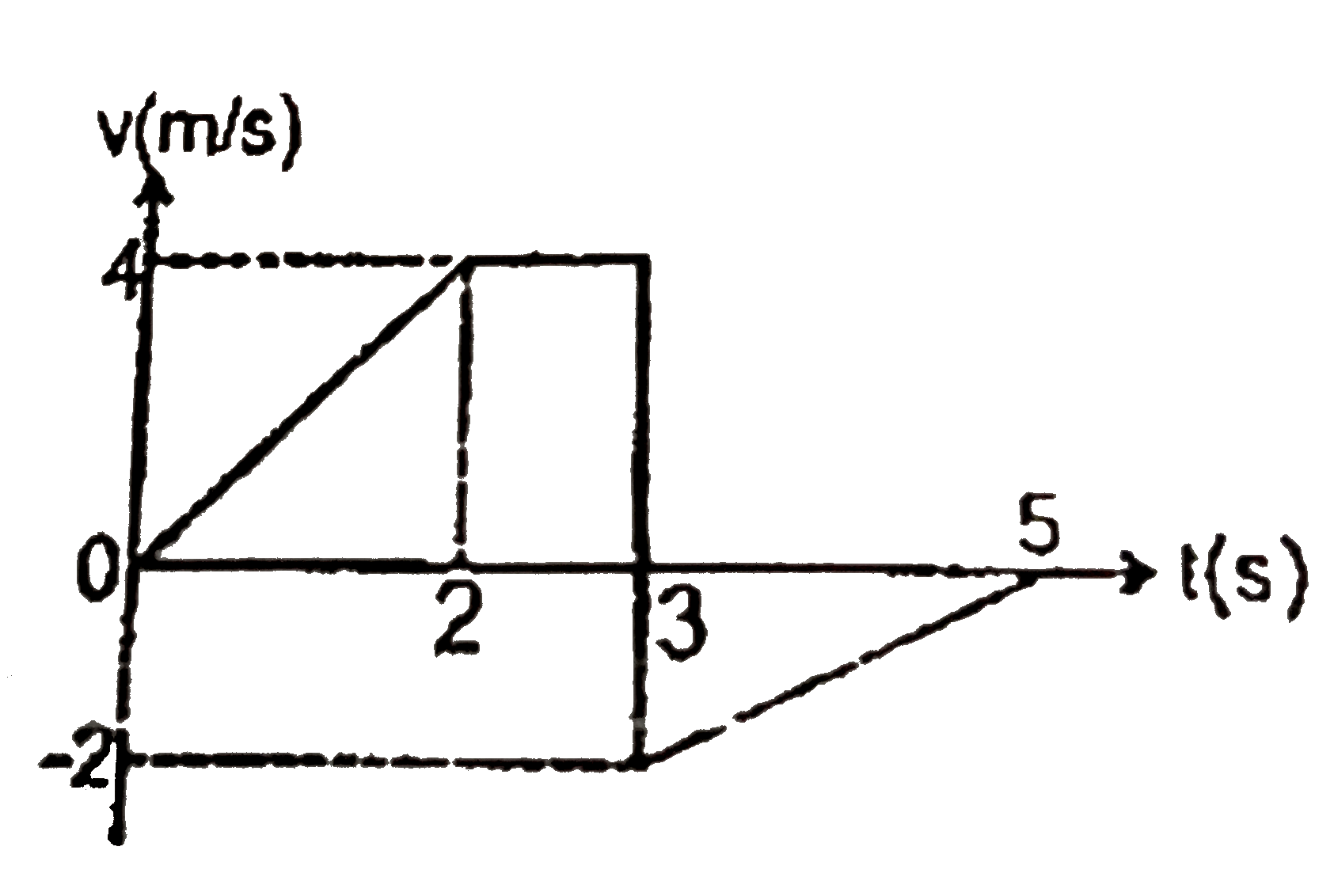
View SolutionIf the time-displacement graph of a particle is parallel to the-axis, the velocity of the particle is
View SolutionIf a cooling curve is drawn taking t(s) along X−axis and temperature (θ) along Y−axis, it appers as
View Solution



