A hot air balloon rising straight up from a level field is tracked by a range finder 500 ft from the lift-off point. At the moment the range finder's elevation angle is π4. The angle is increasing at the rate of 0.14 rad/min. How fast is the balloon rising at the moment ?

y=500tanθ
⇒ dydt=500dtanθdt=500dtanθdθdθdt
=500sec2θdθdt
=500×2×0.14
=140ft/min
Topper's Solved these Questions
Similar Questions
A hot air balloon rising straight up from a level field is tracked by a range finder 500 ft from the lift-off point. At the moment the range finder's elevation angle is π4, the angle is increasing at the rate of 0.14 rad/min. How fast is the balloon rising at that moment.
View SolutionA balloon and a bicycle. A balloon is rising vertically above a level, straight road at a constant rate of 1 ft/sec. Just when the balloon is 65 ft above the ground , a bicycle moving at a constant rate of 17 ft/sec passes under it . How fast is the distance between the bicycle and balloon increasing 3 sec later ?

View Solution
Knowledge Check
A hot air balloon is ascending straight up at a constant speed of 7.0 m/s. When the balloon is 12.0 m above the ground, a gun fires a pellet straight up from ground level with an initial speed of 30.0 m/s. Along the paths of the balloon and the same altitude at the same time. How far above ground level are these places ?
A1.5m/s2B4.5m/s2C3.0m/s2D6.0m/s2A balloon leaves from a point P rises at a uniform speed. After 6 minutes, an observer situated at a distance of 450√3 metres from point P observes that angle of elevation of the balloon is 60∘ Assume that point of observation and point P are on the same level. What is the speed (in m/s) of the balloon?
A4.25B3.75C4.5D3.45Rishu is riding in a hot air balloon. After reaching a point P, he spots a car parked at Bon the ground at an angle of depression of 30∘. The balloon rises further by 50 metres and now he spots the same car at an angle of depression of 45∘ and a lorry parked at B' at an angle of depression of 30∘. (Use √3 = 1.73)
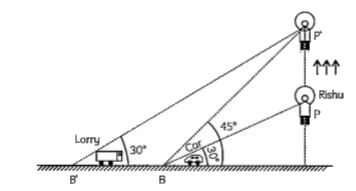
The measurement of Rishu facing vertically is the height. Distance is defined as the measurement of car/lorry from a point in a horizontal direction. If an imaginary line is drawn from the observation point to the top edge of the car/lorry, a triangle is formed by the vertical, horizontal and imaginary line.
The height of the balloon at point P' and distance AB are related as:Ah=x+50Bx=h+50Ch=50-xDx=50h
A balloon is rising vertically from a level field , suppose an on-looker sees it rising at 0.14 rad/min. when θ=π4 (when the on -looker is 500 m away from the launch spot ), how fast is balloon rising ?
View SolutionA balloon leaves from a point P rises at a uniform speed. After 6 minutes, an observer situated at a distance of 450√3 metres from point P observes that angle of elevation of the balloon is 60∘.Assume that point of observation and point P are on the same level. What is the speed (in m/s) of the balloon?
एक मुब्बारा एक समान गति से बिन्दु P से छोड़ा जाता है। 6 मिनट पश्चात, बिन्दु P से 450√3 मीटर दूरी पर एक समीक्षक है जो देखता है कि गुब्बारे का उन्नयन कोण 60∘ है। मान लीजिए कि समीक्षा बिन्दु तथा बिन्दु P एक ही स्तर पर है। गुब्बारे की गति [मी/ से.में] क्या है?
View SolutionRishu is riding in a hot air balloon. After reaching a point P, he spots a car parked at Bon the ground at an angle of depression of 30∘. The balloon rises further by 50 metres and now he spots the same car at an angle of depression of 45∘ and a lorry parked at B' at an angle of depression of 30∘. (Use √3 = 1.73)
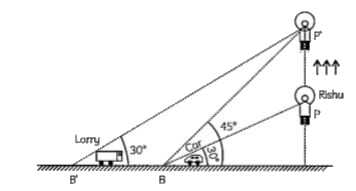
The measurement of Rishu facing vertically is the height. Distance is defined as the measurement of car/lorry from a point in a horizontal direction. If an imaginary line is drawn from the observation point to the top edge of the car/lorry, a triangle is formed by the vertical, horizontal and imaginary line.
The height of the balloon at point P, then
View SolutionRishu is riding in a hot air balloon. After reaching a point P, he spots a car parked at Bon the ground at an angle of depression of 30∘. The balloon rises further by 50 metres and now he spots the same car at an angle of depression of 45o and a lorry parked at B' at an angle of depression of 30∘. (Use √3 = 1.73)
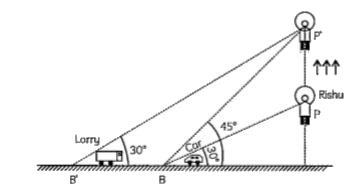
The measurement of Rishu facing vertically is the height. Distance is defined as the measurement of car/lorry from a point in a horizontal direction. If an imaginary line is drawn from the observation point to the top edge of the car/lorry, a triangle is formed by the vertical, horizontal and imaginary line.
If the height of the balloon at point P is 'h' m and distance AB is 'x' m, then 'x' and 'h' are related as:
View SolutionMr. Naik is a paramilitary Intelligence Corps officer who is tasked with planning a coup on the enemy at a certain date. Currently he is inspecting the area standing on top of the cliff. Agent Vinod is on a hot air balloon in the sky. When Mr. Naik looks down below the cliff towards the sea, he has Ajay and Maran in boats positioned to get a good vantage point.
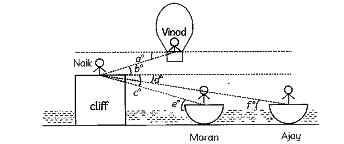
The main goal is to scope out the range and angles at which they should train their soldiers.
If the vertical height of the balloon from the top of the cliff is 12 m and ∠b=30∘, then the distance between the Naik and vinod is
View Solution

