Assertion : A uniform disc of radius R is performing impure rolling motion on a rough horizontal plane as shown in figur. After some time the disc comes to rest. It is possible only when v0=ω0R2

Reason : For a body performing pure rolling motion, the angular momentum uis conserved about any point in space.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is fasle
If Assertion is false but Reason is true
The correct Answer is:C
Angular momentum about bottommost point will be
L=mv0R−12mR2ω0
If L=0orv0=ω0R2, disc will come to rest after some time.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(A) Chapter Exercises
Explore 83 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Integer type q.
Explore 15 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
A disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View Solution
Knowledge Check
An object of mass M and radius R is performing pure rolling motion on a smooth horizontal surface under the action of a constant force F as shown in Fig. The object may be
 AdiskBringCsolid cylinderDhollow sphere
AdiskBringCsolid cylinderDhollow sphereΔ some in tan , a disk of radius 1.0 m is performing rolling on a rough horizontal surface. The velocity of point C in this shown direction is 5m/sec :
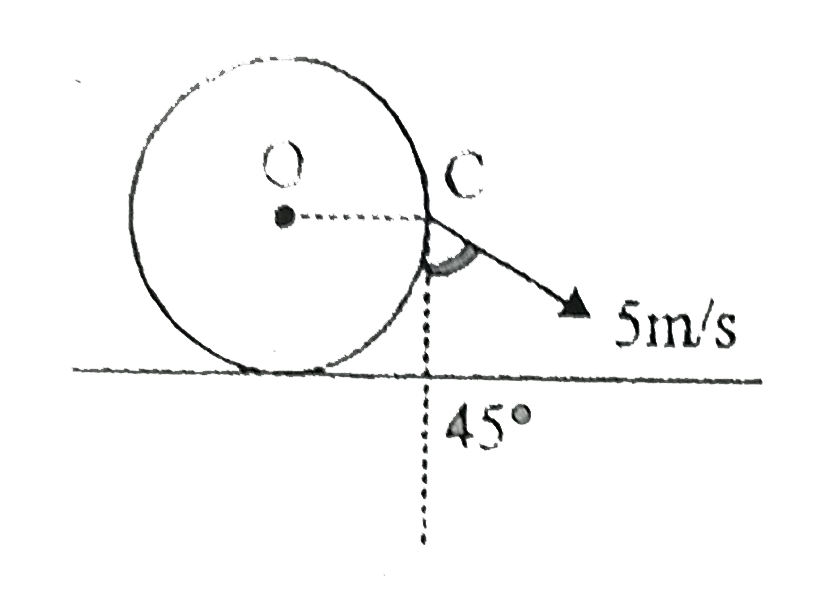 AInstantaneous centre is at a distance 1.0 m below centre OBInstantaneous centre is at a distance 0.05m below centre OCAngular velocity of disc is (5/√2) rad/secDVelocity of centre of mass is (5/√2) m/s
AInstantaneous centre is at a distance 1.0 m below centre OBInstantaneous centre is at a distance 0.05m below centre OCAngular velocity of disc is (5/√2) rad/secDVelocity of centre of mass is (5/√2) m/sA uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
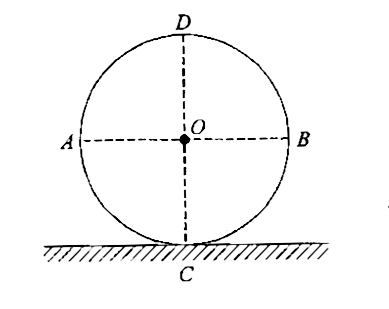 AmV202−mV20πBmv202+mv20πCmv202Dmv20
AmV202−mV20πBmv202+mv20πCmv202Dmv20
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

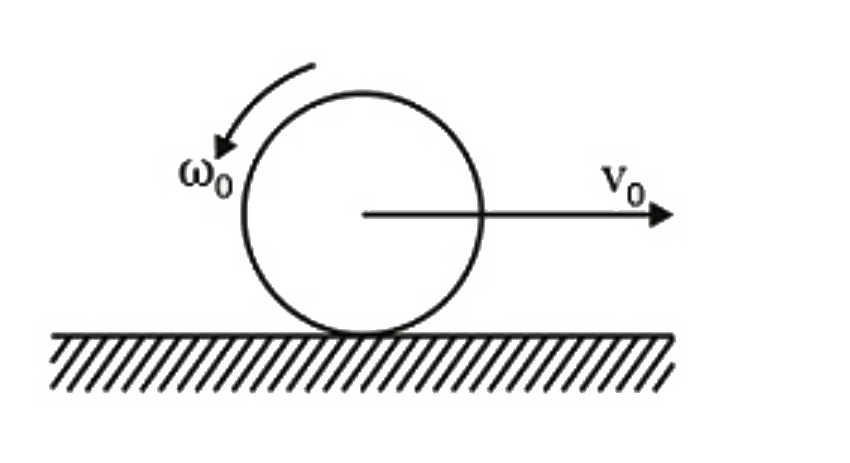
View SolutionA uniform circular disc of radius r placed on a rough horizontal plane has initial velocity v0 and angular ω0 as shown. The disc comes to rest after moving some distance in the direction of motion. Then
View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View SolutionA disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
View SolutionA uniform circular disc of radius r . 1placed on a rough horizontal plane has initial velocity v0 and an angular velocity ω0 as shown. The disc comes to rest after moving some distance in the direction of motion. Then
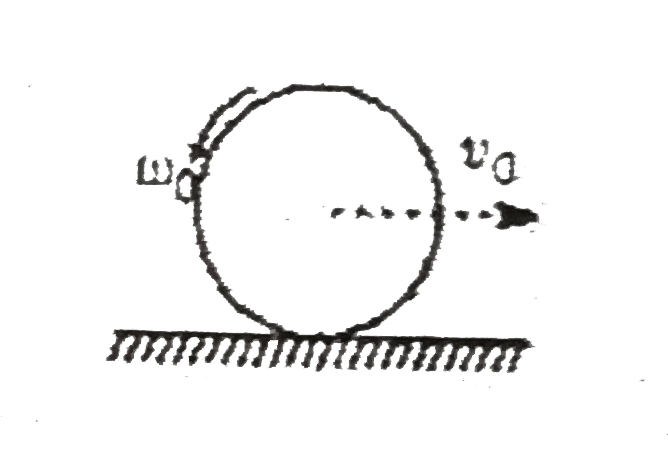
View Solution

