Assertion : Moment of inertia about an axis passing throught centre of mass is always minimum
Reason : Theorem of parallel axis can be applied for 2-D as well as 3-D bodies.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is fasle
If Assertion is false but Reason is true
The correct Answer is:C
When compared with many parallel axes, ICM is least. But it is wrong to say that parallel axis theorem can be applied to 2D body only.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(A) Chapter Exercises
Explore 83 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Integer type q.
Explore 15 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
Knowledge Check
The parallel axis theorem can be applied to
Aany two parallel axesBany two parallel-axes of which one must lie within the bodyCany two parallel-axes of which one must pass through the centre of mass of the body.Dany two parallel axes lying in the plane of the bodyAssertion: Moment of inertia of a rigid body about any axis passing through its centre of mass is minimum
Reason: From theorem of parallel axis
I=Icm+Mr2AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf assertion is true, but the reaction is false.DIf assertion is false but the reason is true.If I0 is the moment of inertia body about an axis passing through its center of mass. The moment about a parallel axis and at distance d is I=I0+Md2. The variation of I with d is
A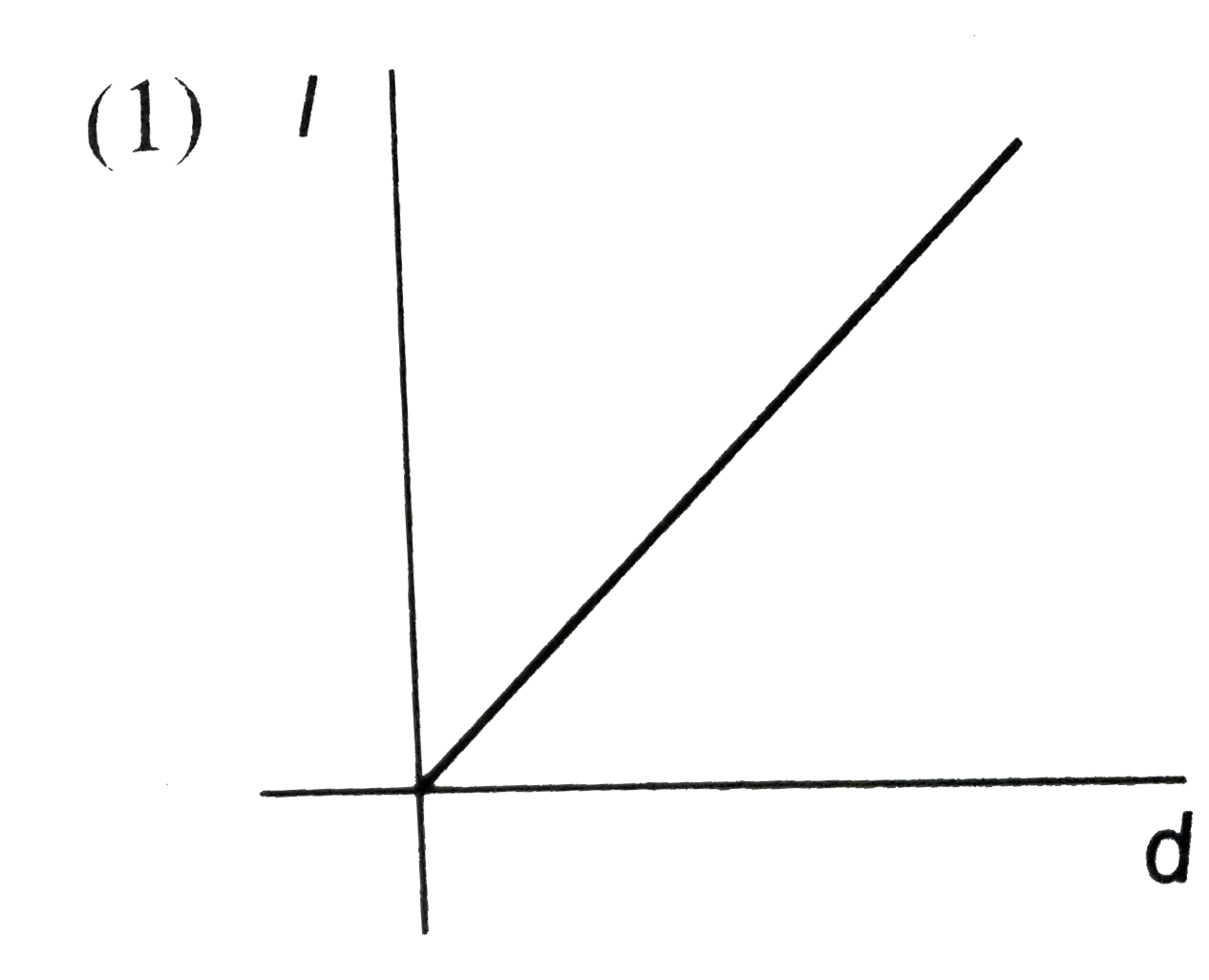 B
B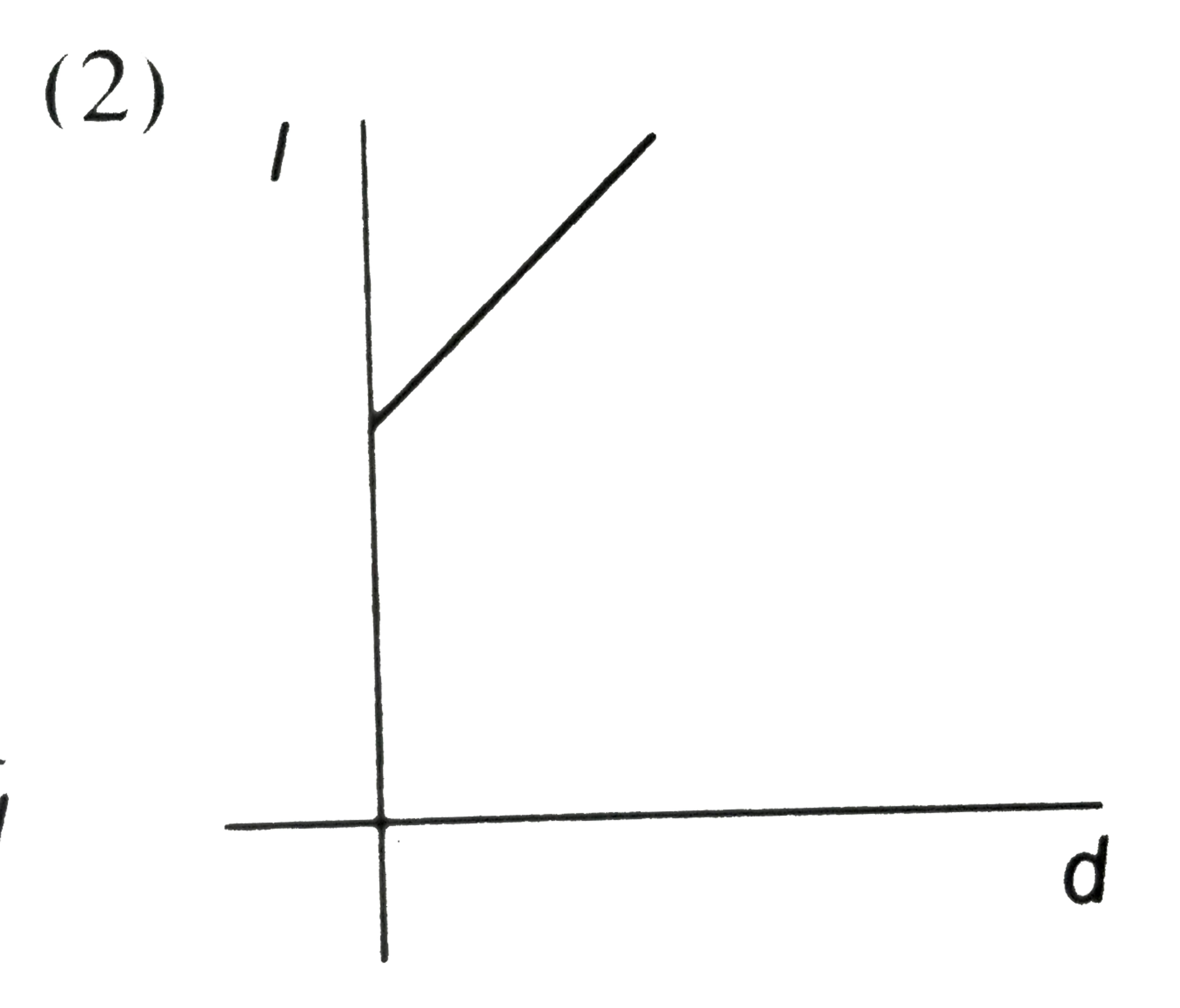 C
C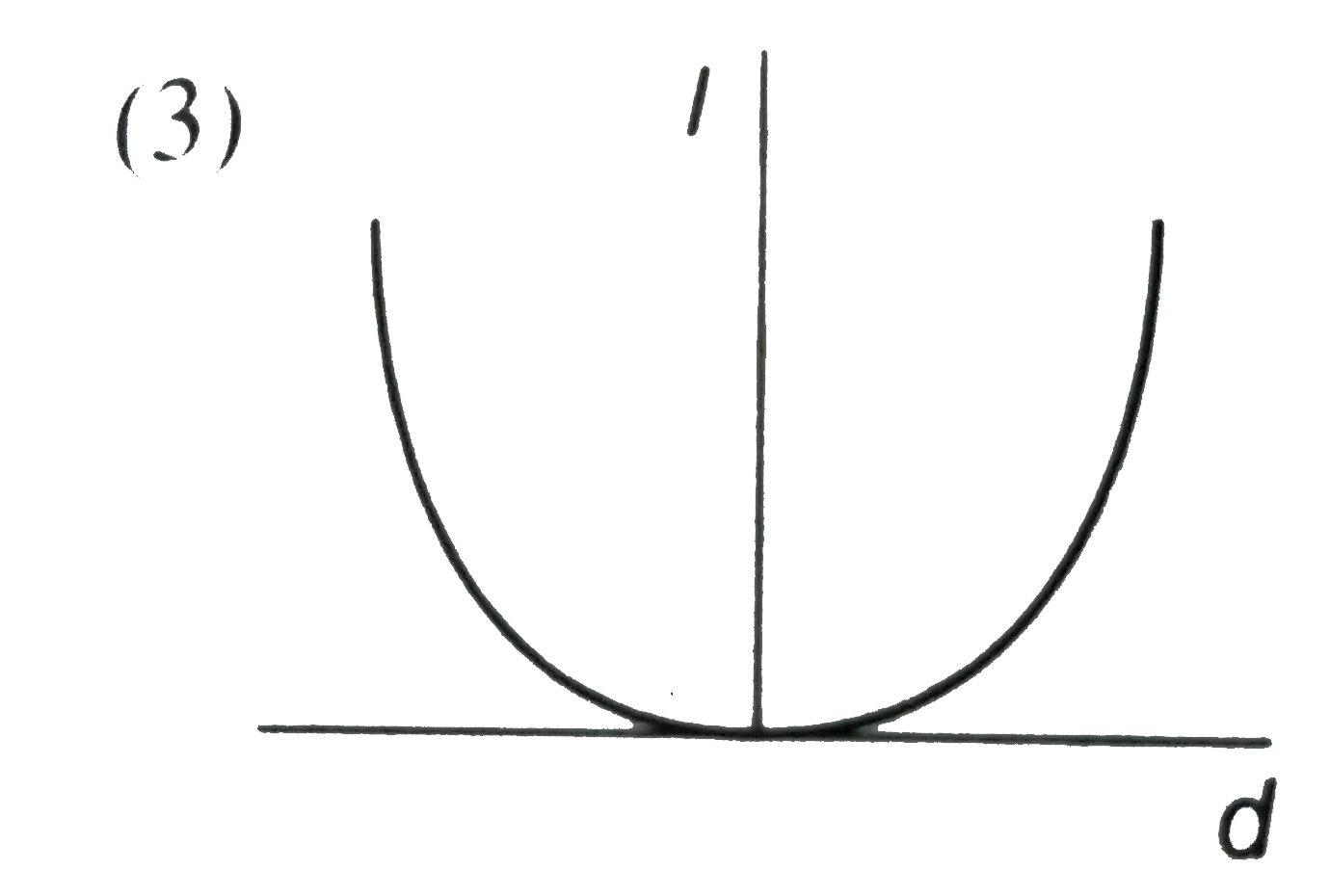 D
D
A solid sphere of mass M, radius R and having moment of inertia about an axis passing through the centre of mass as J, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains J. Then, radius of the disc will be
View SolutionA solid sphere of mass M and radius R having moment of inertia about an axis passing through the centre of mass as I, is recast into a disc of thickness I, whose moment of inertia about an axis passing through its edge and perpendicular to its plane remains I. Then, radius of the disc will be
View SolutionA solid sphere of mass M, radius R and having moment of inertia about as axis passing through the centre of mass as I, is recast into a disc of thickness t, whose moment of inertia about an axis passing through its edge and perpendicular to its plance remains I. Then, radius of the disc will be.
View SolutionA cylinder of 500 g and radius 10 cm has moment of inertia about an axis passing through its centre and parallel to its length is
View SolutionMoment of inertia of a rigid body about an axis passing through its centre of mass is I0 and moment of inertia of the same body about another axis parallel to the first axis is I. Then
View Solution


