While determining the refractive index of a liquid experimentally, the microscope was focussed at the bottom of a beaker, when its reading was 3.965 cm. on pouring liquid upto a height 2.537 cm inside the beaker, the reading of the refocussed microscope was 3.348 cm. Find the refractive index of the liquid.
The correct Answer is:1.321
To find the refractive index of the liquid, we can follow these steps:
Step 1: Identify the initial and final readings
- The initial reading of the microscope when focused at the bottom of the beaker is h1=3.965cm.
- After pouring the liquid up to a height of h=2.537cm, the new reading of the microscope is h2=3.348cm.
Step 2: Calculate the change in height
- The change in height (Δh) due to the liquid is given by:
Δh=h1−h2=3.965cm−3.348cm
- Performing the calculation:
Δh=0.617cm
Step 3: Relate the change in height to the refractive index
- The relationship between the height change and the refractive index (μ) is given by:
Δh=T(1−1μ)
where T is the height of the liquid column, which is T=2.537cm.
Step 4: Substitute the known values into the equation
- Rearranging the equation gives:
1μ=1−ΔhT
- Substituting Δh=0.617cm and T=2.537cm:
1μ=1−0.6172.537
Step 5: Calculate 0.6172.537
- Performing the division:
0.6172.537≈0.243
- Therefore:
1μ=1−0.243=0.757
Step 6: Calculate the refractive index μ
- Taking the reciprocal gives:
μ=10.757≈1.321
Final Answer
- The refractive index of the liquid is approximately μ≈1.321.
---
- The initial reading of the microscope when focused at the bottom of the beaker is h1=3.965cm.
- After pouring the liquid up to a height of h=2.537cm, the new reading of the microscope is h2=3.348cm.
- The change in height (Δh) due to the liquid is given by:
Δh=h1−h2=3.965cm−3.348cm
- Performing the calculation:
Δh=0.617cm
- The relationship between the height change and the refractive index (μ) is given by:
Δh=T(1−1μ)
where T is the height of the liquid column, which is T=2.537cm.
- Rearranging the equation gives:
1μ=1−ΔhT
- Substituting Δh=0.617cm and T=2.537cm:
1μ=1−0.6172.537
- Performing the division:
0.6172.537≈0.243
- Therefore:
1μ=1−0.243=0.757
- Taking the reciprocal gives:
μ=10.757≈1.321
- The refractive index of the liquid is approximately μ≈1.321.
Topper's Solved these Questions
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE F
Explore 10 Videos
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE I
Explore 12 Videos
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE A
Explore 15 Videos
- OPTICAL INSTRUMENTSBook:SL ARORAChapter:OPTICAL INSTRUMENTSExercise:Problems for self practice
Explore 35 Videos
- SOLIDS AND SEMICONDUCTOR DEVICESBook:SL ARORAChapter:SOLIDS AND SEMICONDUCTOR DEVICESExercise:PROBLEM_TYPE
Explore 9 Videos
Similar Questions
To determine the refractive index of a liquid experimentally, a mark is made on the beaker and a microscope was focussed on it, giving a reading of 3.42 cm. On pouring liquid till a height 2.68 cm inside the beaker, the reading of refocussed microscope is 3.38 cm. Calculate the refractive index of the liquid.
View SolutionFind the apparent depth of an object O placed at the bottom of a beaker as shown in which two layers of transparent liquids are filled

[22.67 cm]
View Solution
Knowledge Check
A microscope is focused on a coin lying at the bottom of a beaker. The microscope is now raised up by 1cm. To what depth should the water be poured into the beaker so that coin is again in focus ? (Refractive index of water is 4/3)
A1cmB4/3cmC3cmD4cmA travelling microscope is focussed on to a scratch on the bottom of a beaker. Water of refractive index 43 is poured in it. Then the microscope is to be lifted through 2 cm focus it again. Find the depth of water in the beaker.
A4 cmB8 cmC87cmD83cmAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
 A5/2B√(5/2)C√(3/2)D3/2
A5/2B√(5/2)C√(3/2)D3/2
A jar 15cm long is filled with a transparent liquid. When viewed from the top, its bottom appears to be 12cm below. What is the refractive index of the liquid ?
View SolutionIn Fig. a plane mirror lies at a height h above the bottom of a beaker containingwater (refractive index μ) upto a height f. Find the position of the image of the
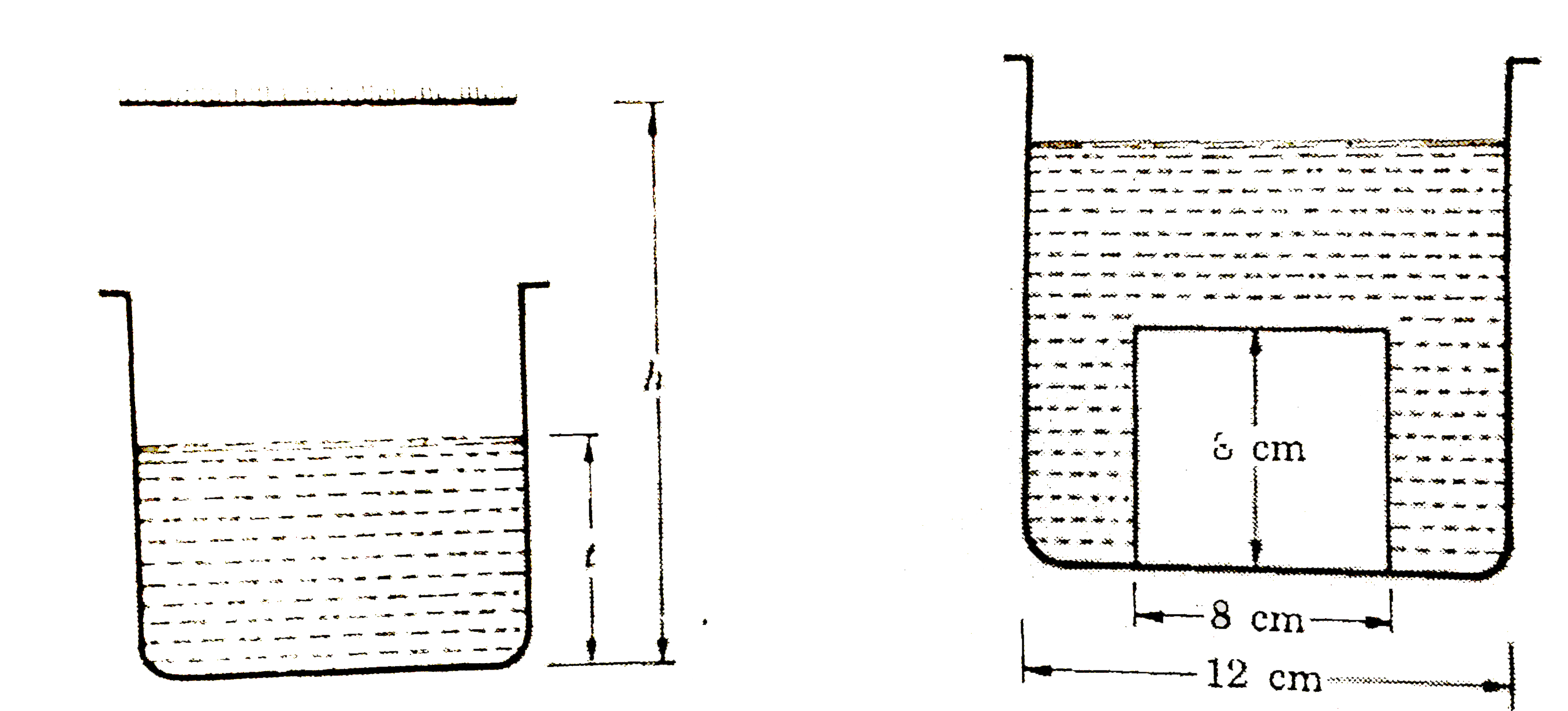
View SolutionA convex lens is held 45cm above the bottom of an empty tank. The image of a point at the bottom of a tank is formed 36cm above the lens. Now, a liquid is poured into the tank to a depth of 40cm. It is found that the distance of the image of the same point on the bottom of the tank is 48cm above the lens. Find the refractive index of the liquid.
View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The beaker height is 3h and its radius h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is

View SolutionAn observer can see through a pin-hole the top end of a thin rod of height h, placed as shown in the figure. The height of beaker is 3h and its radius is h. When the beaker is filled with a liquid up to a height 2h, he can see the lower end of the rod. Then the refractive index of the liquid is
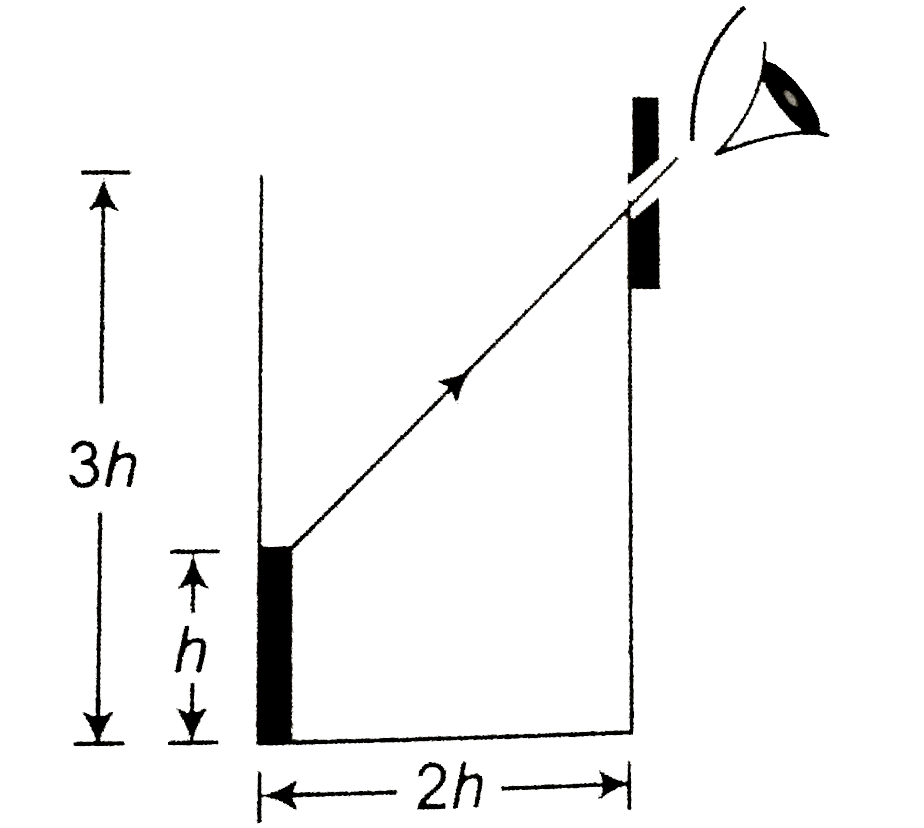
View Solution

