Calculate the index of refraction of a liquid from the following into glass:
(a) Reading for the bottom of an empty beaker: 11.324 cm
(b) Reading for the bottom of the beaker, when partially filled with the liquid: 11.802 cm
(c) Reading for the upper level of the liquid in the beaker: 12.895cm
The correct Answer is:1.437
Step by step video, text & image solution for Calculate the index of refraction of a liquid from the following into glass: (a) Reading for the bottom of an empty beaker: 11.324 cm (b) Reading for the bottom of the beaker, when partially filled with the liquid: 11.802 cm (c) Reading for the upper level of the liquid in the beaker: 12.895cm by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE F
Explore 10 Videos
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE I
Explore 12 Videos
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE A
Explore 15 Videos
- OPTICAL INSTRUMENTSBook:SL ARORAChapter:OPTICAL INSTRUMENTSExercise:Problems for self practice
Explore 35 Videos
- SOLIDS AND SEMICONDUCTOR DEVICESBook:SL ARORAChapter:SOLIDS AND SEMICONDUCTOR DEVICESExercise:PROBLEM_TYPE
Explore 9 Videos
Similar Questions
The apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View SolutionWhen half of the total volume of an empty beaker of mass 100 g is filled with water, its mass is found to be 500 g and when the remaining volume of the beaker is filled with a liquid, its mass is found to be 1 kg. Calculate the density of the liquid.
View Solution
Knowledge Check
Calculate the index of refraction of a liquid from the following into glass:
(a) Reading for the bottom of an empty beaker: 11.324 cm
(b) Reading for the bottom of the beaker, when partially filled with the liquid: 11.802 cm
(c) Reading for the upper level of the liquid in the beaker: 12.895cmA1.232B1.389C1.28D1.437A small coin is resting on the bottom of a beaker filled with liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface. How fast is the light travelling in the liquid?
 A2.4×108ms−1B3.0×108ms−1C1.2×108ms−1D1.8×108ms−1
A2.4×108ms−1B3.0×108ms−1C1.2×108ms−1D1.8×108ms−1A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)
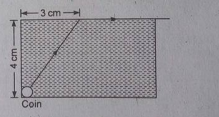
How fast is the light travelling in the liquid ?A1.8×108m/sB2.4×108m/sC3.0×108m/sD1.2×108m/s
While determining the refractive index of a liquid experimentally, the microscope was focussed at the bottom of a beaker, when its reading was 3.965 cm. on pouring liquid upto a height 2.537 cm inside the beaker, the reading of the refocussed microscope was 3.348 cm. Find the refractive index of the liquid.
View SolutionFind the apparent depth of an object O placed at the bottom of a beaker as shown in which two layers of transparent liquids are filled

[22.67 cm]
View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface (see figure)

How fast is the light travelling in the liquid ?
View SolutionA small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface How fast is the light travelling the liquid ?
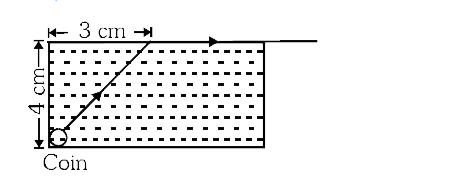
View Solution
A real image of an object is formed by a conex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index 1.4 to a depth of 7 cm. In order to get the image again at the bottom the beaker shoud be moved
View Solution

