
A real image of an object is formed by a conex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index 1.4 to a depth of 7 cm. In order to get the image again at the bottom the beaker shoud be moved
downward by 2 cm
upward by 2 cm
downward by 3 cm
upward by 3 cm
The correct Answer is:A
Shift by water tank
7(1−11.4)=2cm away from lens
Topper's Solved these Questions
- REFRACTION AT SPHERICAL SURFACESBook:CP SINGHChapter:REFRACTION AT SPHERICAL SURFACESExercise:EXERCISES
Explore 105 Videos
- REFLECTION OF LIGHTBook:CP SINGHChapter:REFLECTION OF LIGHTExercise:EXERCISES
Explore 67 Videos
- REFRACTION OF LIGHT BY PLANE SURFACESBook:CP SINGHChapter:REFRACTION OF LIGHT BY PLANE SURFACESExercise:Exercises
Explore 110 Videos
Similar Questions
An object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
View SolutionThe apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View Solution
Knowledge Check
A metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
A7.5cmB6.75cmC4.5cmD1.5cm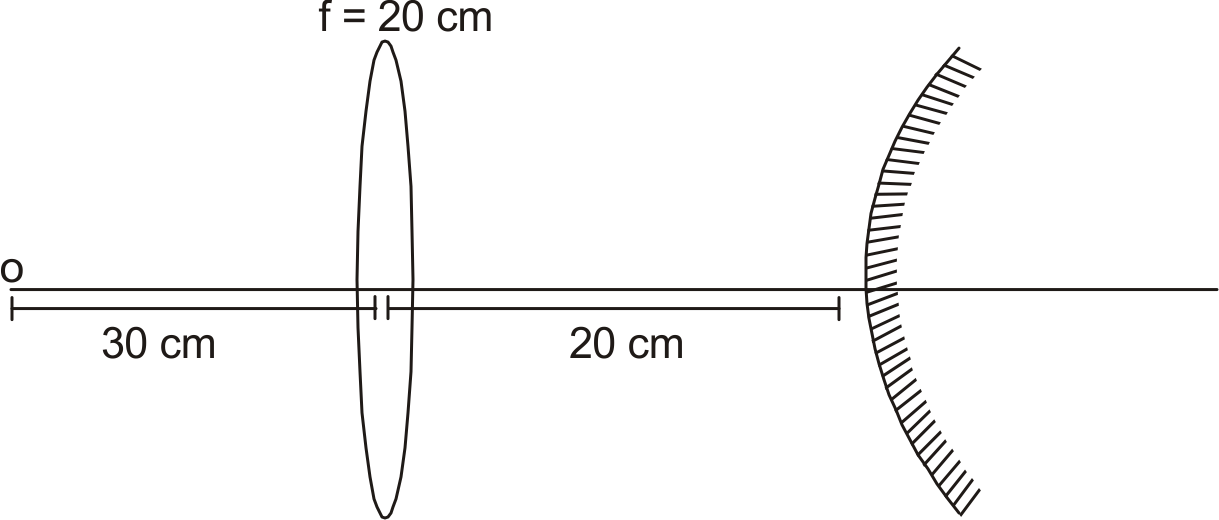
The lens shown is equiconvex having refractive Index. 1.5. In the situation shown the final image of object coincides with the object. The region between lens and mirror is now filled with a liquid of Rrefractive Index 2. Then find the separation between O & image formed by convex mirror.A33 cmB66 cmC16 cmD32 cmA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
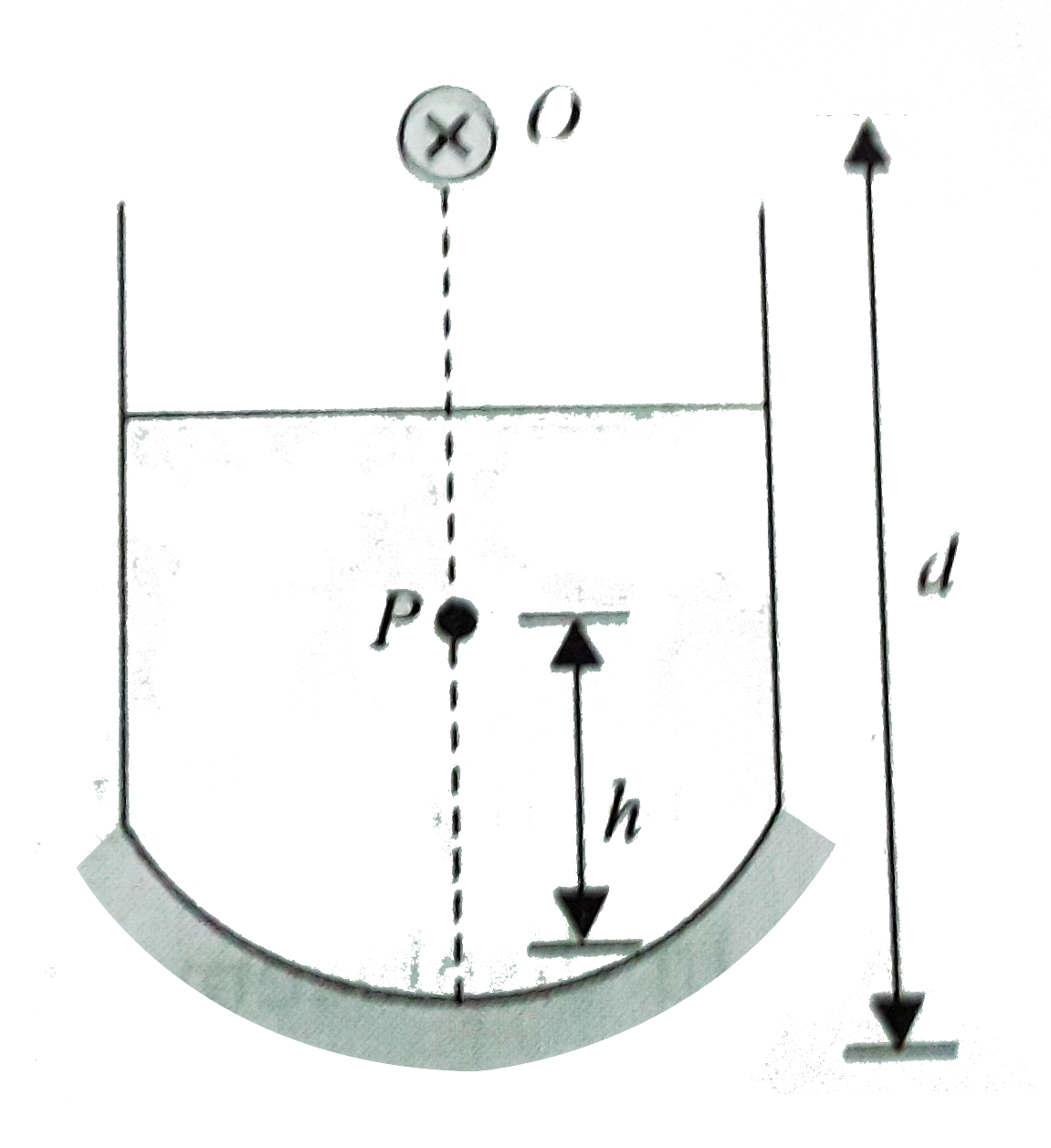 Ah(1−1μ)B2hμ−1CzeroD2hμ
Ah(1−1μ)B2hμ−1CzeroD2hμ
A convex lens is held 45cm above the bottom of an empty tank. The image of a point at the bottom of a tank is formed 36cm above the lens. Now, a liquid is poured into the tank to a depth of 40cm. It is found that the distance of the image of the same point on the bottom of the tank is 48cm above the lens. Find the refractive index of the liquid.
View SolutionA man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
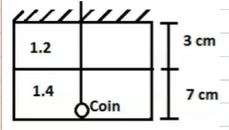
View SolutionA boy holds a convex lens 30 cm above the base of an empty vessel. The real image of the bottom of the vessel is formed 20 cm above the lens. The boy fills a liquid in the vessel up to a depth of 25 cm and finds that the real image of the bottom of the vessel is now 30 cm above the lens. Find the refractive index of the liquid.
View SolutionA glass beaker has diameter 4cm wide at the bottom. An observer observes the edge of bottom when beaker is empty as shown in figure. When the beaker is completely filled with liquid of refractive index n=√5/2, he can just see the centre of bottom, then the height of glass beaker is :

View SolutionA tank is filled with water to a height of 15.5cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 8.5cm. If water is replaced by a liquid of refractive index 1.94 up to the same height by what distance would the microscope have to be moved to focus on the needle again ?
View Solution

