An object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
To find the apparent depth of an object placed at the bottom of a tank filled with liquid, we can use the relationship between the real depth, apparent depth, and the refractive index of the liquid. Here’s how to solve the problem step by step:
Step 1: Understand the given information
- The actual (real) depth of the tank (h) = 10 cm
- The refractive index of the liquid (μ) = 1.6
Step 2: Use the formula for apparent depth
The relationship between the real depth (h), apparent depth (h'), and the refractive index (μ) is given by the formula:
μ=Real DepthApparent Depth
This can be rearranged to find the apparent depth:
Apparent Depth=Real Depthμ
Step 3: Substitute the values into the formula
Now, substitute the known values into the formula:
Apparent Depth=10cm1.6
Step 4: Calculate the apparent depth
Now, perform the division:
Apparent Depth=6.25cm
Conclusion
The apparent depth of the object is 6.25 cm.
---
- The actual (real) depth of the tank (h) = 10 cm
- The refractive index of the liquid (μ) = 1.6
The relationship between the real depth (h), apparent depth (h'), and the refractive index (μ) is given by the formula:
μ=Real DepthApparent Depth
This can be rearranged to find the apparent depth:
Apparent Depth=Real Depthμ
Now, substitute the known values into the formula:
Apparent Depth=10cm1.6
Now, perform the division:
Apparent Depth=6.25cm
The apparent depth of the object is 6.25 cm.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:PRACTICE PROBLEMS (1)
Explore 13 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:PRACTICE PROBLEMS (2)
Explore 9 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
The apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View SolutionA luminous object O is located at the bottom of a big pool of liquid of refractive index μ and depth h. The object O emits rays upwards in all directions, so that a circle of light is formed at the surface of the liquid by the rays which are refracted into the air. what happens to the rays beyond the circle ? Determine the radius and the area of the circle .
View Solution
Knowledge Check
A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
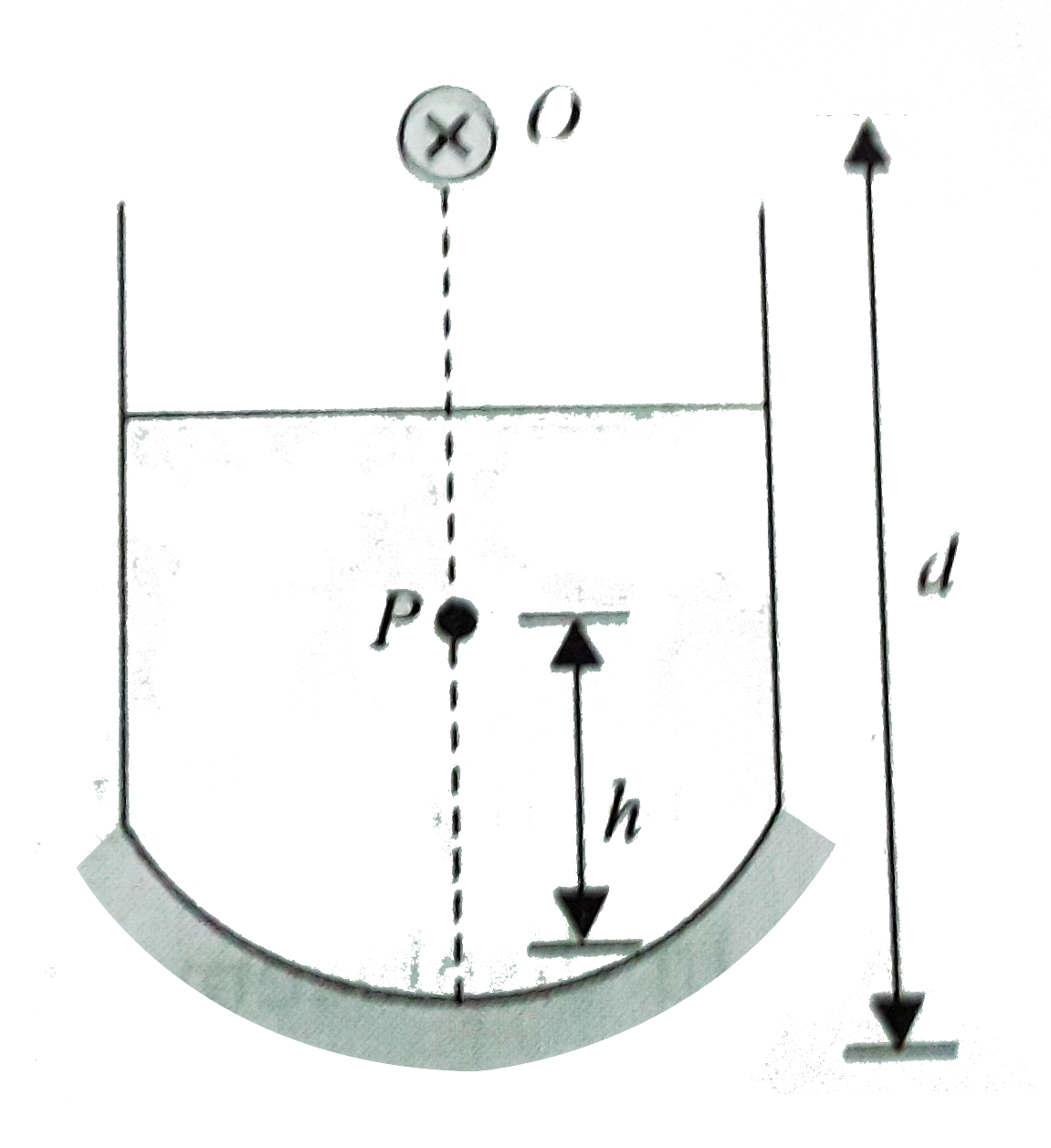 Ah(1−1μ)B2hμ−1CzeroD2hμ
Ah(1−1μ)B2hμ−1CzeroD2hμThe apparent depth of an object O from AB is
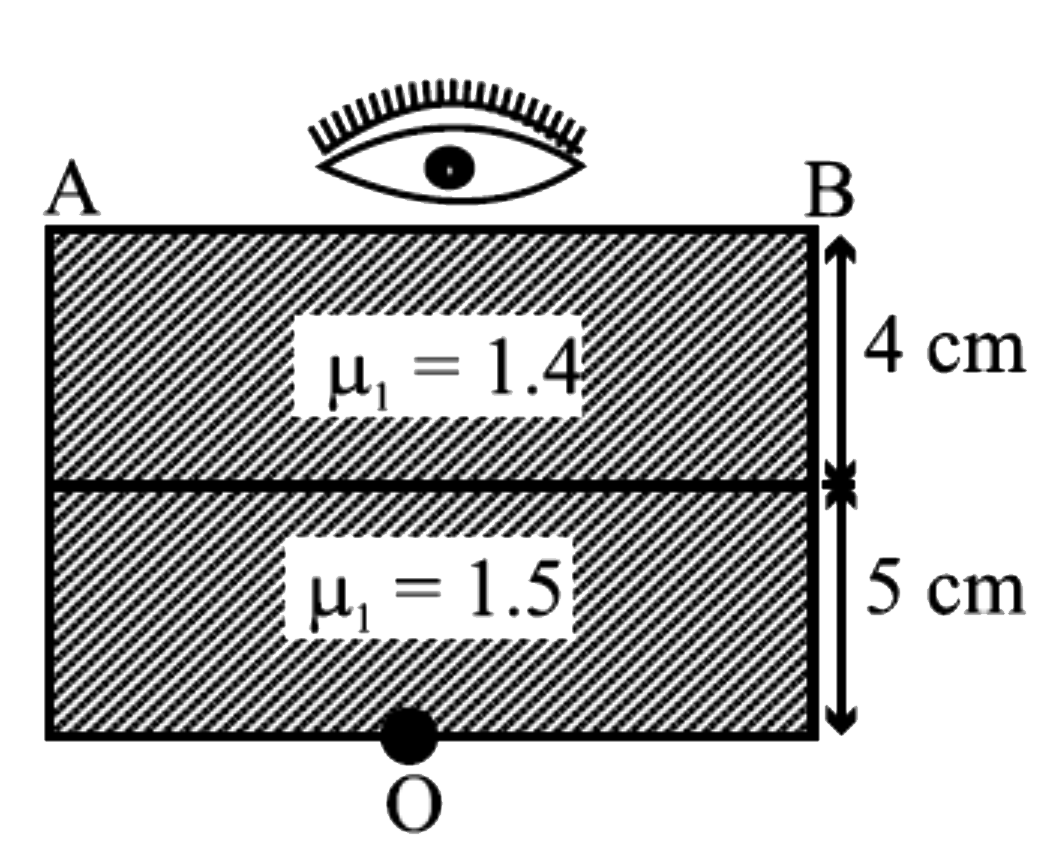 A4.29cmB5.43 cmC6.19 cmD5.99 cm
A4.29cmB5.43 cmC6.19 cmD5.99 cm
A real image of an object is formed by a conex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index 1.4 to a depth of 7 cm. In order to get the image again at the bottom the beaker shoud be movedAdownward by 2 cmBupward by 2 cmCdownward by 3 cmDupward by 3 cm
There is a plane mirror at the bottom of tank filled with water having refractive index 4/3. A point object is placed at a height 10 cm above the bottom. What will be the apparent distance between point object and its image in plane mirror as observed by an observer outside the liquid in air ? Line joining observer and object is normal to the surface of water.
View SolutionA vessel of depth d is half filled with a liquid of refractive index μ1 and the other half is filled with a liquid of refractive index μ2. The apparent depth of the vessel, when looked at normally, is
View SolutionA plane mirror is placed at the bottom of a tank containing a liquid of refractive index μ. P is a small object at a height h above the mirror. An observes P and its image in the mirror. The apparent distance between two will be
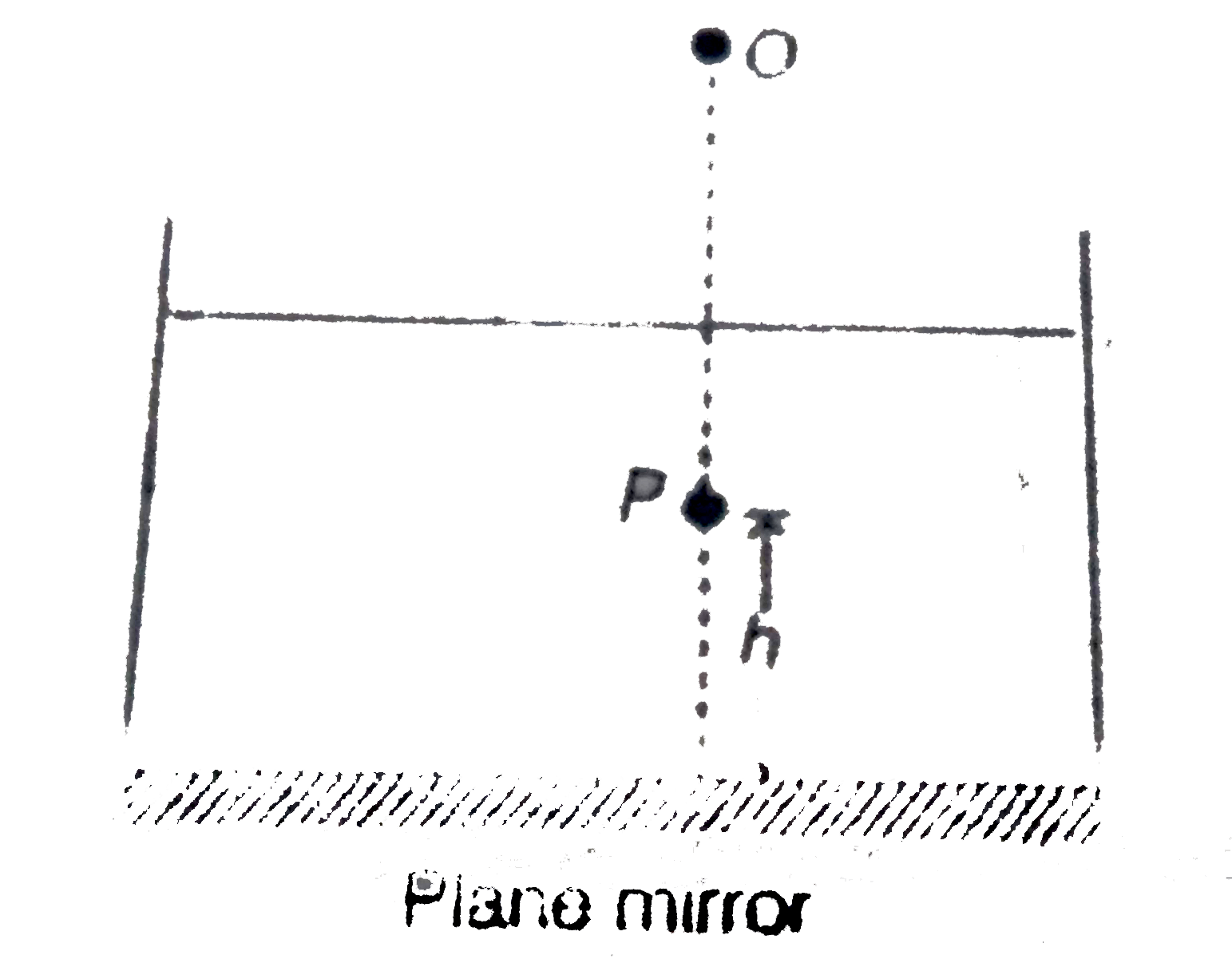
View SolutionA vessel of depth 2d cm is half filled with a liquid of refractive index μ1 and the upper half with a liquid of refractive index μ2. The apparent depth of the vessel seen perpendicularly is
View SolutionA vessel of depth 2d is half filled with a liquid of refractive index n1 and the upper half with a liquid of refractive index n2. The apparent depth of the vessel when seen normally from the top is
View Solution
