A glass sphere of radius 15 cm has a small bubble 6 cm from its centre. The bubble is viewed along a diameter of the sphere from the side on which it lies. How for from the surface will it appear to be if the refractive index of glass is 1.5 ?
The correct Answer is:Virtual image is seen at 7.5 cm from the spherical surface
To solve the problem step by step, we will use the concepts of optics, specifically the refraction of light through a spherical medium.
Step 1: Understand the Given Information
We have a glass sphere with:
- Radius (R) = 15 cm
- A small bubble located 6 cm from the center of the sphere.
Step 2: Determine the Object Distance (u)
The object distance (u) is measured from the center of the sphere to the bubble. Since the bubble is 6 cm from the center, we can find the distance from the surface of the sphere to the bubble:
- Distance from the center to the surface = Radius = 15 cm
- Therefore, the distance from the surface to the bubble (u) = 15 cm - 6 cm = 9 cm.
Since we are using the sign convention where distances measured in the direction of incident light are negative, we have:
- u = -9 cm.
Step 3: Identify the Refractive Indices
- Refractive index of air (μ1) = 1.0
- Refractive index of glass (μ2) = 1.5
Step 4: Apply the Refraction Formula
We will use the formula for refraction at a spherical surface:
μ1v−μ2u=μ1−μ2R
Substituting the known values:
1v−1.5−9=1−1.515
Step 5: Simplify the Equation
This simplifies to:
1v+1.59=−0.515
Calculating the right side:
−0.515=−130
Now, we have:
1v+1.59=−130
Step 6: Calculate 1.59
Calculating 1.59:
1.59=16
Step 7: Substitute and Solve for 1v
Now substituting back:
1v+16=−130
To solve for 1v, we need a common denominator. The common denominator for 6 and 30 is 30:
1v+530=−130
Subtracting 530 from both sides:
1v=−130−530=−630=−15
Step 8: Find v
Taking the reciprocal gives:
v=−5 cm
Step 9: Interpret the Result
The negative sign indicates that the image is virtual and located on the same side as the object (the bubble).
Step 10: Calculate the Distance from the Surface
Since the radius of the sphere is 15 cm, the distance of the virtual image from the surface of the sphere is:
Distance from surface=15cm−5cm=10cm.
Final Answer
The bubble will appear to be 10 cm from the surface of the glass sphere.
---
We have a glass sphere with:
- Radius (R) = 15 cm
- A small bubble located 6 cm from the center of the sphere.
The object distance (u) is measured from the center of the sphere to the bubble. Since the bubble is 6 cm from the center, we can find the distance from the surface of the sphere to the bubble:
- Distance from the center to the surface = Radius = 15 cm
- Therefore, the distance from the surface to the bubble (u) = 15 cm - 6 cm = 9 cm.
- u = -9 cm.
- Refractive index of air (μ1) = 1.0
- Refractive index of glass (μ2) = 1.5
We will use the formula for refraction at a spherical surface:
μ1v−μ2u=μ1−μ2R
1v−1.5−9=1−1.515
This simplifies to:
1v+1.59=−0.515
−0.515=−130
1v+1.59=−130
Calculating 1.59:
1.59=16
Now substituting back:
1v+16=−130
1v+530=−130
1v=−130−530=−630=−15
Taking the reciprocal gives:
v=−5 cm
The negative sign indicates that the image is virtual and located on the same side as the object (the bubble).
Since the radius of the sphere is 15 cm, the distance of the virtual image from the surface of the sphere is:
Distance from surface=15cm−5cm=10cm.
The bubble will appear to be 10 cm from the surface of the glass sphere.
Topper's Solved these Questions
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE F
Explore 10 Videos
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE I
Explore 12 Videos
- RAY OPTICSBook:SL ARORAChapter:RAY OPTICSExercise:TYPE A
Explore 15 Videos
- OPTICAL INSTRUMENTSBook:SL ARORAChapter:OPTICAL INSTRUMENTSExercise:Problems for self practice
Explore 35 Videos
- SOLIDS AND SEMICONDUCTOR DEVICESBook:SL ARORAChapter:SOLIDS AND SEMICONDUCTOR DEVICESExercise:PROBLEM_TYPE
Explore 9 Videos
Similar Questions
A glass sphere of radius 5 cm has a small bubble at a distance 2 cm from its centre. The bubble is viewed along a Diameter of the sphere from the side on which it lies.How far from the surface will it appear.Refractive index of glass is 1.5
2.5 cm behind the surface
View SolutionA spherical solid glass paper weight of diameter 6 cm has a small air bubble at a distance of 1.5 cm from the centre. If the air bubble be viewed from the side to which it is nearest along the line joining the bubble and the centre, find where will it appear.
View Solution
Knowledge Check
In a glass sphere, there is a small bubble 2×10−2m from its centre, if the bubble is viewed along a diameter of the sphere, from the side on which it lies, how far from the surface will it appear, the radius of glass sphere is 5×10−2m and refractive index of glass is 1.5?
A2.5×10−2mB3.2×10−2mC6.5×10−2mD0.2×10−2mA glass sphere (μ =1.5) of radius 20 cm has small air bubble 4 cm below its centre. The sphere is viewed from outside and along vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
A13.33B26.67C15D30A small object is enclosed in a sphere of solid glass 8cm in radius. It is situated 2cm from the centre and is viewed from the side of which it is nearer. Where will it appear to be if μ of glass =1.5/
A6cm from the centreB4cm from the nearer surfaceC315cm from the nearer surfaceD323cm from the centre
A glass cube of side 0.6 m contains a small air bubble. It appears to be at a distacne of 0.1 m when observed from the opposite face. Find the actual distance of the bubble from the first face and also the refractive index of glass.
View SolutionA glass sphere of (μ=1.5) with a radius of 15.0cm has a tiny air bubble 5cm above its centre. The sphere is viewed looking down along the extended radius containing the bubble. What is the apparent depth of the bubble below the surface of the sphere?
View SolutionIf the refractive index from air to glass is 1.5 ,and the refractive index of water is 1.33. What is the refractive index from glass into water?
View SolutionA small air bubble in a glass sphere of radius 2cm appears to be 1cm from the surface when looked at, along a diameter. If the refractive index of glass is 1.5, find the true position of the air bubble.
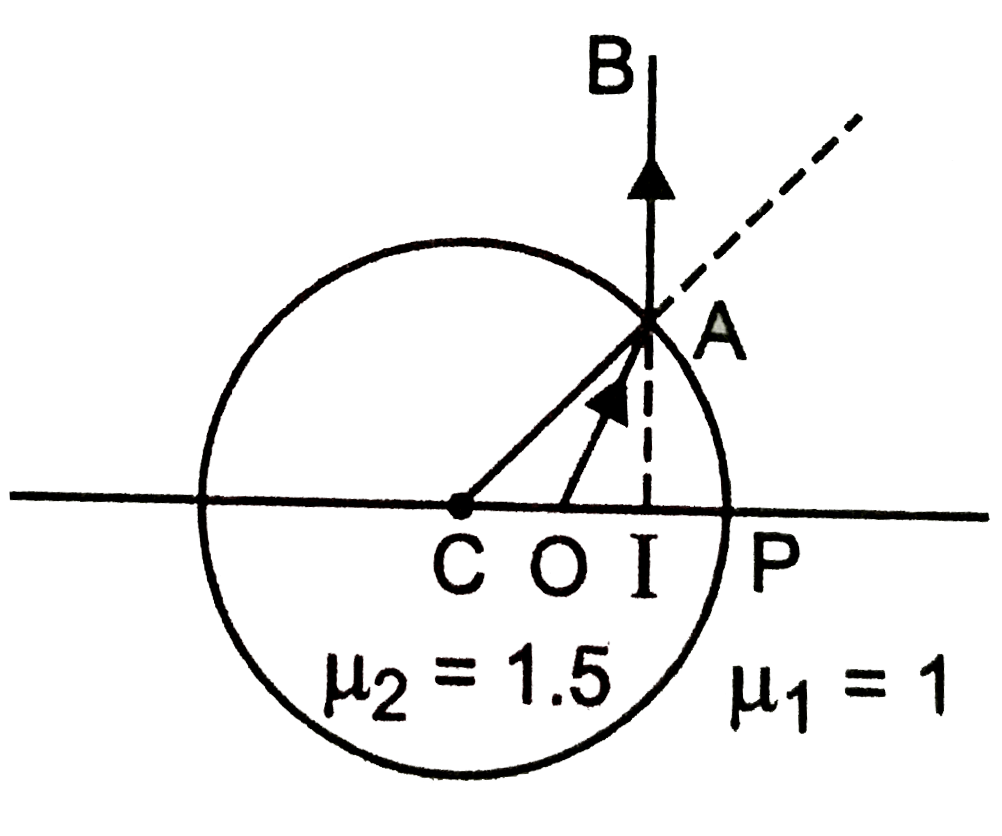 .
.
View SolutionA glass slab of thickness 12 cm is placed on a table. The level surface of the slab has a black spot. At what depth from the upper surface will the spot appear when viewed from above?
(Refractive index of glass = 1.5)
View Solution

