Passage IV) Angular frequency in SHM is given by ω=√km. Maximum acceleration in SHM is ω2 A and maximum value of friction between two bodies in contact is μN, where N is the normal reaction between the bodies.
Now the value of k, the force constant is increased, then the maximum amplitude calcualted in above question will
remain same
increase
decrease
data is insufficient
The correct Answer is:C
Step by step video, text & image solution for Passage IV) Angular frequency in SHM is given by omega=sqrt(k/m). Maximum acceleration in SHM is omega^(2) A and maximum value of friction between two bodies in contact is muN, where N is the normal reaction between the bodies. Now the value of k, the force constant is increased, then the maximum amplitude calcualted in above question will by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Matrix matching type questions
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Integer type questions
Explore 14 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:More than one option is correct
Explore 50 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
Statement - 1 : Maximum value of friction force between two surfaces is μ× normal reaction.
where μ = coefficient of friction between surfaces.
Statement - 2 : Friction force between surfaces of two bodies is always less than or equal to externally applied force.
View SolutionTwo particles are in SHM with the same amplitude and frequency along the same line and about the same point. If the maximum separation between them is √3 times their amplitude, the phase difference between them is 2πn. Find value of n
View Solution
Knowledge Check
Passage IV) Angular frequency in SHM is given by ω=√km. Maximum acceleration in SHM is ω2 A and maximum value of friction between two bodies in contact is μN, where N is the normal reaction between the bodies.
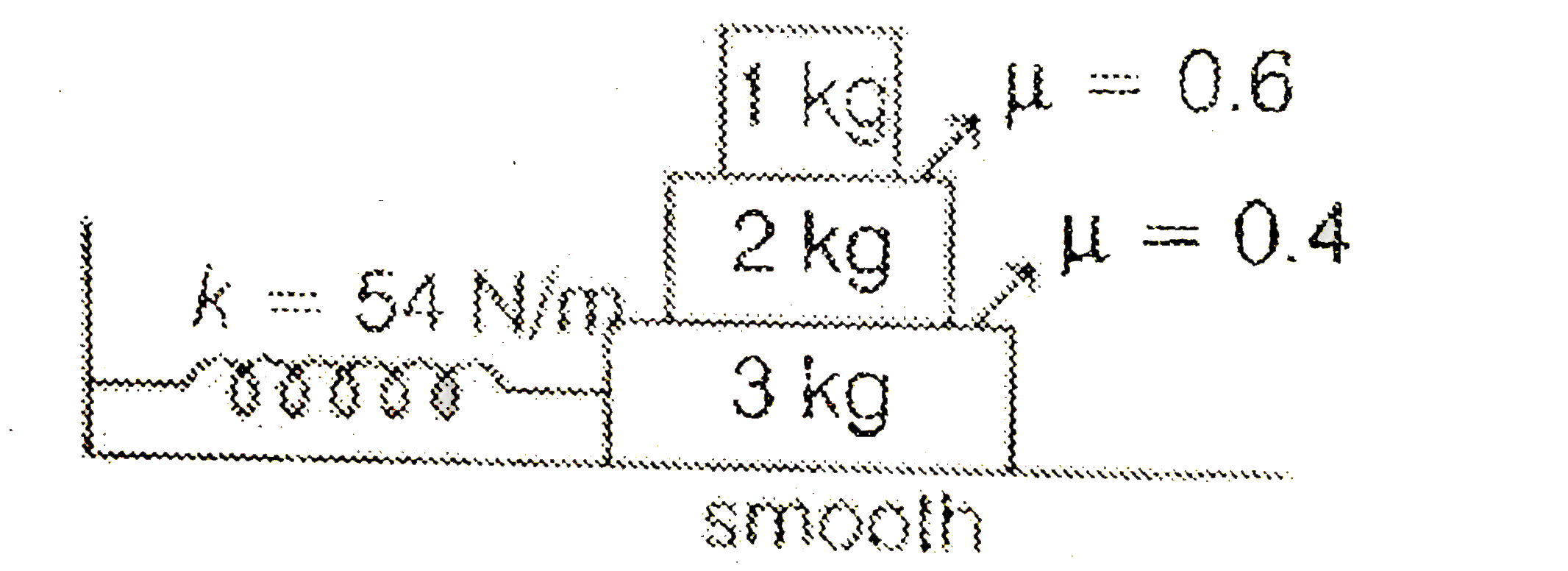
In the figure shown, what can be the maximum amplitude of the system so that there is no slipping between any of hte blocks?A27mB34mC49mD103mFriction between any two surfaces in contact is the force that opposes the relative motion between them The force of limiting friction (F) between any two surfaces in contact is directly proportional to the normal reaction (R) between them F∝R or F=μR where μ is coefficient of limiting friction If θ is angle of friction then μ=tanθ
The acceleration produce in the block in the above question is .A9.8ms−2B0.3ms−2C1.5ms−2D4.9ms−2In the previous question, the angular frequency of the simple harmonic motion is ω. The coefficient of friction between the coin and the platform is μ. The amplitude of oscillation is gradually increased. The coin will begin to slip on the platform for the first time
(i) at the extreme positions of oscillations
(ii) at the mean position
(iii) for an amplitude of μgω2
(iv) for an amplitude of gμω2A(i),(iii)B(ii), (iii)C(i), (iv)D(ii),(iv)
Prism 1 with bar 2 of mass m placed on it gets a horizontal acceleration w directed to the left (figure). At what maximum value of this acceleration will the bar still stationary relative to the prism, if the coefficient of friction between them k<cotα ?

View SolutionA particle of mass 2 kg executing SHM has amplitude 10 cm and time period is 1 s.Find (i) the angular frequency (ii) the maximum speed (ii) the maximum acceleration (iv) the maximum restoring force (v) the speed when the displacement from the mean position is 8 cm (vi) the speed after 112 s the particle was at the extreme position (vii) the time taken by the particle to go directly from its mean position to half the amplitude (viii) the time taken by the particle to go directly from its exterme position to half the amplitude.
View SolutionA body is vibrating with SHM of amplitude 15 cm and frequency 4 Hz. Compute the maximum values of the acceleration and velocity.
View SolutionThe system shown in the figure is in equilibrium The maximum value of W, so that the maximum value of static frictional force on 100kg. body is 450N, will be:
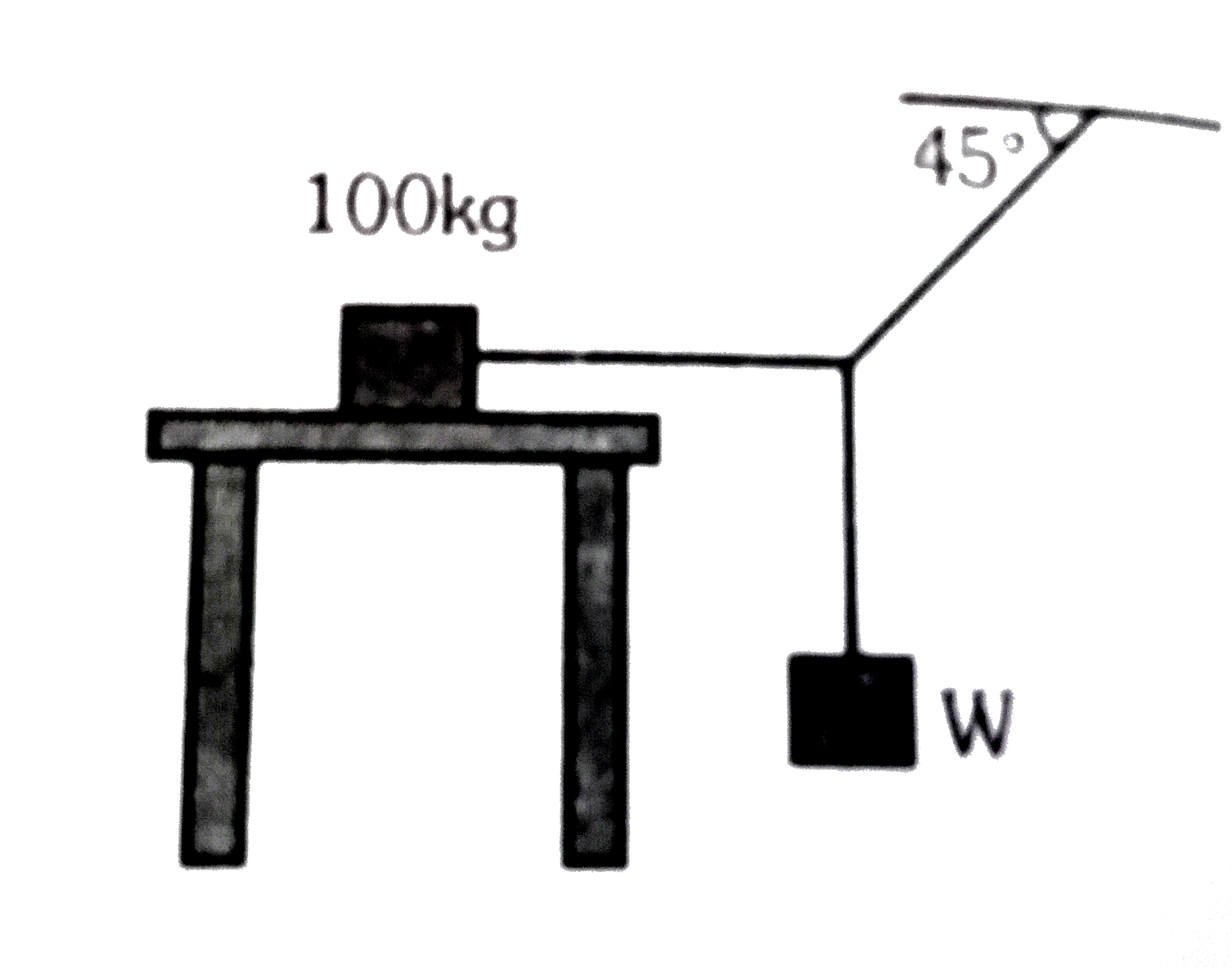
View SolutionThe angular frequency of the damped oscillator is given by ω=√km−r24m2 ,where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio r2/(mk) is 8% ,the change in the time period compared to the undamped oscillator
View Solution

