The angular frequency of the damped oscillator is given by ω=√km−r24m2 ,where k is the spring constant, m is the mass of the oscillator and r is the damping constant. If the ratio r2/(mk) is 8% ,the change in the time period compared to the undamped oscillator
increases by 1%
increases by 8%
decreased by 1%
decrease
The correct Answer is:A
To solve the problem of finding the change in the time period of a damped oscillator compared to an undamped oscillator, we can follow these steps:
Step 1: Understand the given formula for angular frequency
The angular frequency of a damped oscillator is given by:
ω=√km−r24m2
where k is the spring constant, m is the mass, and r is the damping constant.
Step 2: Identify the undamped angular frequency
For an undamped oscillator, the angular frequency is:
ω0=√km
Step 3: Relate the two angular frequencies
We can express the damped angular frequency in terms of the undamped angular frequency:
ω=√km√1−r24mk=ω0√1−r24mk
Step 4: Write the time period equations
The time period T of an oscillator is related to the angular frequency by:
T=2πω
For the undamped oscillator:
T0=2πω0
For the damped oscillator:
T=2πω=2πω0√1−r24mk
Step 5: Find the ratio of the time periods
The ratio of the time periods is given by:
TT0=1√1−r24mk
Step 6: Use the given ratio
We are given that:
r2mk=0.08(8%)
Thus,
r24mk=0.084=0.02
Step 7: Substitute into the time period ratio
Now substituting this into the ratio of the time periods:
TT0=1√1−0.02=1√0.98
Step 8: Calculate the change in time period
Using the approximation for small changes, we can expand √0.98:
√0.98≈1−0.022=1−0.01=0.99
Thus,
TT0≈1.01
This indicates that:
T≈1.01T0
Step 9: Determine the percentage change
The percentage change in the time period is:
Change=(T−T0T0)×100%=(1.01−1)×100%=1%
Conclusion
The change in the time period compared to the undamped oscillator is approximately 1% increase.
---
The angular frequency of a damped oscillator is given by:
ω=√km−r24m2
where k is the spring constant, m is the mass, and r is the damping constant.
For an undamped oscillator, the angular frequency is:
ω0=√km
We can express the damped angular frequency in terms of the undamped angular frequency:
ω=√km√1−r24mk=ω0√1−r24mk
The time period T of an oscillator is related to the angular frequency by:
T=2πω
For the undamped oscillator:
T0=2πω0
For the damped oscillator:
T=2πω=2πω0√1−r24mk
The ratio of the time periods is given by:
TT0=1√1−r24mk
We are given that:
r2mk=0.08(8%)
Thus,
r24mk=0.084=0.02
Now substituting this into the ratio of the time periods:
TT0=1√1−0.02=1√0.98
Using the approximation for small changes, we can expand √0.98:
√0.98≈1−0.022=1−0.01=0.99
Thus,
TT0≈1.01
This indicates that:
T≈1.01T0
The percentage change in the time period is:
Change=(T−T0T0)×100%=(1.01−1)×100%=1%
The change in the time period compared to the undamped oscillator is approximately 1% increase.
Similar Questions
A simple harmonic motion oscillator has two springs of spring constant k and other two of spring constant 2k, arranged as shown in the figure. Calculate the time period of oscillator.
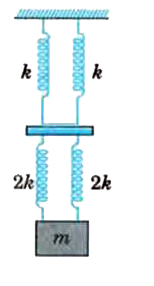
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View Solution
Knowledge Check
A load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
A2π3√10MKB4π√M3KC4π√MKD2π√M3KFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10 g s^(-1) The time period of oscillation is (approx.)
A2πsB2π13sCπ5sDπ√5sA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionThe velocity of the particle of mass m as a function of time t is given by v=Aω.cos[√Kmt] , where A is amplitude of oscillation. The dimension of AK is
View SolutionA spring of spring constant K is cut equal parts of which t part are places in particle and connected will mass m shown in figure The time period of oscilation motion of mass m is
View SolutionFor a damped oscillator the mass 'm' of the block is 200 g, k = 90 N m−1 and the damping constant b is 40 g s−1. Calculate the period of oscillation.
View SolutionA flat spiral spring of force constant k is loaded with mass M and oscillate about vertical with a time period T. Then the mass suspended to the free end is
View Solution

