Passage IV) Angular frequency in SHM is given by ω=√km. Maximum acceleration in SHM is ω2 A and maximum value of friction between two bodies in contact is μN, where N is the normal reaction between the bodies.
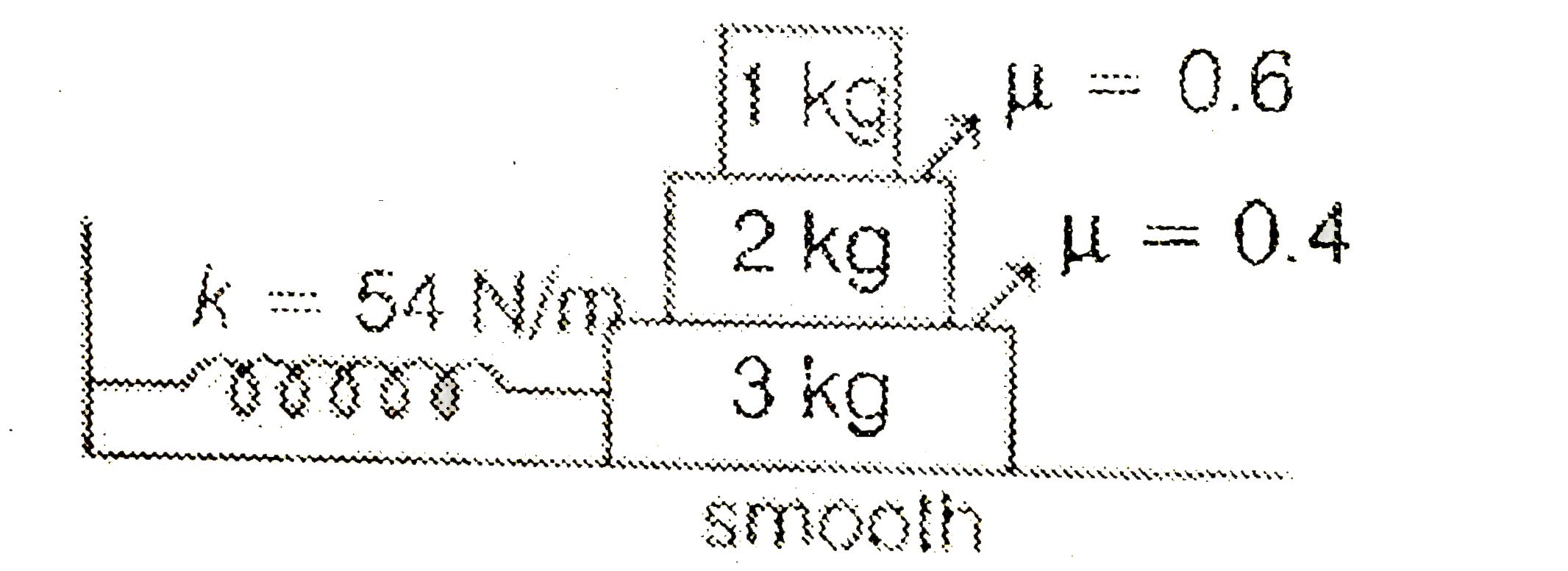
In the figure shown, what can be the maximum amplitude of the system so that there is no slipping between any of hte blocks?
27m
34m
49m
103m
The correct Answer is:C
Step by step video, text & image solution for Passage IV) Angular frequency in SHM is given by omega=sqrt(k/m). Maximum acceleration in SHM is omega^(2) A and maximum value of friction between two bodies in contact is muN, where N is the normal reaction between the bodies. In the figure shown, what can be the maximum amplitude of the system so that there is no slipping between any of hte blocks? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Matrix matching type questions
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Integer type questions
Explore 14 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:More than one option is correct
Explore 50 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionA small block of mass 2 kg is placed on a bigger block of mass 4 kg which is attached to horizontal spring of spring constant K=500N/m as shown in figure, coefficient of friction between block is 0.2 .Maximum amplitude of system so that there is no relative slipping between blocks.
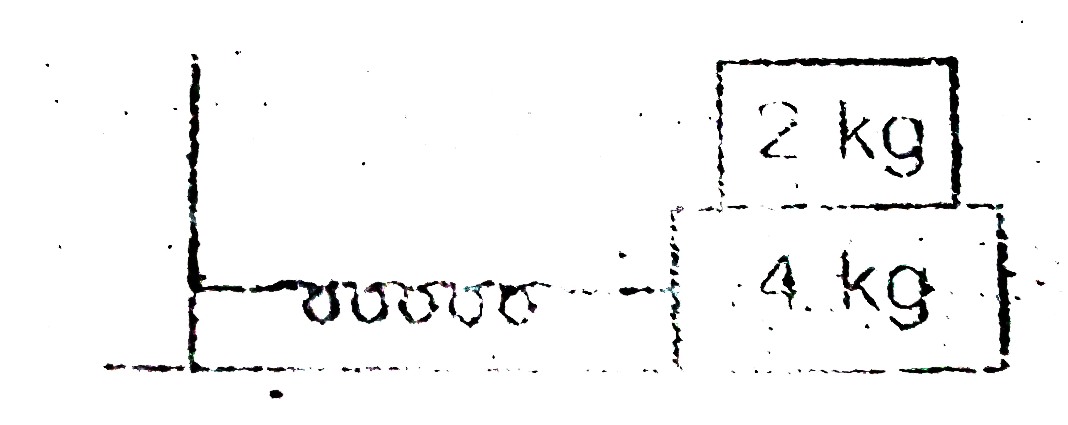
View Solution
Knowledge Check
Passage IV) Angular frequency in SHM is given by ω=√km. Maximum acceleration in SHM is ω2 A and maximum value of friction between two bodies in contact is μN, where N is the normal reaction between the bodies.
Now the value of k, the force constant is increased, then the maximum amplitude calcualted in above question willAremain sameBincreaseCdecreaseDdata is insufficient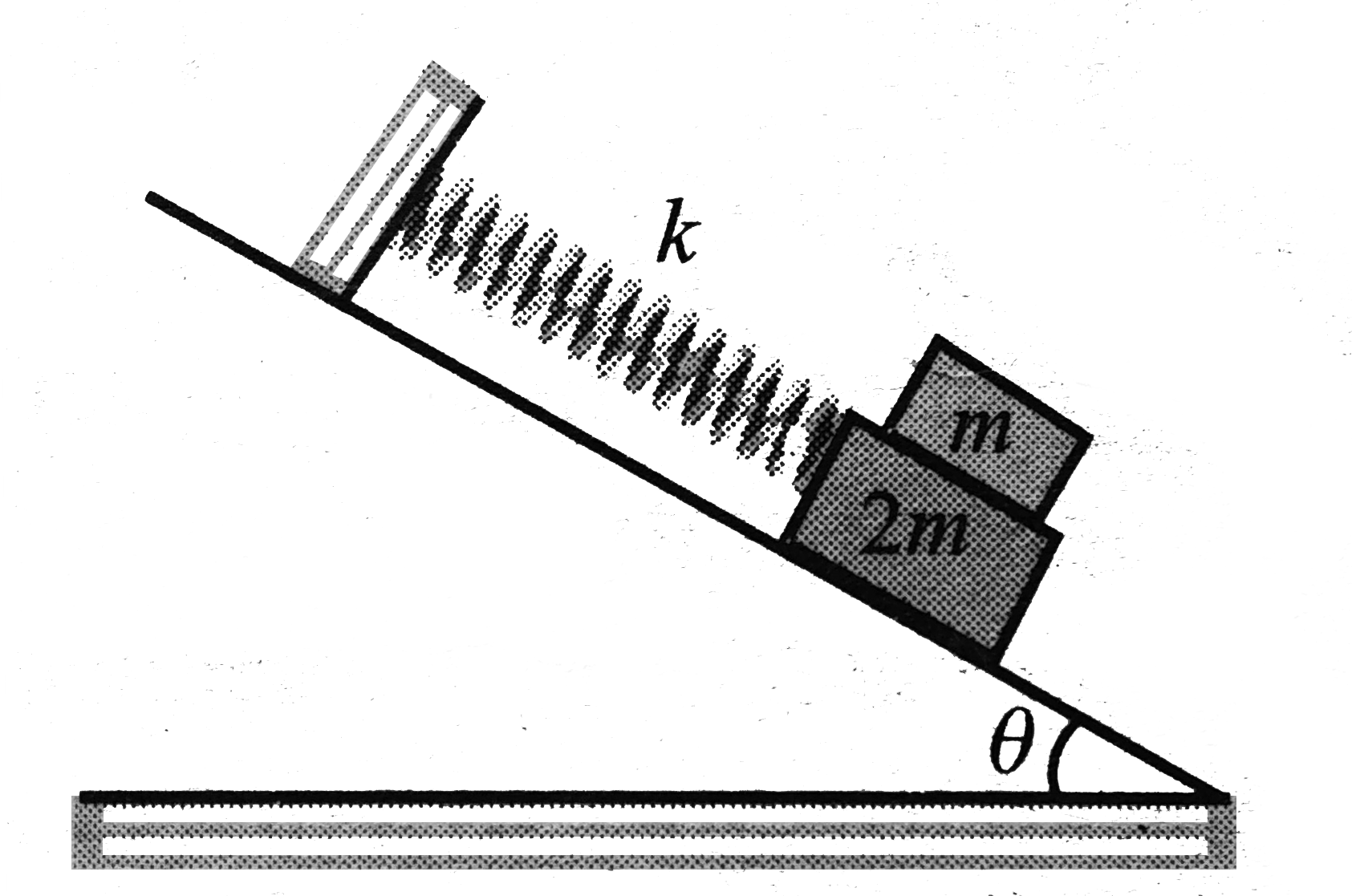
The coefficient of friction between block of mass m and 2m is μ=2tanθ. There is no friction between block of mass 2 m and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks isAgsinθ√kmBmgsinθkC3mgsinθkDnone of theseA block of mass m is at rest on wedge as shown in figure. Let N be the normal reaction between two and f the force of friction, then choose the wrong option.
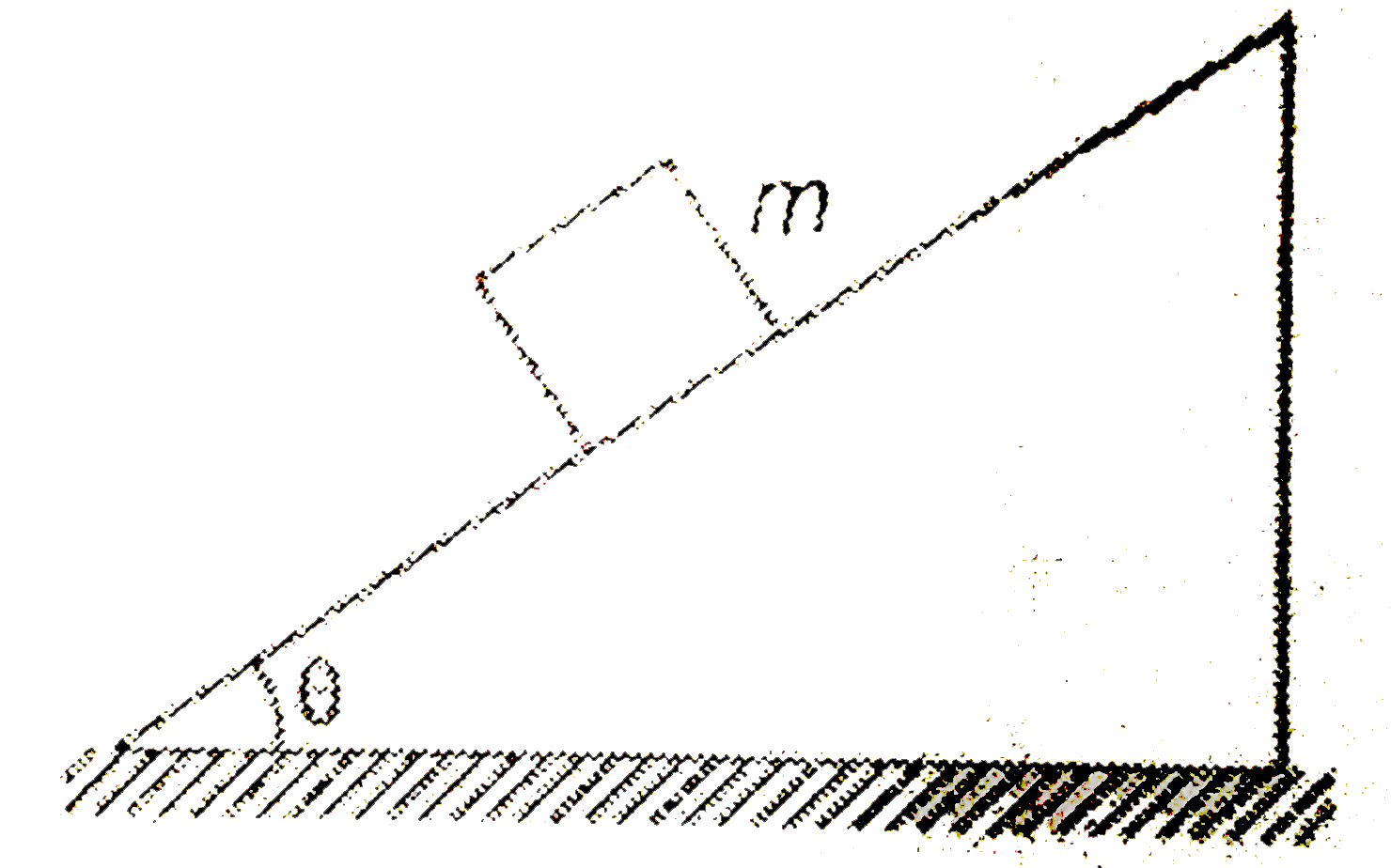 AN=mgcosθBNcosθ+fsinθ=mgCNsinθ=fcosθDNone of these
AN=mgcosθBNcosθ+fsinθ=mgCNsinθ=fcosθDNone of these
A block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View SolutionConsider the situation shown in the figure . The coefficient of friction between the blocks is μ. Find the minimum and the maximum force F that can be applied so that two blocks move together.

View SolutionStatement - 1 : Maximum value of friction force between two surfaces is μ× normal reaction.
where μ = coefficient of friction between surfaces.
Statement - 2 : Friction force between surfaces of two bodies is always less than or equal to externally applied force.
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View SolutionA body is on a rough horizontal surface which is moving horizontally in SHM of frequency 2Hz. The coefficient of static friction between the body and the surface is 0.5. The maximum value of the amplitude for which the body will not slip along the surface is approximately
View Solution

