Consider the situation shown in the figure . The coefficient of friction between the blocks is μ. Find the minimum and the maximum force F that can be applied so that two blocks move together.

F=(M+m)a
a=F(M+m)
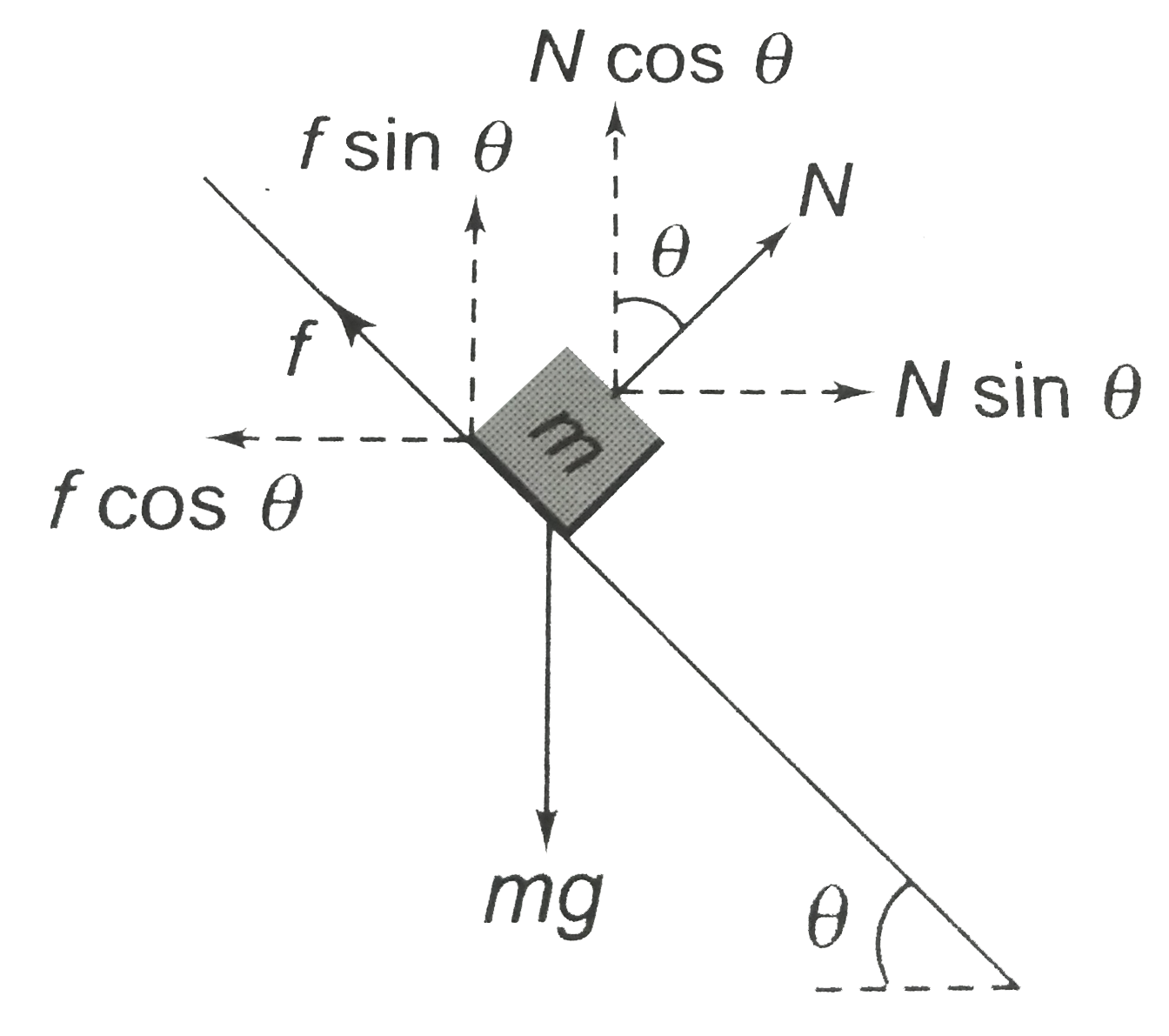
Now consider the block of mass m , if this block has endency to move down , for limiting equilibrium , f=μN.
↑:Ncosθ+fsinθ=mg
Ncosθ+μNsinθ=mg (i)
→:Ncosθ−fcosθ=ma
Nsinθ−μNcosθ=ma (ii)
Dividing (ii) by (i) , we get
ag=sinθ−μcosθcosθ+μsinθ=tanθ−μ1+μtanθ
amin=(tanθ−μ1+μtanθ)g
When large force is applied , the block has tendency to move up , the friction will be in downward direction.
Solving as above
amax=(tanθ+μ1−μtanθ)g
Thus acceleration lies between
(tanθ−μ1+μtanθ)g and (tanθ+μ1−μtanθ)g
Fmin=(M+m)(tanθ−μ1+μtanθ)g
Fmax=(M+m)(tanθ+μ1−μtanθ)g


Topper's Solved these Questions
Similar Questions
Consider the situation as shown in the figgure. The coefficent of friction between the blocks is μ. Find the acceleration of each block.

View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View Solution
Knowledge Check
Consider the situation as shown in the diagram.
The coefficient of friction between the block is 0.5. The acceleration of the lower block isA1m/s2B1.5m/s2C2m/s2D2.5m/s2Consider the situation as shown in the figure.
The maximum value of m so that the blocks do not move is
 A0.2kgB0.4kgC0.6kgD0.8kg
A0.2kgB0.4kgC0.6kgD0.8kgConsider the situation as shown in figure, frictional force acting between surface and 3 kg block is
 A15 NB10 NC0 ND4 N
A15 NB10 NC0 ND4 N
Consider the situation shown in figure. The horizontal surface below the bigger block is smooth. The coefficient of frictioin bewen the blocks is μ. Find the minimum and the maximum force F that can be applied in order to keepthe smaller block at respect to the bigger block.
View SolutionConsider the situation shown in Fig. The hirizontal surface below the bigger block is smooth the coefficient of friction between the block is μ find the minimum and the maximum force F that can be applied in order to keep the smaller blocks at rest with respoct to the bigger block

View SolutionThe coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

View SolutionConsider the situation shwon in Fig. 7.49 . The horizontal surface below the bigger block is smooth . The coefficient of friction between the blocks is μ . Find the minimum and maximum accelerations with which the system should move in order to keep the smaller blocks at rest with respect to the bigger block .

View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View Solution

