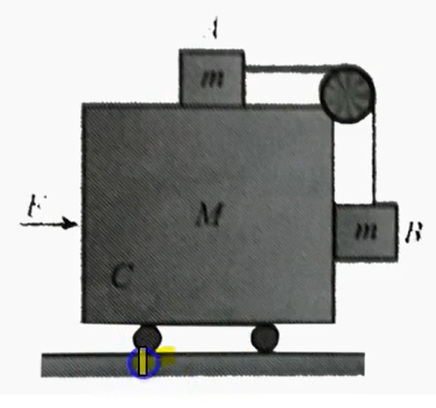
Consider the situation shwon in Fig. 7.49 . The horizontal surface below the bigger block is smooth . The coefficient of friction between the blocks is . Find the minimum and maximum accelerations with which the system should move in order to keep the smaller blocks at rest with respect to the bigger block .

If the system is not accelerated , the block B will pull the block A . Let a be the minimum acceleration , so that A and B are at rest relative to C . As A has a tendency to move towards the pulley ,while B downwards ,so force of friction on A will act away from the pulley while on B upwards .
Now as A is at rest relative to C , so its equation of motion is
or (i)
[as ]
and as block B is at rest relative to C , so for its vertical and horizontal equilibrium , we have
and
or (ii)
Eliminating T between Eqns. (i) and (ii) ,
ma
i .e ., (iii)
Now , if the acceleration of the system is continously increased , there will come a situation when A will have a tendency of slipping away from the pulley P and B upwards . In direction opposite to intended motion , i.e., on A towards pulley while on B downwards so that equations of motion for A and B will become
or
Eliminating T between these,
ma
or
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice
23 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - OBJECTIVE QUESTIONS ( only one choice is correct )
80 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
Consider the situation shown in figure. The horizontal surface below the bigger block is smooth. The coefficient of frictioin bewen the blocks is μ. Find the minimum and the maximum force F that can be applied in order to keepthe smaller block at respect to the bigger block.
View SolutionConsider the situation shown in Fig. The hirizontal surface below the bigger block is smooth the coefficient of friction between the block is μ find the minimum and the maximum force F that can be applied in order to keep the smaller blocks at rest with respoct to the bigger block

View Solution
Knowledge Check
If coefficient of friction between both the block is μ−12 . Find friction force acting between both block.
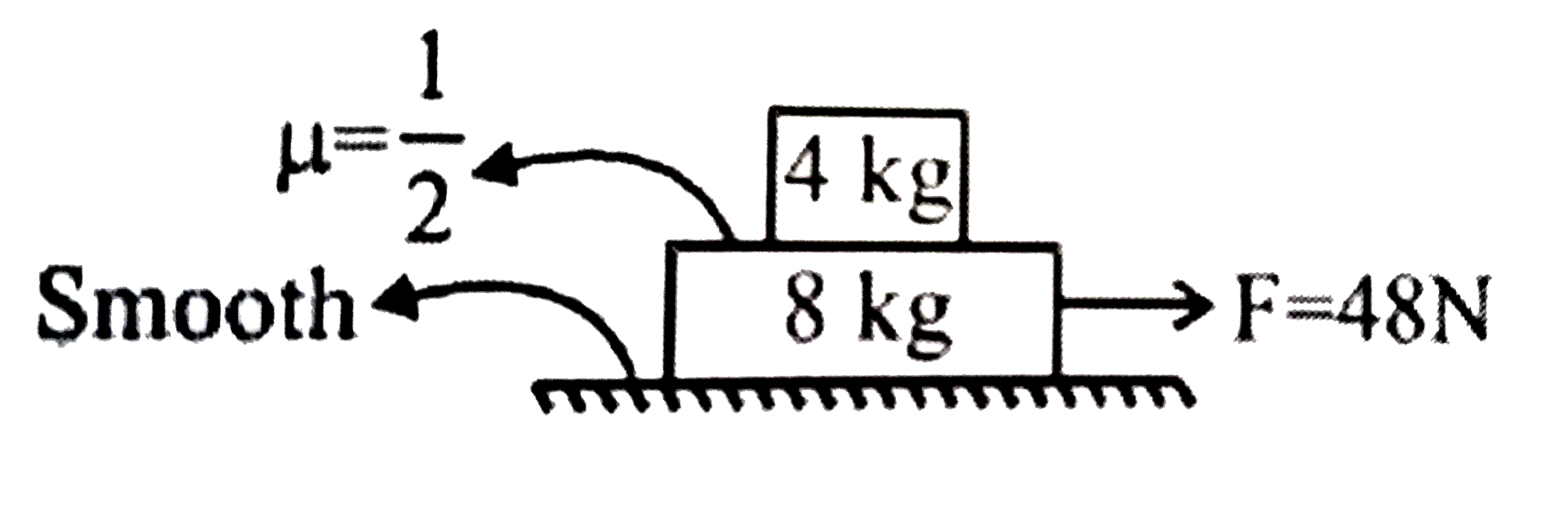 A16NB20NC8ND10N
A16NB20NC8ND10NConsider the situation as shown in the diagram.
The coefficient of friction between the block is 0.5. The acceleration of the lower block isA1m/s2B1.5m/s2C2m/s2D2.5m/s2A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμ
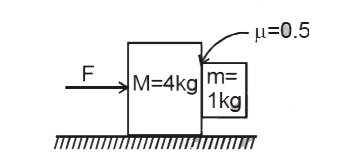
Find out the range of force for which smaller block is at rest with respect to bigger block.
View SolutionConsider the situation as shown in the figgure. The coefficent of friction between the blocks is μ. Find the acceleration of each block.

View SolutionConsider the situation shown in the figure . The coefficient of friction between the blocks is μ. Find the minimum and the maximum force F that can be applied so that two blocks move together.

View SolutionIn the adjoining figure, the coefficient of friction between wedge (of mass M) and block (of mass m) is μ.
Find the minimum horizontal force F required to keep the block stationary with respect to wedge.

View SolutionIn the adjoining figure, the coefficient of friction between wedge ( of mass M) and block ( of mass m) is μ.
Find the minimum horizontal force F rquired to keep the block stationary with respect to wedge

View Solution
