A spring of free length 15 cm is connected to the two masses as shown in the figure −4.149 and compressed 5 cm. The system is released on a smooth horizonal surface. Find the speed of each block when the spring is again at its free length. The force constant for spring is 2100Nm1
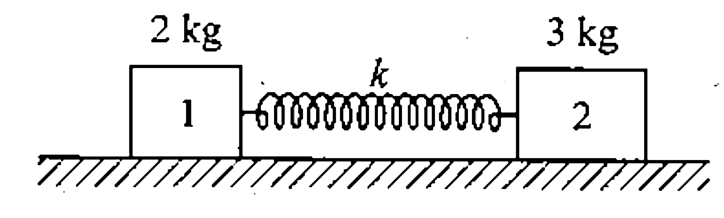
The correct Answer is:[1.575m/s,1.05m/s]
Step by step video, text & image solution for A spring of free length 15 cm is connected to the two masses as shown in the figure -4.149 and compressed 5 cm. The system is released on a smooth horizonal surface. Find the speed of each block when the spring is again at its free length. The force constant for spring is 2100Nm^(1) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:Advance McQ
Explore 20 Videos
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Unsolved Numerical Pro.
Explore 83 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
Similar Questions
The block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
View SolutionTwo blocks of masses m and 2m compress a spring of spring constant k by x0 and blocks are a connected by a thread and placed on a smooth surface as shown. Now , thread is burned. Find the speed of each block when the spring attains its normal length L.
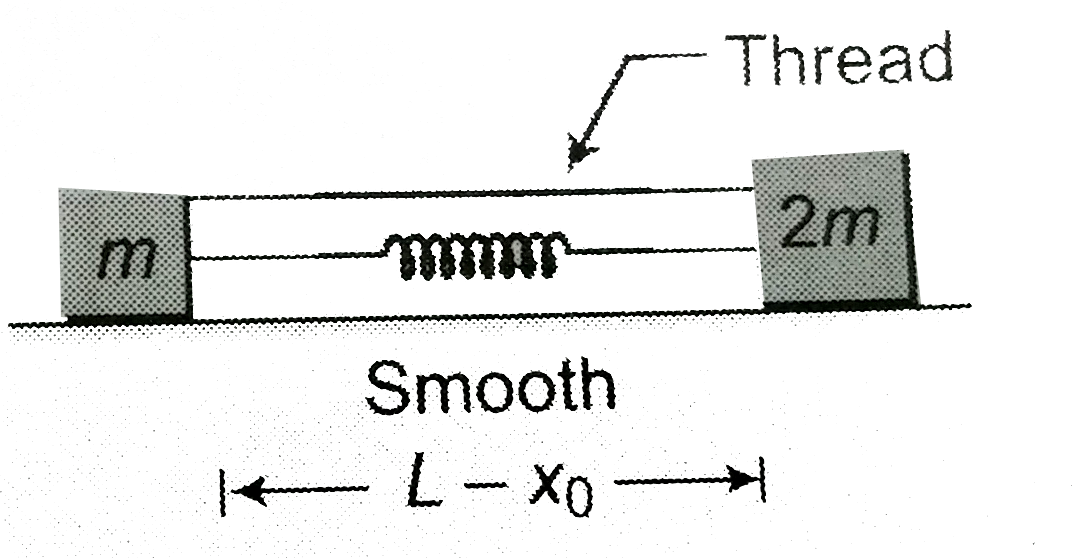
View Solution
Knowledge Check
Two blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
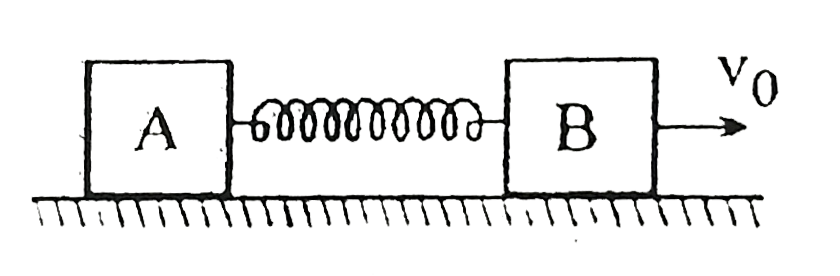 Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at restA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1All surfaces shown in figure are smooth. System is released with the spring unstretched. In equilibrium, compression in the spring will be
 Amg√2KB2mgkC(M+m)g√2kDmgk
Amg√2KB2mgkC(M+m)g√2kDmgk
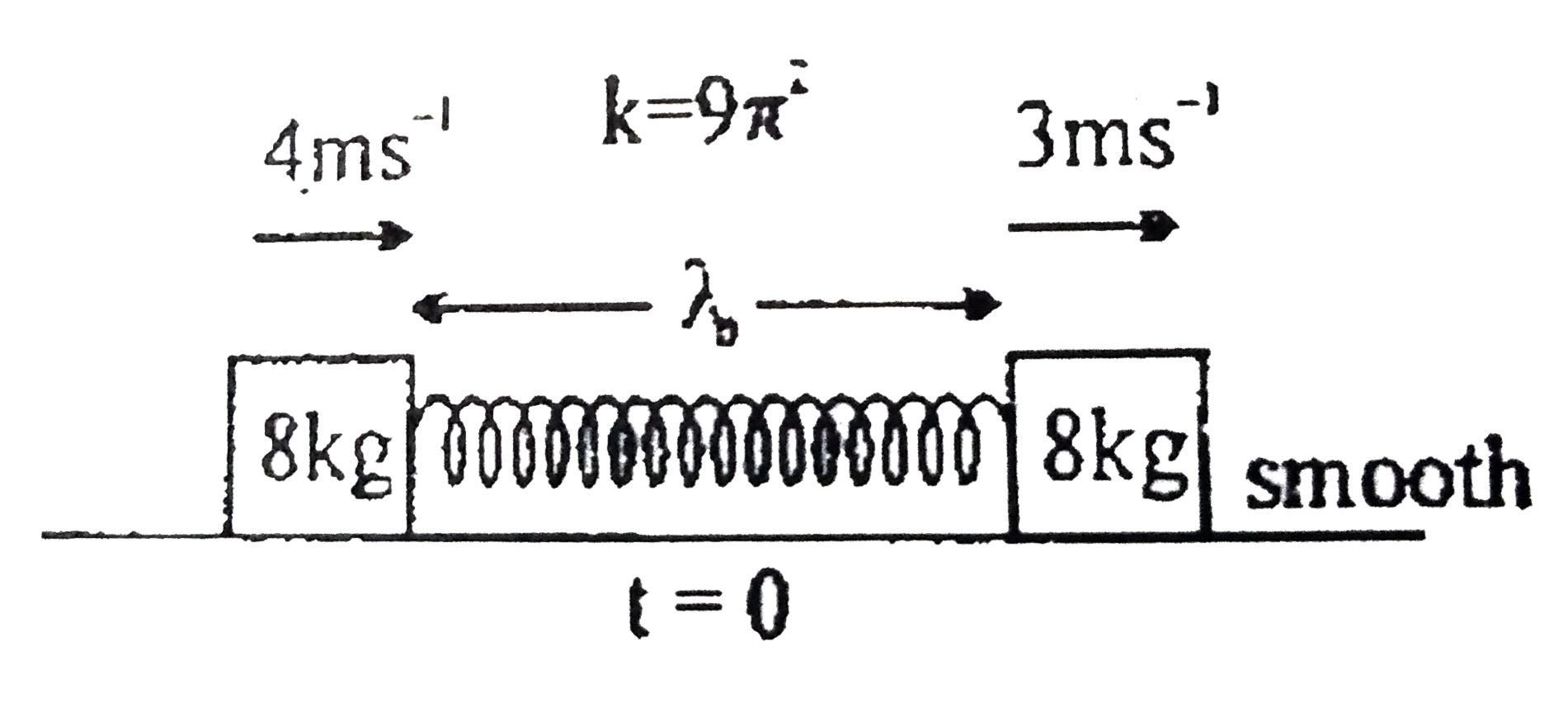
Two block-spring mass system are moving on smooth horizontal surface as shown in the figure as t=0. find out the minimum time t when the spring is maximum elongated l0 is the natural length of spring.
View SolutionTwo blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.

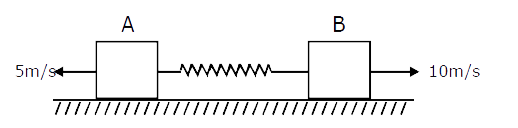
View SolutionThe two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is

View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View Solution

