Two blocks of masses m and 2m compress a spring of spring constant k by x0 and blocks are a connected by a thread and placed on a smooth surface as shown. Now , thread is burned. Find the speed of each block when the spring attains its normal length L.
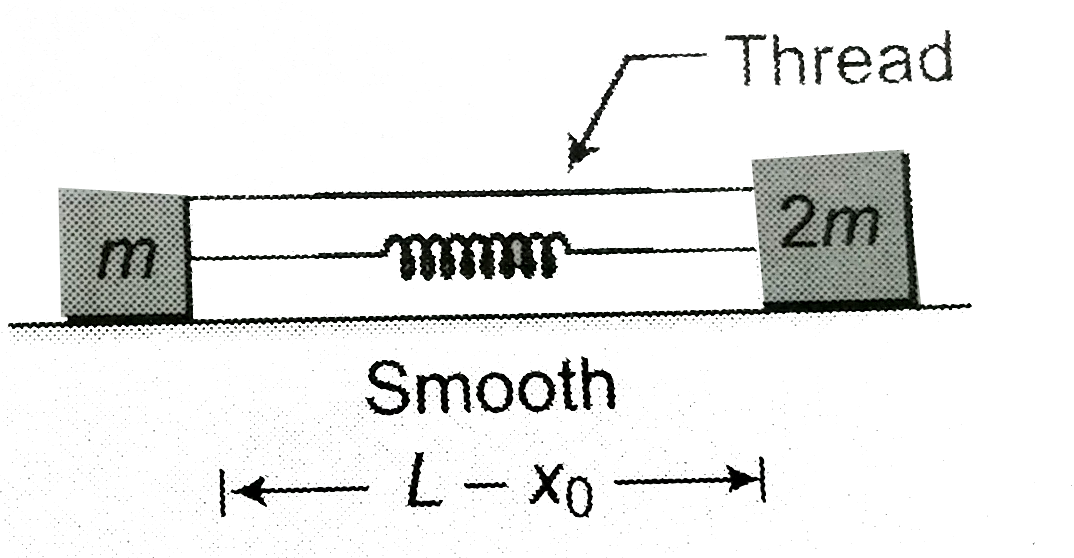
By the momentum conservation
0=−mv1+2mv2⇒v1=2v2
By the energy conservation
12kx20=12mv21+12×2mv22
kx20=m(2v2)2+2mv22=6mv22
v2=√kx206m
v1=2v2=2√kx206m

Topper's Solved these Questions
Similar Questions
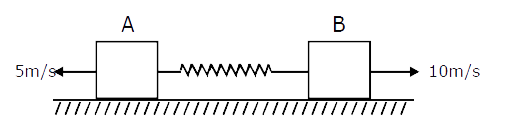
The two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View Solution
Knowledge Check
A block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
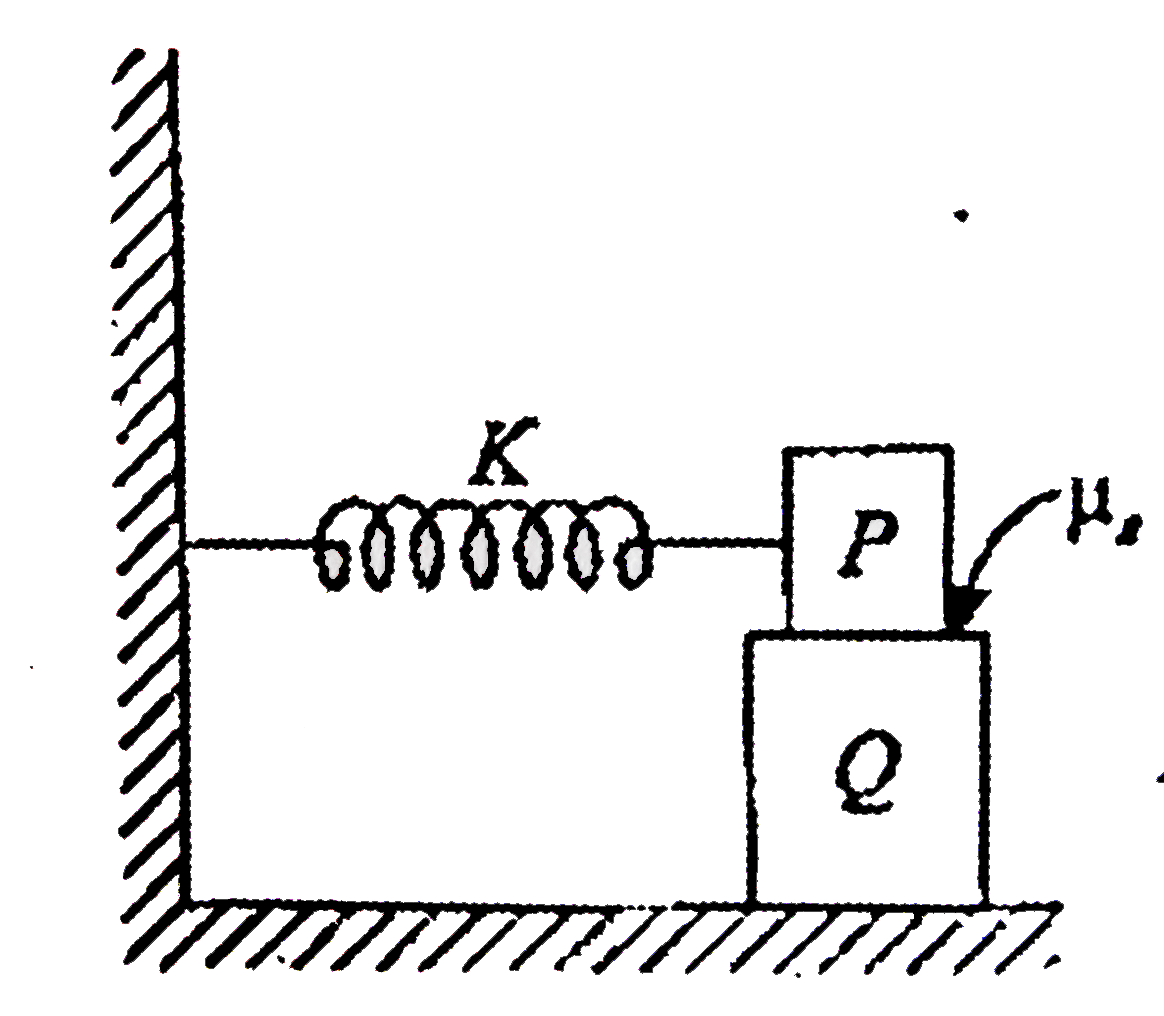 A13KA2B23KA2C12KA2D14KA2
A13KA2B23KA2C12KA2D14KA2A block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
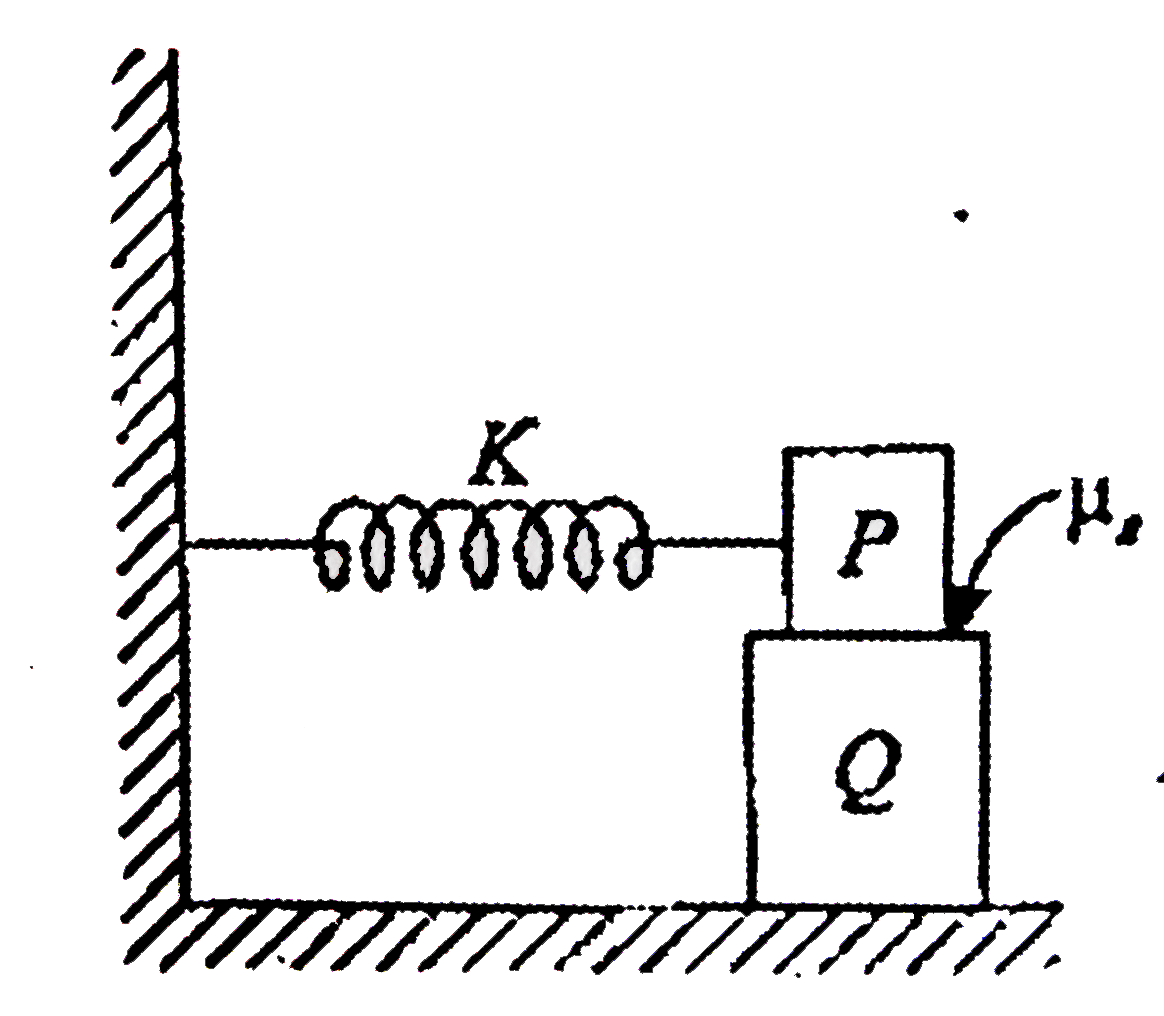 A13KA2B23KA2C12KA2D14KA2
A13KA2B23KA2C12KA2D14KA2Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correct
A block of mass m moving at a speed v0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks of masses m and 2m rest on a frictionless horizontal surface. They are connected by an ideal spring of relaxed length l and stiffness constant k. By means of a massless thread connecting the blocks the spring is held compressed to a length l/2. the whole system is moving with speed v in a direction perpendicular to the length of the spring. the thread is then burnt. Answer the following questions in terms of l,km,v
After burning the string the speed of centre of mass is :
View SolutionTwo blocks of masses m and 2m rest on a frictionless horizontal surface. They are connected by an ideal spring of relaxed length l and stiffness constant k. By means of a massless thread connecting the blocks the spring is held compressed to a length l/2. the whole system is moving with speed v in a direction perpendicular to the length of the spring. the thread is then burnt. Answer the following questions in terms of l,km,v
Before burning, the rato of kinetic energy to potential energy is:
View SolutionTwo blocks of masses m and 2m rest on a frictionless horizontal surface. They are connected by an ideal spring of relaxed length l and stiffness constant k. By means of a massless thread connecting the blocks the spring is held compressed to a length l/2. the whole system is moving with speed v in a direction perpendicular to the length of the spring. the thread is then burnt. Answer the following questions in terms of l,km,v
The time period of oscillation of the system is :
View Solution
