A swimmer wishes to cross a 500m wide river flowing at a rate 5km/hr. His speed with respect to water is 3km/hr. (a) If the heads in a direction making an angle θ with the flow, he takes to cross the river. (b) Find the shortest possible time to cross the river.
The correct Answer is:[(a) 10/sinθ, (b) 10 mins]
To solve the problem step by step, we will break it down into parts as follows:
Step 1: Understand the Problem
We have a river that is 500 meters wide, flowing at a speed of 5 km/hr. The swimmer has a speed of 3 km/hr relative to the water. The swimmer wants to cross the river at an angle θ with respect to the flow of the river.
Step 2: Convert Speeds to SI Units
First, we need to convert the speeds from km/hr to m/s for consistency in units.
- Speed of the river (Vr) = 5 km/hr = 5×10003600 m/s = 50003600 m/s = 2518 m/s.
- Speed of the swimmer (Vs) = 3 km/hr = 3×10003600 m/s = 30003600 m/s = 56 m/s.
Step 3: Break Down the Swimmer's Velocity
The swimmer's velocity can be broken down into two components:
- Vsy=Vssinθ (the component of the swimmer's speed in the direction across the river).
- Vsx=Vscosθ (the component of the swimmer's speed in the direction of the river flow).
Step 4: Calculate Time to Cross the River
The time taken to cross the river is determined by the vertical component of the swimmer's speed:
t=dVsy=500 mVssinθ=50056sinθ=600sinθ seconds.
Step 5: Find the Shortest Possible Time
To minimize the time t, we need to maximize sinθ. The maximum value of sinθ is 1, which occurs when θ=90∘.
- Therefore, the shortest time to cross the river occurs when:
tmin=6001=600 seconds=10 minutes.
Final Answer
(a) The swimmer should head in a direction making an angle θ with the flow, where θ=90∘ for the shortest time.
(b) The shortest possible time to cross the river is 10 minutes.
---
We have a river that is 500 meters wide, flowing at a speed of 5 km/hr. The swimmer has a speed of 3 km/hr relative to the water. The swimmer wants to cross the river at an angle θ with respect to the flow of the river.
First, we need to convert the speeds from km/hr to m/s for consistency in units.
- Speed of the river (Vr) = 5 km/hr = 5×10003600 m/s = 50003600 m/s = 2518 m/s.
- Speed of the swimmer (Vs) = 3 km/hr = 3×10003600 m/s = 30003600 m/s = 56 m/s.
The swimmer's velocity can be broken down into two components:
- Vsy=Vssinθ (the component of the swimmer's speed in the direction across the river).
- Vsx=Vscosθ (the component of the swimmer's speed in the direction of the river flow).
The time taken to cross the river is determined by the vertical component of the swimmer's speed:
t=dVsy=500 mVssinθ=50056sinθ=600sinθ seconds.
To minimize the time t, we need to maximize sinθ. The maximum value of sinθ is 1, which occurs when θ=90∘.
- Therefore, the shortest time to cross the river occurs when:
tmin=6001=600 seconds=10 minutes.
(a) The swimmer should head in a direction making an angle θ with the flow, where θ=90∘ for the shortest time.
(b) The shortest possible time to cross the river is 10 minutes.
Topper's Solved these Questions
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Advance MCQs with One or More Options Correct
Explore 17 Videos
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Unsolved Numerical
Explore 94 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
Similar Questions
A man can swim at a speed of 5km/h in the still water. He wants to cross a 1600m wide river flowing at 4km/h. He keeps himself at an angle 127∘ with the river flow while swimming. (a) Find the time he takes to cross the river. (b) Find the distance traveled by him along the flow.
View SolutionA man can swim at a speed of 3 km/h in still water. He wants t cross a 500 m wide river flowing at 2 km/h. He flow at an angle of 120 with the river flow while swimming. A. Find the time he takes to cross the river. b.At what point on the opposite bank will he arrive?
View Solution
Knowledge Check
A swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
A10minB20minC6minD7.5minA swimmer wishes to .cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angleθ with the perpendicular as shown ip. the. figure.
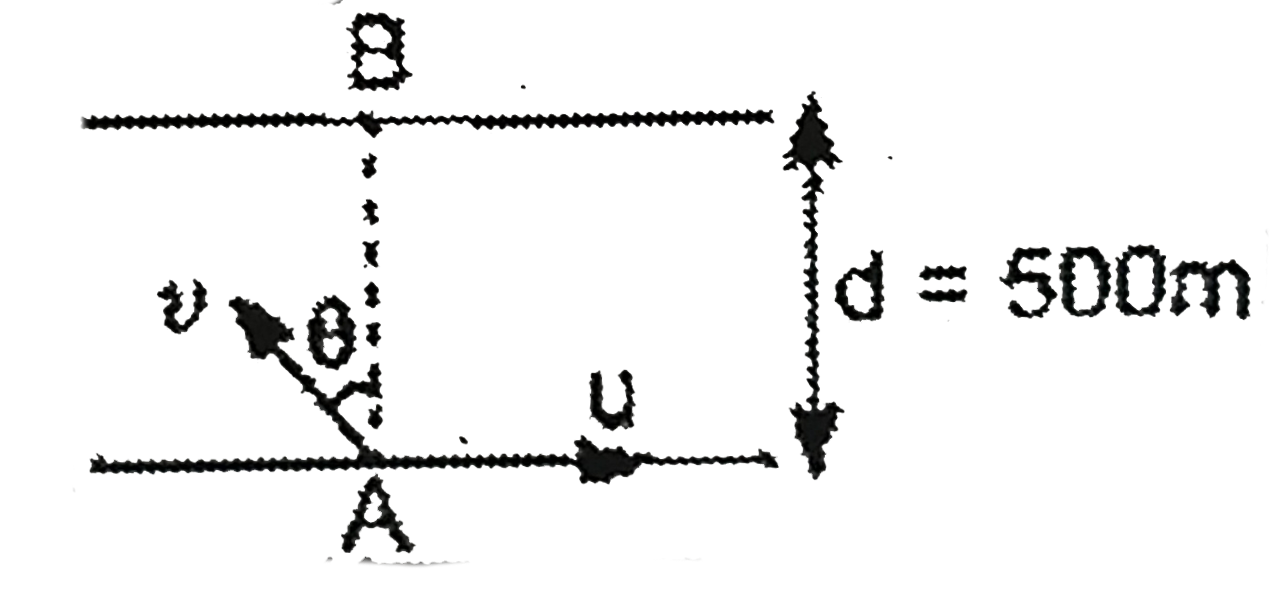
To cross the river in minimum time, the value of θ should be:A0∘B90∘C30∘D60∘A swimmer wishes to cross a river 500m width flowing at a rate u. his speed w.r.t. still water is v. for this he makes an angle θ with the vertical as shown in the given figure then:
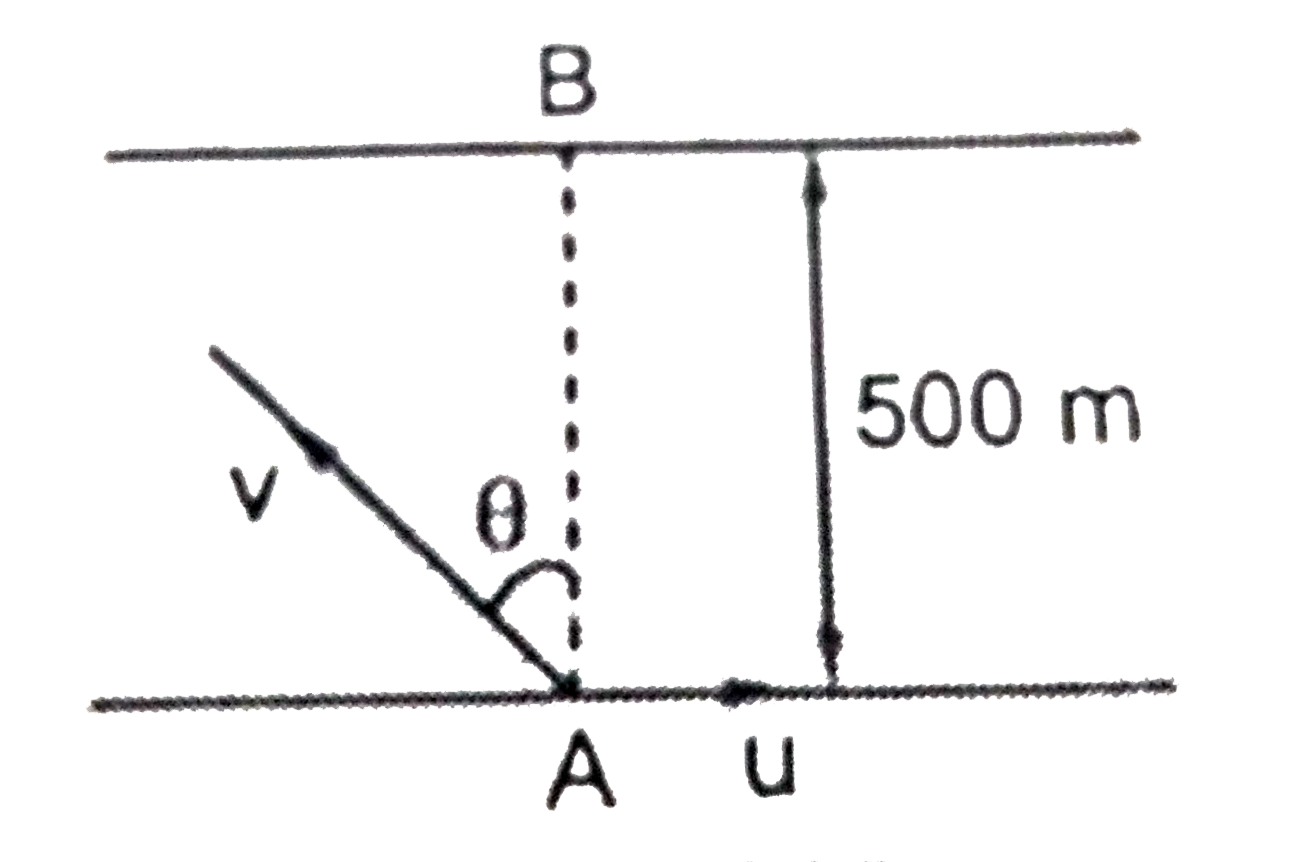 Ato cross the river in minimum time θ=0∘Bto cross the river in minumum time, θ=30∘Cfor u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.Dfor u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.
Ato cross the river in minimum time θ=0∘Bto cross the river in minumum time, θ=30∘Cfor u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.Dfor u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.
A man wishes to cross a river which is flowing at a certain speed . Man uses a motor boat whose velocity with respect to water is more than speed of flow. Minimum possible time the boat takes to cross the river is t1 , but drift along the length of river is x . When boat takes shortest route to cross the river , then it takes time t2 . Find the velocity of boat with respect to water .
View Solution2 km wide river flowing with a rate of 5 km/hr. A man can swim in the still water with10 km/hr. He wants to cross the river along shortest path find
Crossing time
View SolutionA swimmer whishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle θ with the perpendicular as shown in the figure.

For u = 5 km/hrand v=3km//hr, the swimmer :
View SolutionThe stream of a river is flowing with a speed of 2 km/h. A swimmer can swim at a speed of 4 km/h. What should be the direction of the swimmer with respect to the flow of the river to cross the river straight?
View SolutionA river 3m deep and 40m wide is flowing at the rate of 2 km/hr. How much water will fall into the sea in 2 minutes :-
View Solution

