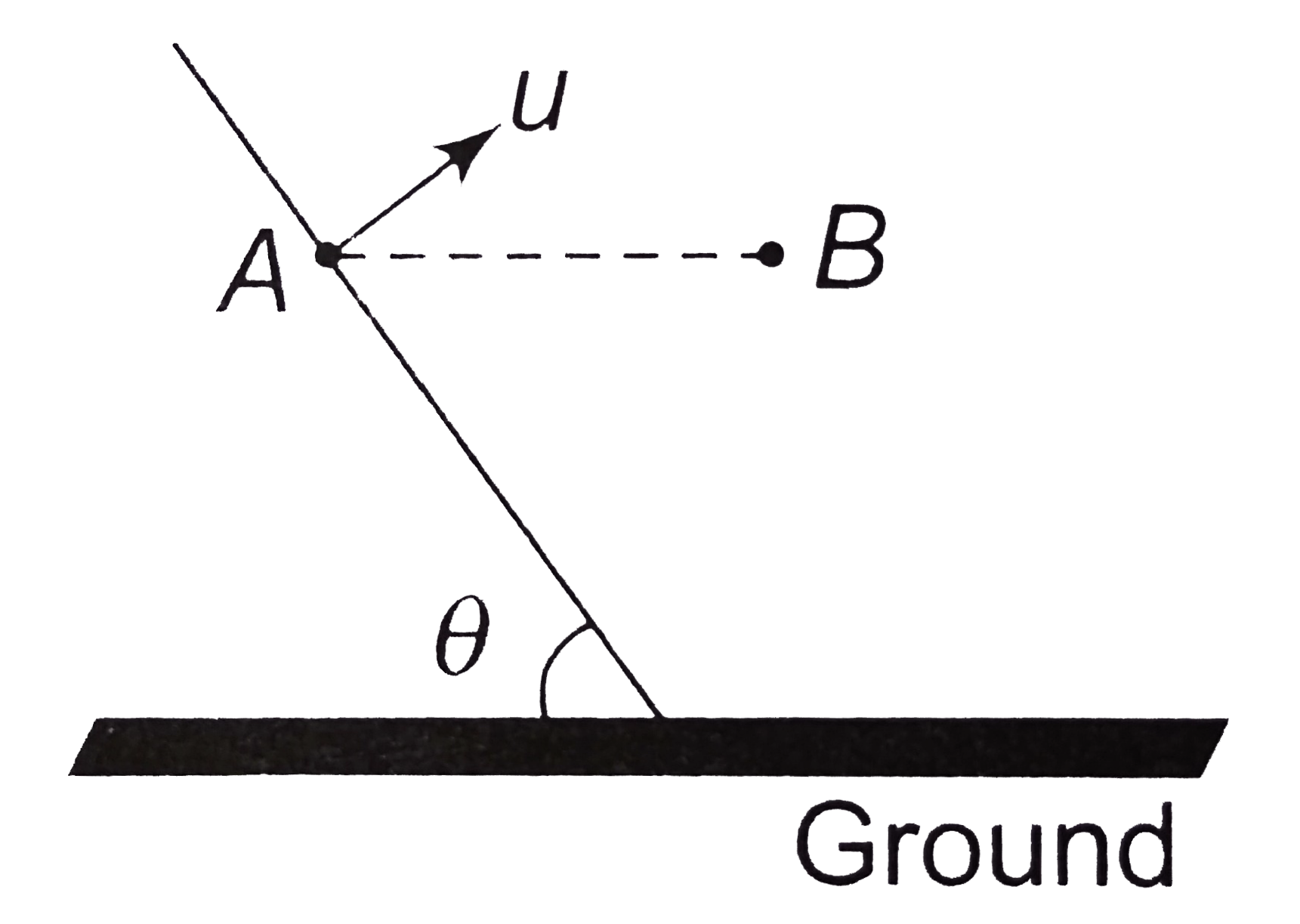
A particle is projected at point A from an inclination plane with inclination angle θ as shown in figure. The magnitude of projection velocity is →u and its direction is perpendicular to the plane. After some time it passes from point B which is in the same horizontal level of A, with velocity →v. Then the angle between →uand→v will be
The correct Answer is:⎡⎢⎣u=[gR(1+3sin2β)2sinβ]1/2⎤⎥⎦
Step by step video, text & image solution for A particle is projected at point A from an inclination plane with inclination angle theta as shown in figure. The magnitude of projection velocity is vecu and its direction is perpendicular to the plane. After some time it passes from point B which is in the same horizontal level of A, with velocity vecv. Then the angle between vecu and vecv will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Advance MCQs with One or More Options Correct
Explore 17 Videos
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Unsolved Numerical
Explore 94 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
Similar Questions
A paricle is projected up from the bottom of an inlined plane of inclination α with velocity v0 If it returns to the points of projection after an elastic impact with the plane, find the total time of motion of the particle.
View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane?
View Solution
Knowledge Check
A ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
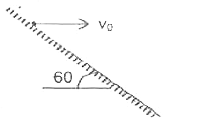 Av0√3gB2v0√3gCv0gD2√3v0g
Av0√3gB2v0√3gCv0gD2√3v0gA particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
Atan(α−β)=cotβB2tan(α−β)=cotβC2cot(α−β)=cotβDNone of theseA particle is projected up an inclined plane with initial speed v=20m/s at an angle θ=30∘ with plane. The component of its velocity perpendicular to plane when it strikes the plane is
A10√3m/sB10m/sC5√3m/sDData is insufficient
A particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α(from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View Solution

