The stream of a river is flowing with a speed of 2 km/h. A swimmer can swim at a speed of 4 km/h. What should be the direction of the swimmer with respect to the flow of the river to cross the river straight?
90∘
60∘
120∘
150∘
The correct Answer is:C
To solve the problem of determining the direction a swimmer should take to cross a river straight while accounting for the river's current, we can follow these steps:
Step 1: Understand the problem
The river is flowing with a speed of 2 km/h, and the swimmer can swim at a speed of 4 km/h. The swimmer wants to cross the river straight, meaning he wants to reach the point directly across from where he started, despite the current pushing him downstream.
Hint: Visualize the situation by drawing a diagram of the river, the swimmer's path, and the current.
Step 2: Set up the vector components
Let the direction across the river (perpendicular to the flow) be the y-direction, and the direction of the river flow be the x-direction. The swimmer's velocity can be broken down into two components:
- Vsy: the component of the swimmer's velocity in the y-direction (across the river).
- Vsx: the component of the swimmer's velocity in the x-direction (against the river flow).
The swimmer's total speed is given as 4 km/h, so we can express this as:
Vs=√V2sx+V2sy
Hint: Remember that the swimmer's speed is the resultant of its components in both directions.
Step 3: Relate the swimmer's speed and the river's speed
To cross the river straight, the swimmer must counteract the river's current. Therefore, the swimmer's x-component of velocity must equal the river's speed:
Vsx=Vr=2 km/h
Step 4: Calculate the y-component of the swimmer's velocity
Using the Pythagorean theorem, we can find the y-component of the swimmer's velocity:
V2s=V2sx+V2sy
Substituting the known values:
42=22+V2sy
16=4+V2sy
V2sy=16−4=12
Vsy=√12=2√3 km/h
Hint: Make sure to keep track of the units and the direction of each component.
Step 5: Determine the angle of swimming
Now, we need to find the angle θ that the swimmer should swim at with respect to the flow of the river. We can use the sine function to relate the components:
sin(θ)=VsxVs=24=12
Thus, we find:
θ=30∘
Hint: Use trigonometric ratios to find the angle, and remember that the angle is measured from the direction of the river flow.
Step 6: Determine the direction with respect to the river
Since the swimmer is swimming at an angle of 30∘ upstream to counter the current, the angle with respect to the direction of the river flow is:
180∘−30∘=150∘
Hint: The angle you find should be measured from the direction of the river flow to ensure it is correct.
Conclusion
The swimmer should swim at an angle of 30∘ upstream from the direction of the river flow to cross the river straight.
Final Answer
The direction of the swimmer with respect to the flow of the river should be 150∘ from the downstream direction.
---
The river is flowing with a speed of 2 km/h, and the swimmer can swim at a speed of 4 km/h. The swimmer wants to cross the river straight, meaning he wants to reach the point directly across from where he started, despite the current pushing him downstream.
Let the direction across the river (perpendicular to the flow) be the y-direction, and the direction of the river flow be the x-direction. The swimmer's velocity can be broken down into two components:
- Vsy: the component of the swimmer's velocity in the y-direction (across the river).
- Vsx: the component of the swimmer's velocity in the x-direction (against the river flow).
Vs=√V2sx+V2sy
To cross the river straight, the swimmer must counteract the river's current. Therefore, the swimmer's x-component of velocity must equal the river's speed:
Vsx=Vr=2 km/h
Using the Pythagorean theorem, we can find the y-component of the swimmer's velocity:
V2s=V2sx+V2sy
Substituting the known values:
42=22+V2sy
16=4+V2sy
V2sy=16−4=12
Vsy=√12=2√3 km/h
Now, we need to find the angle θ that the swimmer should swim at with respect to the flow of the river. We can use the sine function to relate the components:
sin(θ)=VsxVs=24=12
Thus, we find:
θ=30∘
Since the swimmer is swimming at an angle of 30∘ upstream to counter the current, the angle with respect to the direction of the river flow is:
180∘−30∘=150∘
The swimmer should swim at an angle of 30∘ upstream from the direction of the river flow to cross the river straight.
The direction of the swimmer with respect to the flow of the river should be 150∘ from the downstream direction.
Similar Questions
A swimmer can swim in still water with a speed of 2.5 m/s. What is the shortest time taken by him to swim across the river?
View SolutionA swimmer wants to cross a 600 m wide river . If the speed of swimmer is 12 km/hr in still water and speed of river is 6km/hr , along what direction the swimmer must strike in order to cross the river straight ? Also, calculate his resultant velocity and time taken by him to do so .
View Solution
Knowledge Check
A river is flowing due east with a speed 3ms−1. A swimmer can swim in still water at a speed of 4ms−1. If swimmer starts swimming due north, then the resultant velocity of the swimmer is
A3ms−1B5ms−1C7ms−1D2ms−1A river is flowing at a speed of 5 km/h in a particular direction. A man, who can swim at a speed of 20 km/h in still water, starts swimming along the direction of flow of the river from point A and reaches another point B which is at a distance of 30 km from the starting point A. On reaching point B, the man turns back and starts swimming against the direction of flow of the river and stops after reaching point A. The total time taken by the man to complete his journey is
A2 h 30 minB3 h 12 minC3 h 30 minD3 h 45 minA river is flowing at the rate of 6 km/hr. A swimmer swims across with a velocity of 9 km/hr w.r.t. water. The resultant velocity of the man will be in (km/hr):-
A√117B√340C√17D3√40
A man can swim at the rate of 5kmh−1 in still water A. One km wide river flows at the rate of 3kmh−1 . The man wishes to swim across the river directly opposite to the starting point. How much time will be take to cross the river
View SolutionA swimmer wishes to cross a 500m wide river flowing at a rate 5km/hr. His speed with respect to water is 3km/hr. (a) If the heads in a direction making an angle θ with the flow, he takes to cross the river. (b) Find the shortest possible time to cross the river.
View SolutionThe speed of a swimmer with respect to the water is v, the speed of the stream is u. In what direction should the swimmer move to reach the opposite point on the other bank of the river? How long will he swim if the width of the river is l?
View SolutionIf the speed of a swimmer in still water is 9 km/h. Find the down stream speed of the swimmer,whenthe river is flowing with the speed of 6 km/h.
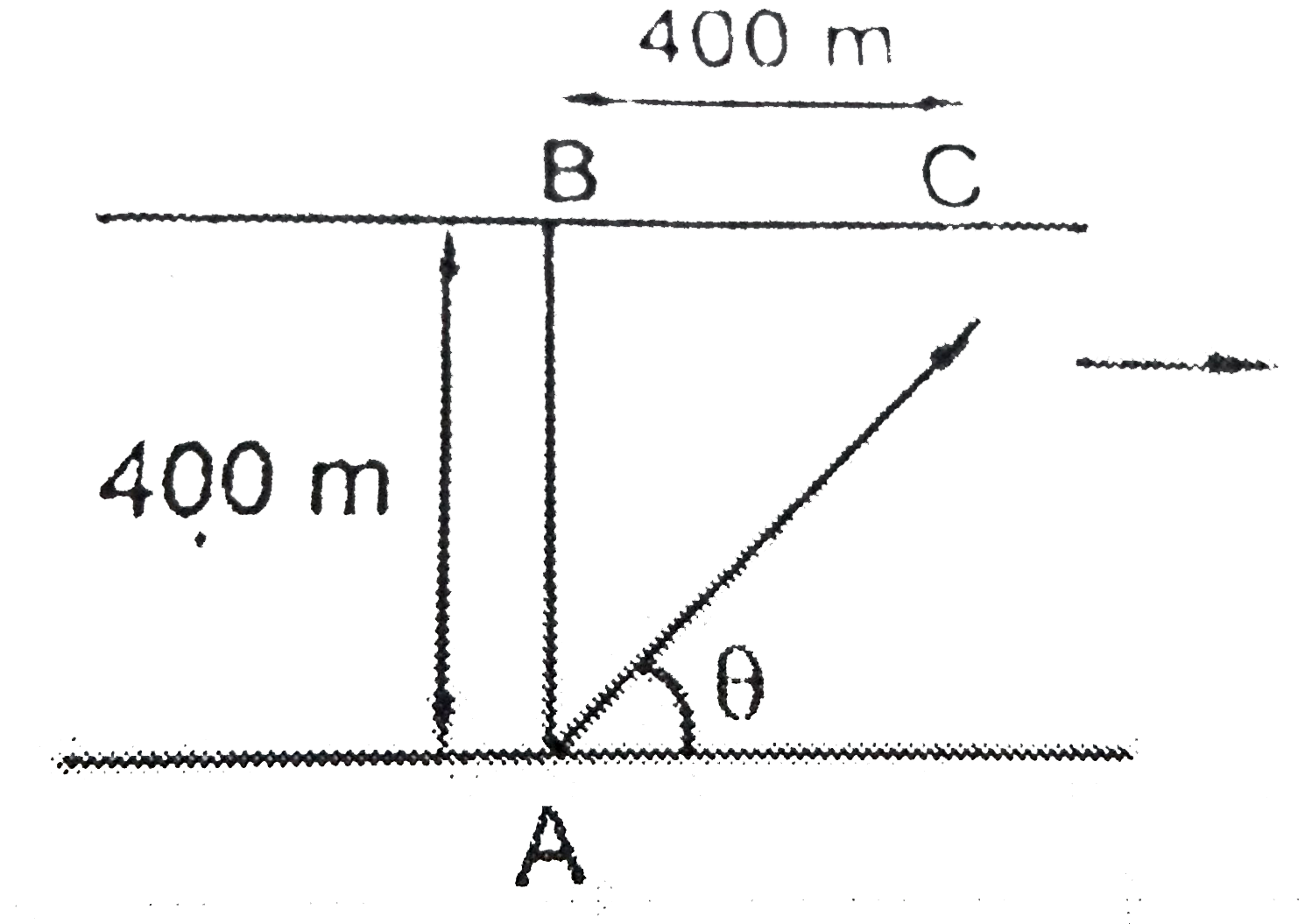
View SolutionA river is flowing with a speed of 1 km/hr. A swimmer wants to go to point C starting from A. He swims with a speed of 5km/hr. at an angle θ. W.r.t. the river flow. If AB=BC=400m at what angle with river tank shou ld swimmer swim?
View Solution

