A bird flies for 4s with a velocity V=(t−2)m/s in a straight line where t= time in second Calculate the displacement and distance covered by the bird
To solve the problem, we need to calculate both the displacement and the distance covered by the bird that flies with a velocity given by V=(t−2) m/s for a duration of 4 seconds.
Step 1: Understand the velocity function
The velocity of the bird is given as:
V(t)=t−2
This means that the velocity changes with time.
Step 2: Find the time intervals for the velocity
To analyze the motion, we need to determine when the velocity is zero:
t−2=0
t=2 seconds
This indicates that the bird changes direction at t=2 seconds.
Step 3: Calculate the displacement
The displacement s can be calculated using the integral of the velocity function over the time interval from 0 to 4 seconds:
s=∫40V(t)dt=∫40(t−2)dt
Step 4: Evaluate the integral
Calculating the integral:
s=∫40(t−2)dt=(t22−2t)40
Now substituting the limits:
s=(422−2×4)−(022−2×0)
s=(162−8)−0
s=(8−8)=0 meters
Step 5: Calculate the distance covered
To find the distance, we need to consider the motion in two segments: from t=0 to t=2 seconds (where the velocity is negative) and from t=2 to t=4 seconds (where the velocity is positive).
1. From t=0 to t=2:
Distance=∫20|V(t)|dt=∫20(2−t)dt
=(2t−t22)20=(2×2−222)−0
=(4−2)=2 meters
2. From t=2 to t=4:
Distance=∫42V(t)dt=∫42(t−2)dt
=(t22−2t)42
=(422−2×4)−(222−2×2)
=(8−8)−(2−4)=0+2=2 meters
Step 6: Total distance covered
Now, adding both segments:
Total Distance=2+2=4 meters
Final Results
- Displacement: 0 meters
- Distance Covered: 4 meters
The velocity of the bird is given as:
V(t)=t−2
This means that the velocity changes with time.
To analyze the motion, we need to determine when the velocity is zero:
t−2=0
t=2 seconds
This indicates that the bird changes direction at t=2 seconds.
The displacement s can be calculated using the integral of the velocity function over the time interval from 0 to 4 seconds:
s=∫40V(t)dt=∫40(t−2)dt
Calculating the integral:
s=∫40(t−2)dt=(t22−2t)40
Now substituting the limits:
s=(422−2×4)−(022−2×0)
s=(162−8)−0
s=(8−8)=0 meters
To find the distance, we need to consider the motion in two segments: from t=0 to t=2 seconds (where the velocity is negative) and from t=2 to t=4 seconds (where the velocity is positive).
Distance=∫20|V(t)|dt=∫20(2−t)dt
=(2t−t22)20=(2×2−222)−0
=(4−2)=2 meters
Distance=∫42V(t)dt=∫42(t−2)dt
=(t22−2t)42
=(422−2×4)−(222−2×2)
=(8−8)−(2−4)=0+2=2 meters
Now, adding both segments:
Total Distance=2+2=4 meters
- Displacement: 0 meters
- Distance Covered: 4 meters
Topper's Solved these Questions
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-1
Explore 86 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-2
Explore 25 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-3
Explore 34 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
Similar Questions
A bird flies for 4s with a velcoty v=t (-2) ms^(-1) in a stralght line. Calculate the displacement of the bird ans distance travelled by the bird.
View SolutionA particle is moving along the x-axis such that s=6t−t2, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5s.
View Solution
Knowledge Check
A bird flies for 4 sec with a velocity of |t−2| m/s in a straight line, where t= time in seconds. It covers a distance of :
A2mB4mC6mD8mA bird flies for 4 seconds with a velocity of |t−2|m/sec. In a straight line, where t= time in seconds. It covers a distance of
A4mB6mC8mDnone of theseA bird flies to and fro between two cars which moves with velocities v1=20m/sandv2=30m/s. If the speed of the bird is v3=10m/s and the initial distance of separation between them is d=2km, find the total distance covered by the bird till the cars meet.
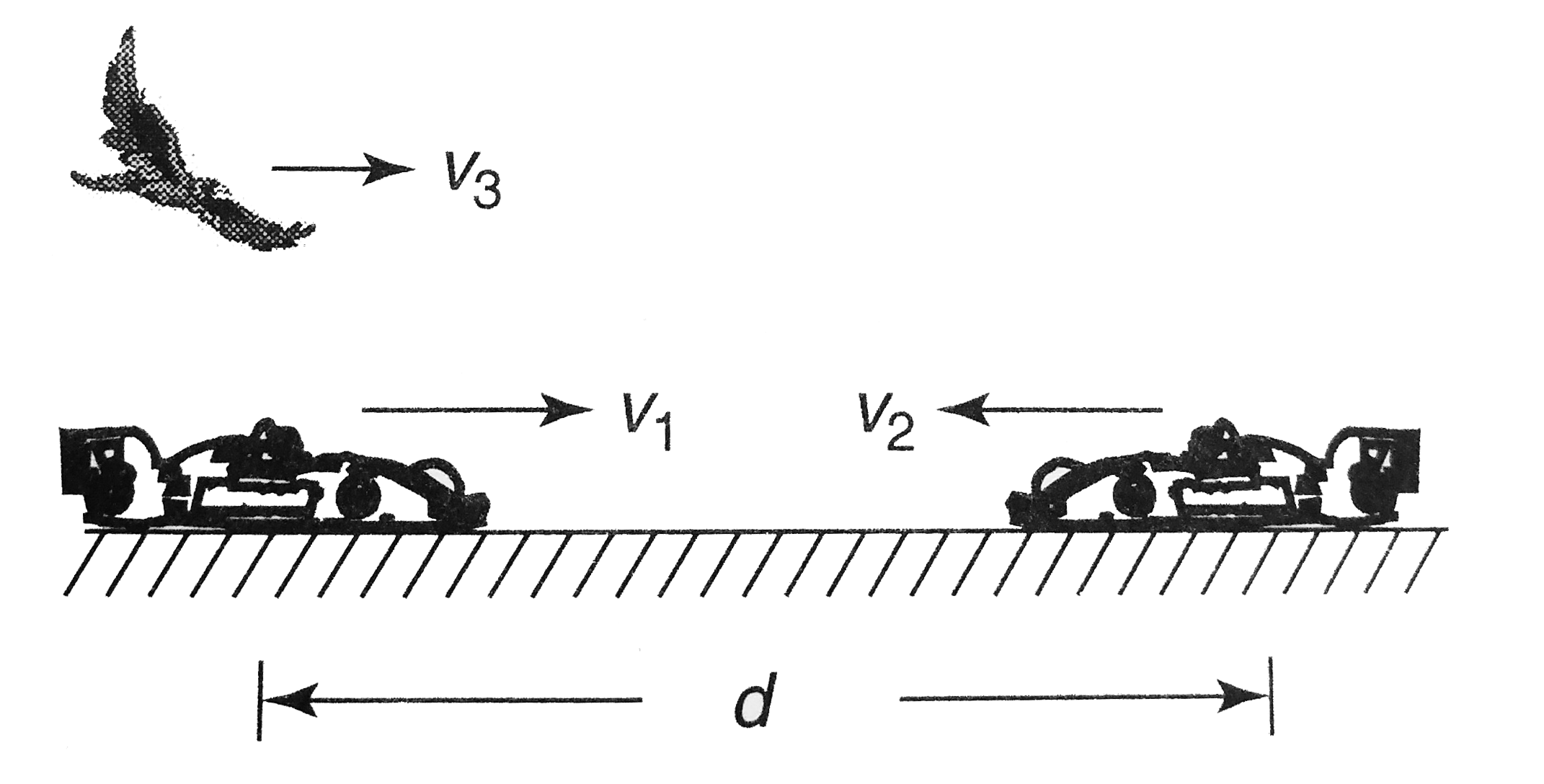 A2000 mB1000 mC400 mD200 m
A2000 mB1000 mC400 mD200 m
Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionThe velocity (u)-time (t) graph of an object moving along a straight line is as shown is Fig. 2 (b) . 30. Calculate the distance covered by object between (i)t=0→t=5s (ii) t=0→t=10s.
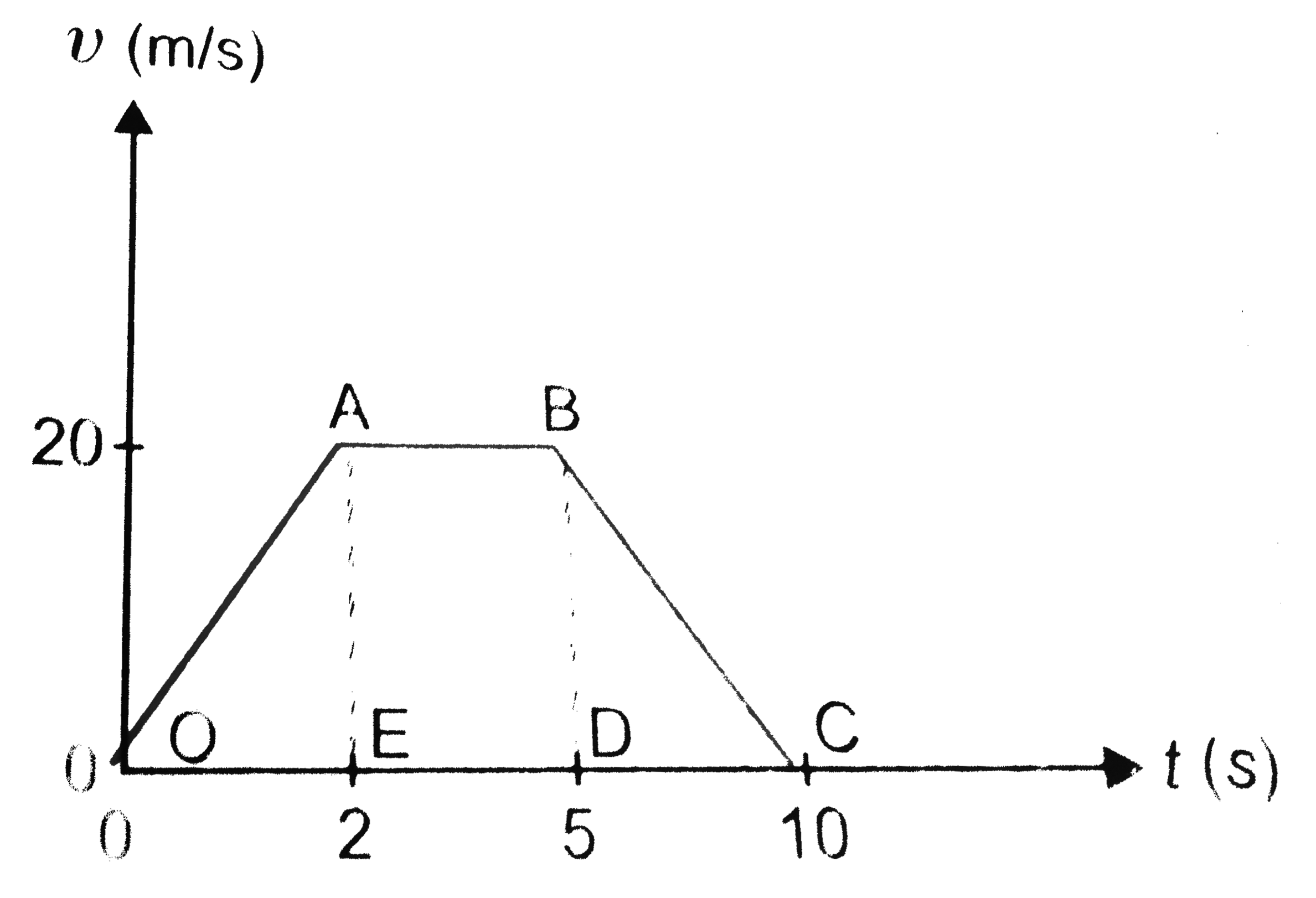 .
.
View SolutionThe velocity (u)-time (t) graph of an object moving along a straight line is as shown is Fig. 2 (b) . 30. Calculate the distance covered by object between (i)t=0→t=5s (ii) t=0→t=10s.
 .
.
View SolutionThe velocity-tiem graph of a particle movitgn along a straight line is shown in the Fig. 2 ( b) . 34becurve OABCD.Calca––tethedistancecoveredbythepartic≤between(i) t =zero to t=18seconds(ii)t=2s→t=12s. And the maximum value of acceleration during this interval.
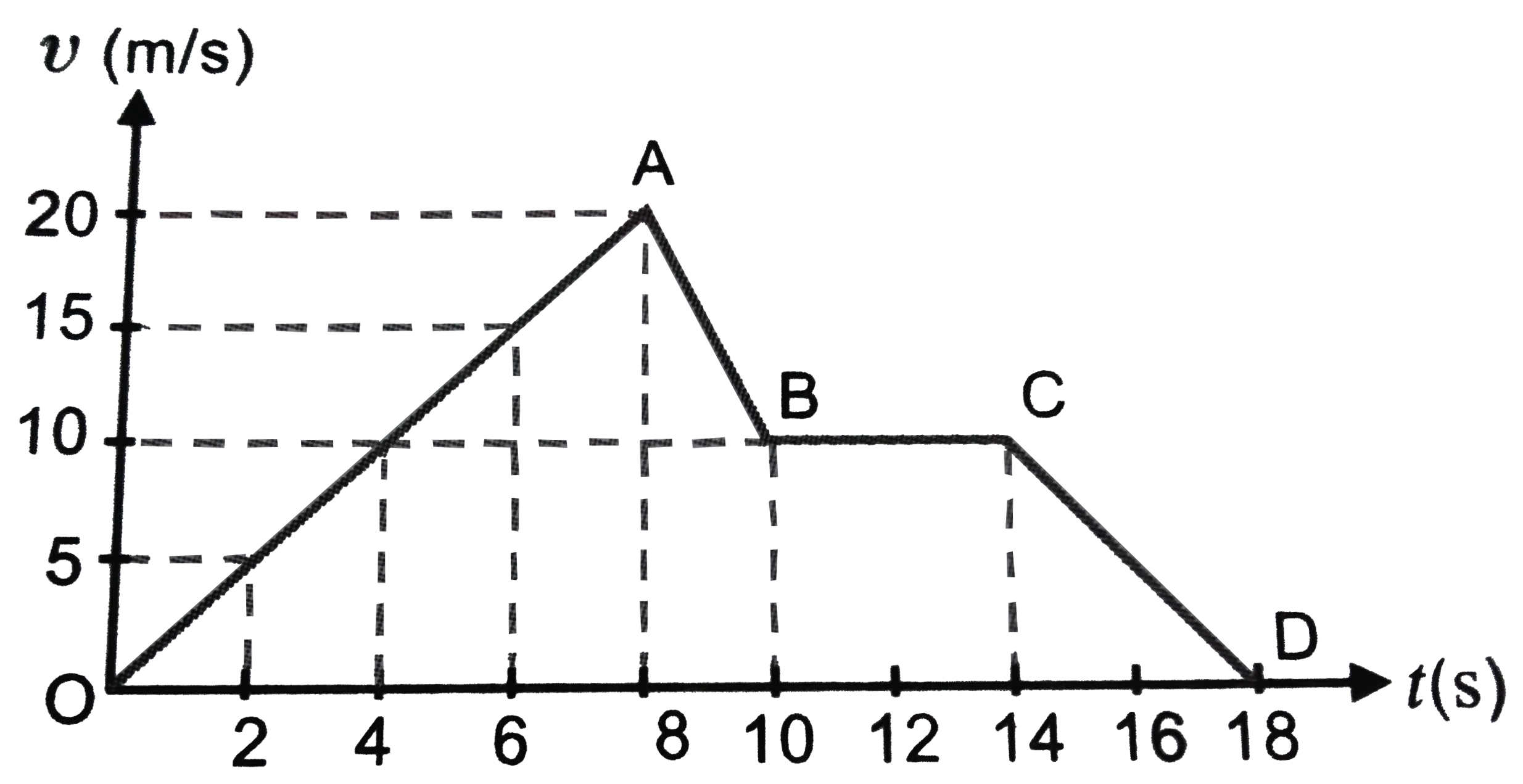 .
.
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View Solution

