A particle is moving along the x-axis such that s=6t−t2, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5s.
To solve the problem, we need to find both the displacement and the distance traveled by the particle during the time interval from t=0 to t=5 seconds, given the displacement function s=6t−t2.
1. Find Displacement at t=0:
s(0)=6(0)−(0)2=0 meters
2. Find Displacement at t=5:
s(5)=6(5)−(5)2=30−25=5 meters
3. Calculate Total Displacement:
The total displacement from t=0 to t=5 seconds is:
Δs=s(5)−s(0)=5−0=5 meters
4. Find Velocity:
The velocity v is the derivative of displacement with respect to time:
v(t)=dsdt=ddt(6t−t2)=6−2t
5. Find When Velocity is Zero:
Set the velocity equation to zero to find when the particle changes direction:
6−2t=0⟹2t=6⟹t=3 seconds
6. Calculate Displacement from t=0 to t=3:
s(3)=6(3)−(3)2=18−9=9 meters
7. Calculate Displacement from t=3 to t=5:
s(5)=5 meters (already calculated)
The displacement from t=3 to t=5 is:
Δs3→5=s(5)−s(3)=5−9=−4 meters
Since we are interested in distance, we take the absolute value:
Distance from t=3 to t=5=4 meters
8. Calculate Total Distance Traveled:
The total distance traveled is the sum of the distances from t=0 to t=3 and from t=3 to t=5:
Distance=Δs0→3+Δs3→5=9+4=13 meters
Final Results:
- Total Displacement: 5 meters
- Total Distance Traveled: 13 meters
s(0)=6(0)−(0)2=0 meters
s(5)=6(5)−(5)2=30−25=5 meters
The total displacement from t=0 to t=5 seconds is:
Δs=s(5)−s(0)=5−0=5 meters
The velocity v is the derivative of displacement with respect to time:
v(t)=dsdt=ddt(6t−t2)=6−2t
Set the velocity equation to zero to find when the particle changes direction:
6−2t=0⟹2t=6⟹t=3 seconds
s(3)=6(3)−(3)2=18−9=9 meters
s(5)=5 meters (already calculated)
The displacement from t=3 to t=5 is:
Δs3→5=s(5)−s(3)=5−9=−4 meters
Since we are interested in distance, we take the absolute value:
Distance from t=3 to t=5=4 meters
The total distance traveled is the sum of the distances from t=0 to t=3 and from t=3 to t=5:
Distance=Δs0→3+Δs3→5=9+4=13 meters
- Total Displacement: 5 meters
- Total Distance Traveled: 13 meters
Topper's Solved these Questions
Similar Questions
An object moves along x-axis such that its position varies with time according to the relation x=50t−5t2
Here, x is in meters and time is in seconds. Find the displacement and distance travelled for the time interval t = 0 to t = 6 s.
View SolutionA particle is moving such that s=t3−6t2+18t+9, where s is in meters and t is in meters and t is in seconds. Find the minimum velocity attained by the particle.
View Solution
Knowledge Check
Figure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
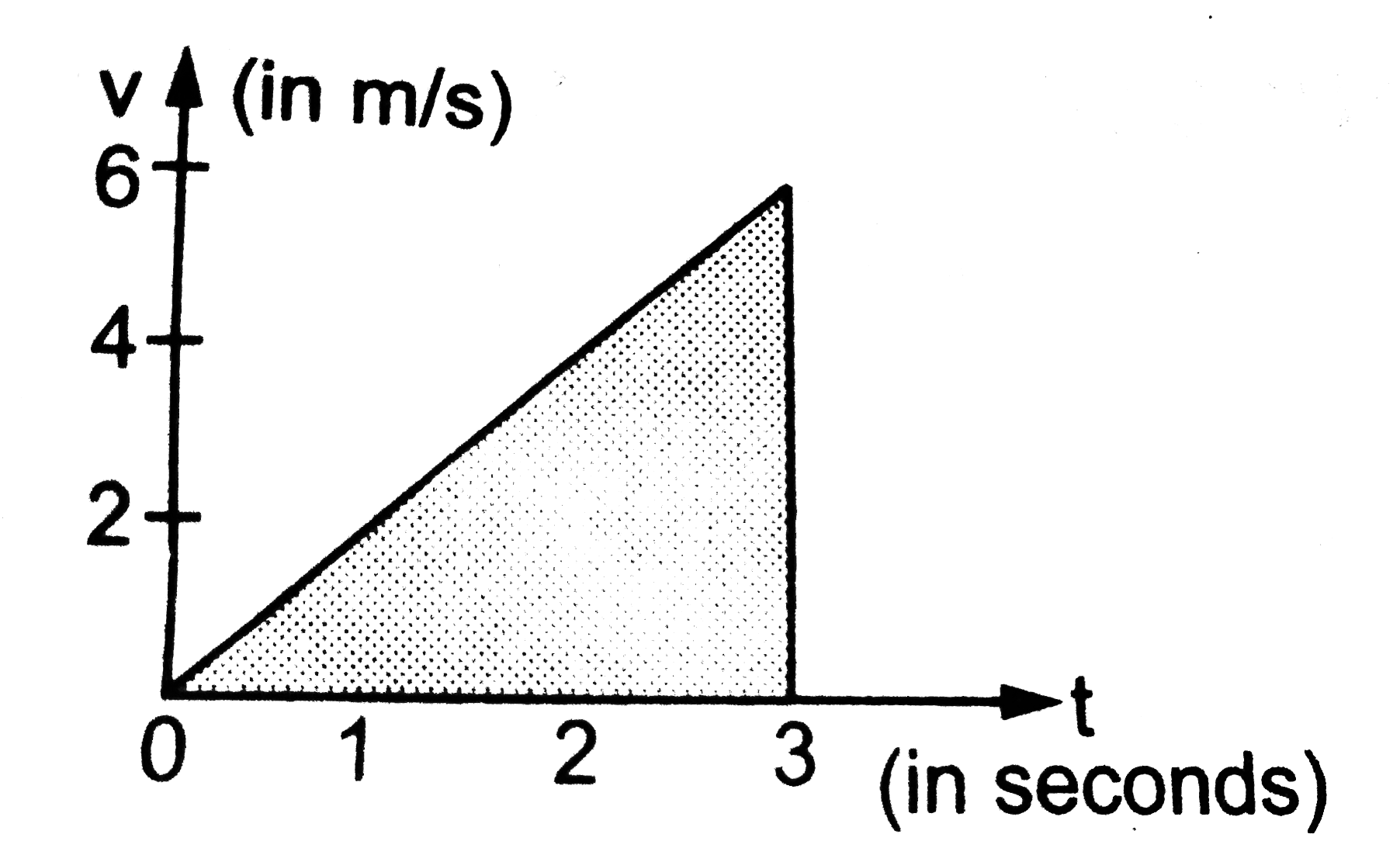 A9mB5mC2mD1m
A9mB5mC2mD1mA point mass of 0.5 kg is moving along x− axis as x=t2+2t , where, x is in meters and t is in seconds. Find the work done (in J) by all the forces acting on the body during the time interval [0,2s].
A6JB7JC8JD9J
The position of a particle moving along a straight line is defined by the relation, x=t3−6t2−15t+40 where x is in meters and t in seconds.The distance travelled by the particle from t=0 to t=2 s is?
View SolutionThe x -coordinate of a particle moving along x -axis varies with time as x=6-4t+t^(2), where x in meter and t in second then distance covered by the particle in first 3 seconds is
View SolutionA particle is moving along x-axis. Its X-coordinate varies with time as, X=2t2+4t−6 Here, X is in meters and t in seconds. Find average velocity between the time interval t=0→t=2s.
View SolutionThe distance travelled (in meters) by the particle from time t = 0 to t = t will be –
View SolutionThe distance travelled (in meters) by the particle from time to t = 0 to t = 1s will be –
View SolutionThe speed verses time graph for a particle is shown in the figure. The distance travelled (in m) by the particle during the time interval t = 0 to t = 5 s will be __________

View Solution

