In a Young's double slit experiment the amplitudes of the two waves incident on the two slits are A and 2A. If I0 is the maximum intensity, then the intensity at a spot on the screen where the phase difference between the two interfering waves is ϕ .
I0cos2(ϕ/2)
I03sin2(ϕ/2)
(I09(5+4cos(ϕ))
I09(5+8cos(ϕ))
The correct Answer is:C
To solve the problem, we need to find the intensity at a point on the screen in a Young's double slit experiment where the amplitudes of the two waves are given as A and 2A, and there is a phase difference ϕ between them.
1. Identify the Amplitudes:
- Let the amplitude of the first wave be A1=A.
- Let the amplitude of the second wave be A2=2A.
2. Calculate the Intensities:
- The intensity of a wave is proportional to the square of its amplitude. Thus, we can calculate the individual intensities:
I1=A21=A2
I2=A22=(2A)2=4A2
3. Find the Resultant Intensity Formula:
- The resultant intensity IR for two waves with phase difference ϕ is given by:
IR=I1+I2+2√I1I2cos(ϕ)
- Substituting the values of I1 and I2:
IR=A2+4A2+2√A2⋅4A2cos(ϕ)
IR=5A2+2⋅2A2cos(ϕ)
IR=5A2+4A2cos(ϕ)
4. Determine the Maximum Intensity I0:
- The maximum intensity I0 occurs when cos(ϕ)=1 (i.e., when ϕ=0):
I0=5A2+4A2⋅1=5A2+4A2=9A2
5. Express the Resultant Intensity in Terms of I0:
- Now, we can express IR in terms of I0:
IR=5A2+4A2cos(ϕ)
- Since I0=9A2, we can write:
IR=59I0+49I0cos(ϕ)
6. Final Expression for Intensity:
- Therefore, the intensity at a point on the screen where the phase difference is ϕ is:
IR=5+4cos(ϕ)9I0
Conclusion:
The intensity at a spot on the screen where the phase difference between the two interfering waves is ϕ is given by:
IR=5+4cos(ϕ)9I0
- Let the amplitude of the first wave be A1=A.
- Let the amplitude of the second wave be A2=2A.
- The intensity of a wave is proportional to the square of its amplitude. Thus, we can calculate the individual intensities:
I1=A21=A2
I2=A22=(2A)2=4A2
- The resultant intensity IR for two waves with phase difference ϕ is given by:
IR=I1+I2+2√I1I2cos(ϕ)
- Substituting the values of I1 and I2:
IR=A2+4A2+2√A2⋅4A2cos(ϕ)
IR=5A2+2⋅2A2cos(ϕ)
IR=5A2+4A2cos(ϕ)
- The maximum intensity I0 occurs when cos(ϕ)=1 (i.e., when ϕ=0):
I0=5A2+4A2⋅1=5A2+4A2=9A2
- Now, we can express IR in terms of I0:
IR=5A2+4A2cos(ϕ)
- Since I0=9A2, we can write:
IR=59I0+49I0cos(ϕ)
- Therefore, the intensity at a point on the screen where the phase difference is ϕ is:
IR=5+4cos(ϕ)9I0
The intensity at a spot on the screen where the phase difference between the two interfering waves is ϕ is given by:
IR=5+4cos(ϕ)9I0
Topper's Solved these Questions
Similar Questions
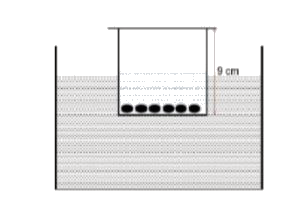
A wide bottom cylindrical massless plastic container of height 9 cm has 40 identical coins inside it and is floating on water with 3 cm inside the water. If we start putting more of such coins on its lid. It is observed that after N coins are put, its equilibrium changes from stable to unstable. Equilibrium in floating is stable if the geometric center of the submerged portion is above the center of mass of the object) The value of N is closed to
View SolutionConsider an YDSE that has different slit width. As a result, amplitude of waves from two slits are A and 2A, respectively. If I_(0) be the maximum intensity of the interference pattern, then intensity of the pattern at a point where phase difference between waves is phi is
View SolutionIn the Young's double slit experiment, if the phase difference between the two waves interfering at a point is ϕ, the intensity at that point can be expressed by the expression
View SolutionIn Young's double slit experiment, if I_(0) is intensity of light from each sources, what is the intensity at a point on screen where two waves arrive having a phase diff. of 60^(@) and 120^(@) .
View SolutionThe maximum intensity in Young's double slit experiment is I0 . What will be the intensity of light in front of one the slits on a screen where path difference is λ4 ?
View SolutionIf the intensities of the two interfering beam in Young's double-slit experiment are I1 and I2, then the constrast between the maximum and minimum intensities are good when
View SolutionIn Young's double slit experiment, phase difference between the waves at a point on screen having intensity less than the average intensity on screen may be
View SolutionThe intensity of each of the two slits in Young's double slit experiment is I_(0) Calculate the minimum separation between the two points on the screen where intensities are 2I_(0) and I_(0) Given the fringe width equal to alpha
View SolutionIn Young's double slit experiment, the maximum intensity is I_(0) . What is the intensity at a point on the screen where the path difference between the interfering waves is lamda/4 ?
View SolutionFind the intensity at a point on a screen in Young's double slit experiment where the interfering waves of equal intensity have a path difference of λ4
View SolutionFind the intensity at a point on a screen in Young's double slit experiment where the interfering waves of equal intensity have a path difference of λ3
View SolutionIn the Young’s double slit experiment, the resultant intensity at a point on the screen is 75% of the maximum intensity of the bright fringe. Then the phase difference between the two interfering rays at that point is
View SolutionIn Young's double-slit experiment, the path difference between two interfering waves at a point on the screen is 13.5 times the wavelength. The point is
View SolutionThe intensity of each of the two slits in Young's double slit experiment is I_(0) Calculate the minimum separation between the two points on the screen where intensities are 2I_(0) and I_(0) Given the fringe width equal to alpha
View SolutionThe maximum intensity in Young's double slit experiment is I_(0) . What will be the intensity of light in front of one the slits on a screen where path difference is (lambda)/(4) ?
View Solution

