In Young's double slit experiment, phase difference between the waves at a point on screen having intensity less than the average intensity on screen may be
π/4
2π/3
π
7π/8
The correct Answer is:B, C, D
Let maximum intensity be I0
I=I0ωtΔϕ2
Iav=I02
I<Iav⇒cos2(Δϕ2)<12
⇒cos(Δϕ2)<1√2
⇒π2<Δϕ<3π2
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective
107 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
In young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
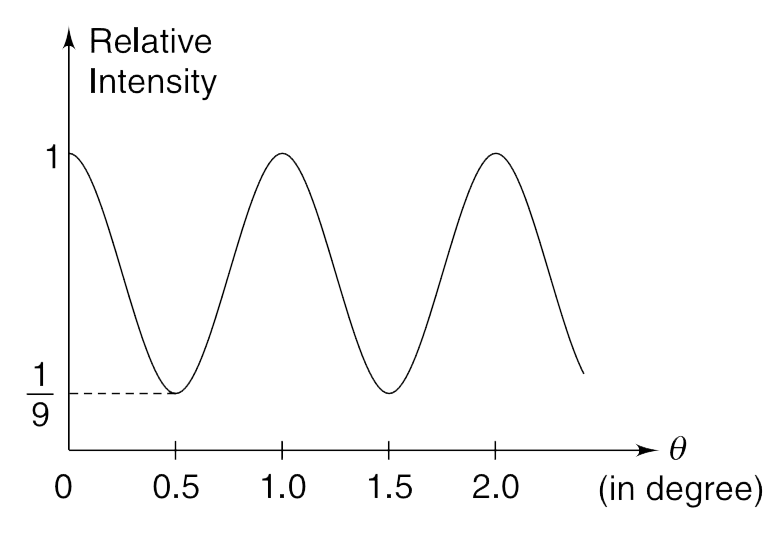
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.
View SolutionIn Young's double-slit experiment, the path difference between two interfering waves at a point on the screen is 5λ2,λ being wavelength of the light used. The ___________ dark fringe will lie at this point.
View Solution
Knowledge Check
In Young's double-slit experiment, the path difference between two interfering waves at a point on the screen is 13.5 times the wavelength. The point is
ABright but not central brightBNeither bright not darkCCentral brightDDarkIn Young's double slit experiment, the phase difference between the two waves reaching at the location of the third dark fringe is
AπB3π2C5πD3πIn the Young's double slit experiment, if the phase difference between the two waves interfering at a point is ϕ, the intensity at that point can be expressed by the expression
A(a) I=√A2+B2cos2φB(b) I=ABcosφC(c)I=A+Bcosφ2D(d) I=A+Bcosφ
In Young's double slit experiment the phase difference between the waves reaching the central fringe and fourth bright fringe will be
View SolutionIn a Young's double slit experiment, the central point on the screen is
View SolutionIntensities of light due to the two slits of Young's double-slit experiment are I and 4I. How far from the centre maxima will the intensity be equal to the average intensity on the screen? (β is the fringe width.)
View SolutionIn Young's double-sit experiment, if the superimposing waves have amplitude a0 and intensity I0, then the average intensity of the light in te fringe pattern formed on a screen will be
View SolutionIn Youngsdoub≤slitexperiment,thephased⇔erentbetweentwocoherentsourcesofequal∫ensityisπ3.The∫ensityatap∮whichisatequaldistanceomthetwoslitsis(l_@) is maximum intensity)
View Solution
