The drawing shows two cylinders. They are identicle in all respects, except one is hollow. In a setup like that in figure identical forces are applied to the right end of each cylinder while the left end is fixed.

The elongation of A is morethan that of B
The elongation of B is morethan that of A
The energy stored in B is more than is A
The energy stored in A is more than that in B
The correct Answer is:B, C
FA=yΔll⇒Δl=(lFr)1A
⇒U=12(Δrl)Δl2=12Δrl(ΔFr)21A2
⇒U∝1A
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Subjective
Explore 107 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Reasoning
Explore 75 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A cylinder of mass m suspended by two strings wrapped around the cylinder one near each end, the free ends of the string being attached to hooks on the ceiling, such that the length of the cylinder is horizontal. From the position of rest , the cylinder is allowed to roll down as suspension strings unwind , calculate
(a) The downward linear acceleration of the cylinder
(b) The tension in the strings
(c) The time dependence of the instantaneous power developed by gravity
View SolutionFigure shows a 300 kg cylinder that is horizontal. Three steel wires support the cylinder from a ceiling. Wires 1 and 3 are attached at the ends of the cylinder, and wire 2 is attached at the center. The wires each have a cross - sectional area of 2.00×10−6m2. Initially (before the cylinder was put in place), wires 1 and 3 were 2.0000 m long and wire 2 was 6.00 mm longer than that. Now (with the cylinder in place), all three wires have been stretched. What is the tension in wire 1 (kN) ? (Esteel=200×109N/m2)

View Solution
Knowledge Check
A horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
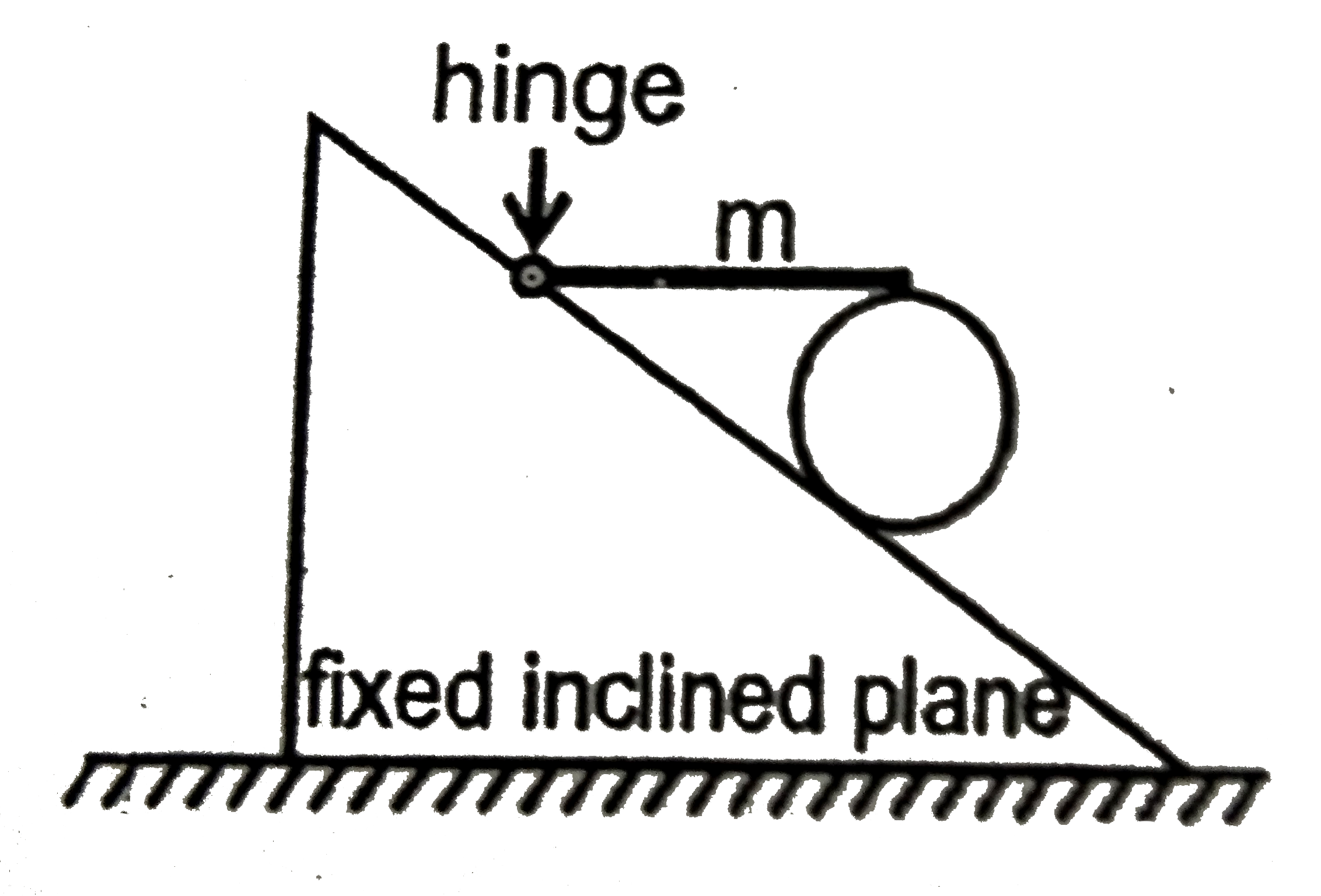
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :A1:1B2:√3C2:1D√2:1A rod not toching the flor is inserted between two identical boxes (see figure) There is a very small gap between the rod and and boxes ,A horizontal force F is applied at the upper end of the rod There is frication between boxes and the floor Assume that the od remains almost vertical after the force is applied which of hte following is /are correct?
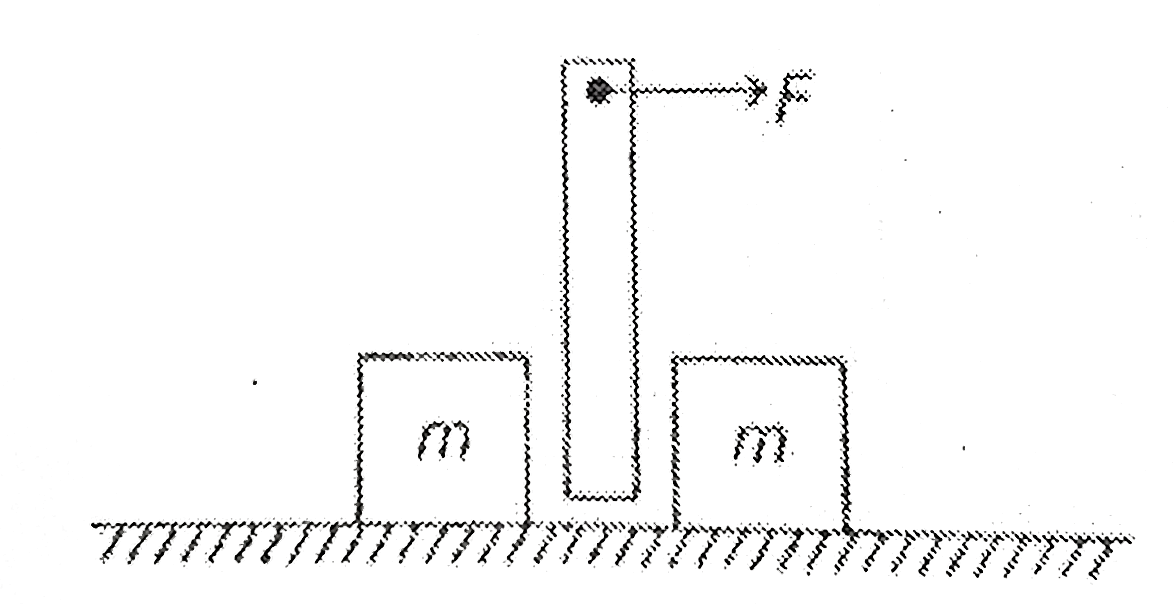 ABoth the boxes will move simultaneouslyBright box will move firstCleft box will move firstDFriction force on right block is more than left block before the block move
ABoth the boxes will move simultaneouslyBright box will move firstCleft box will move firstDFriction force on right block is more than left block before the block moveIn an experiment , setup A consists of two parallel wires which carry currents in opposite directions as shown in the figure. A second setup B is identical to setup A, except that there is a metal plate between the wires

Let FA and FB be the magnitude of the force between the two wires in setup A and setup B, respectively.AFA>FB≠0BFA<FBCFA=FB≠0DFA>FB=0
A uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA metal cylinder of radius R is placed on a wooden plank BD. The plank is kept horizontal suspended with the help of two identical string AB and CD each of length L. The temperature coefficient of linear expansion of the cylinder and the strings are a1 and a2 respectively. Angle q shown in the figure is 30∘. It was found that with change in temperature the centre of the cylinder did not move. Find the ratio α1α2 , if it is know that L = 4R. Assume that change in value of θ is negligible for small temperature changes

View SolutionTwo metallic cylinder made of same material and radii r and 2r are joined as shown in figure. If top end is ved and lower end of cylinder B is twisted by angle e, then angle of twist for cylinder A is (both cylinder have fixed and

View SolutionCONE + CYLINDER + HEMISPHERE : A toy is in the shape of a right circular cylinder with a hemisphere on one end and a come on the other. The height and radius of the cylinderical part are 13cm and 5cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylinderical part. Calculate the surface area of the toy if height of the conical part is 12 cm.
View SolutionOne end of meter stick is pinned to a table to that stick can rotate freely in aplane parallel to the table surface. Two horizontal forces are applied to the stick such that the rod does not rotate at all. One force has a magnitude of 2N and is applied perpendicular to the stick at the free end. The other force has a magnitude of 8N and acts at 30∘ with respect in the length of the stick. At what distance from the pinned end is the 8N force applied.
View Solution