A point object is kept at (1,0,0). A circular plane mirror of radius 1m is kept in yz-plane such that its centre is at the origin. The reflecting side faces positive x-axis At which of the following points can the image of the object be seen?
(-0.5,0,0.5)
(2,2,2)
(1,1.5,1.5)
(1,-1,1.5)
The correct Answer is:B, D
To solve the problem of determining at which points the image of the object can be seen, we follow these steps:
Step 1: Understand the setup
- The point object is located at (1, 0, 0).
- The circular plane mirror is in the yz-plane, centered at the origin (0, 0, 0), with a radius of 1 meter.
- The reflecting side of the mirror faces the positive x-axis.
Step 2: Determine the image position
- The image of the object in a plane mirror is located at an equal distance behind the mirror. Since the object is at (1, 0, 0), the image will be at (-1, 0, 0).
Step 3: Determine the field of view
- The field of view from the mirror can be visualized as a cone with its vertex at the image point (-1, 0, 0) and opening towards the positive x-axis.
- The radius of the mirror is 1 meter, and the distance from the mirror to the object is 1 meter. Therefore, the cone will have a height of 1 meter and a base radius of 1 meter.
Step 4: Calculate the cone's dimensions
- The cone's angle can be determined using the relationship of the radius and height. The angle θ can be calculated using:
tan(θ)=radiusheight=11=1⟹θ=45∘
- The cone will extend from the image point (-1, 0, 0) and can be described mathematically.
Step 5: Identify the points given in the options
We will analyze each option to see if it lies within the field of view of the cone.
1. Option A: (-0.5, 0, 0.5)
- This point is behind the mirror (x < 0), hence it cannot see the image.
2. Option B: (2, 2, 2)
- This point is at x = 2. The distance from the image (-1, 0, 0) to this point can be calculated:
Distance=√(2−(−1))2+(2−0)2+(2−0)2=√(3)2+(2)2+(2)2=√9+4+4=√17
- The radius of the cone at x = 2 is 3 (since the cone opens outwards), so this point can see the image.
3. Option C: (1, 1.5, 1.5)
- This point is at x = 1. The distance from the image (-1, 0, 0) to this point is:
Distance=√(1−(−1))2+(1.5−0)2+(1.5−0)2=√(2)2+(1.5)2+(1.5)2=√4+2.25+2.25=√8.5
- The radius of the cone at x = 1 is 2, which is less than the distance calculated. Thus, this point cannot see the image.
4. Option D: (1, -1, 1.5)
- This point is also at x = 1. The distance from the image (-1, 0, 0) is:
Distance=√(1−(−1))2+(−1−0)2+(1.5−0)2=√(2)2+(−1)2+(1.5)2=√4+1+2.25=√7.25
- The radius of the cone at x = 1 is still 2, which is greater than the distance calculated. Thus, this point can see the image.
Conclusion
The points where the image can be seen are:
- Option B: (2, 2, 2)
- Option D: (1, -1, 1.5)
- The point object is located at (1, 0, 0).
- The circular plane mirror is in the yz-plane, centered at the origin (0, 0, 0), with a radius of 1 meter.
- The reflecting side of the mirror faces the positive x-axis.
- The image of the object in a plane mirror is located at an equal distance behind the mirror. Since the object is at (1, 0, 0), the image will be at (-1, 0, 0).
- The field of view from the mirror can be visualized as a cone with its vertex at the image point (-1, 0, 0) and opening towards the positive x-axis.
- The radius of the mirror is 1 meter, and the distance from the mirror to the object is 1 meter. Therefore, the cone will have a height of 1 meter and a base radius of 1 meter.
- The cone's angle can be determined using the relationship of the radius and height. The angle θ can be calculated using:
tan(θ)=radiusheight=11=1⟹θ=45∘
- The cone will extend from the image point (-1, 0, 0) and can be described mathematically.
We will analyze each option to see if it lies within the field of view of the cone.
- This point is behind the mirror (x < 0), hence it cannot see the image.
- This point is at x = 2. The distance from the image (-1, 0, 0) to this point can be calculated:
Distance=√(2−(−1))2+(2−0)2+(2−0)2=√(3)2+(2)2+(2)2=√9+4+4=√17
- The radius of the cone at x = 2 is 3 (since the cone opens outwards), so this point can see the image.
- This point is at x = 1. The distance from the image (-1, 0, 0) to this point is:
Distance=√(1−(−1))2+(1.5−0)2+(1.5−0)2=√(2)2+(1.5)2+(1.5)2=√4+2.25+2.25=√8.5
- The radius of the cone at x = 1 is 2, which is less than the distance calculated. Thus, this point cannot see the image.
- This point is also at x = 1. The distance from the image (-1, 0, 0) is:
Distance=√(1−(−1))2+(−1−0)2+(1.5−0)2=√(2)2+(−1)2+(1.5)2=√4+1+2.25=√7.25
- The radius of the cone at x = 1 is still 2, which is greater than the distance calculated. Thus, this point can see the image.
The points where the image can be seen are:
- Option B: (2, 2, 2)
- Option D: (1, -1, 1.5)
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective107videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A point object is placed at (0, 0, 0) and a plane mirror is placed parallel to YZ plane at x = 2. Find the coordinate of image
View SolutionA circular coil with 100 turns and radius 20 cm is kept in Y-Z plane with its centre at the origin. Find the magnetic field at point (20 cm, 0, 0) if coil carries a current of2.0 A.
View Solution
Knowledge Check
- Question 1 - Select One
A point object of mass m is kept at (a, 0) along x-axis. What mass should be kept at (-3a,0), so that centre of mass lies at origin ?
AmB2mCm3D3m - Question 2 - Select One
A circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
Aλ3√3ε0RB2λ3√3ε0R2C23√3λε0RDnone the these - Question 3 - Select One
The mirror image of the point (1, 2, 3) in a plane is (-1,2,-3) . Which of the following points lies on this plane?
A(0, 1, 2)B(0, 2, 0)C(0, 2, 1)D(1, -1, 1)
A disc is kept on xy plane with centre at origin. Find electric field at a point with distance Z from origin on z-axis.
View SolutionA circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionThe position of the centre of mass of a uniform semi-circular wire of radius 'R' placed in x-y plane with its centre at the origin and the line joining itsends as x-axis is given by (0,xRπ). Then the value of |x| is ______.
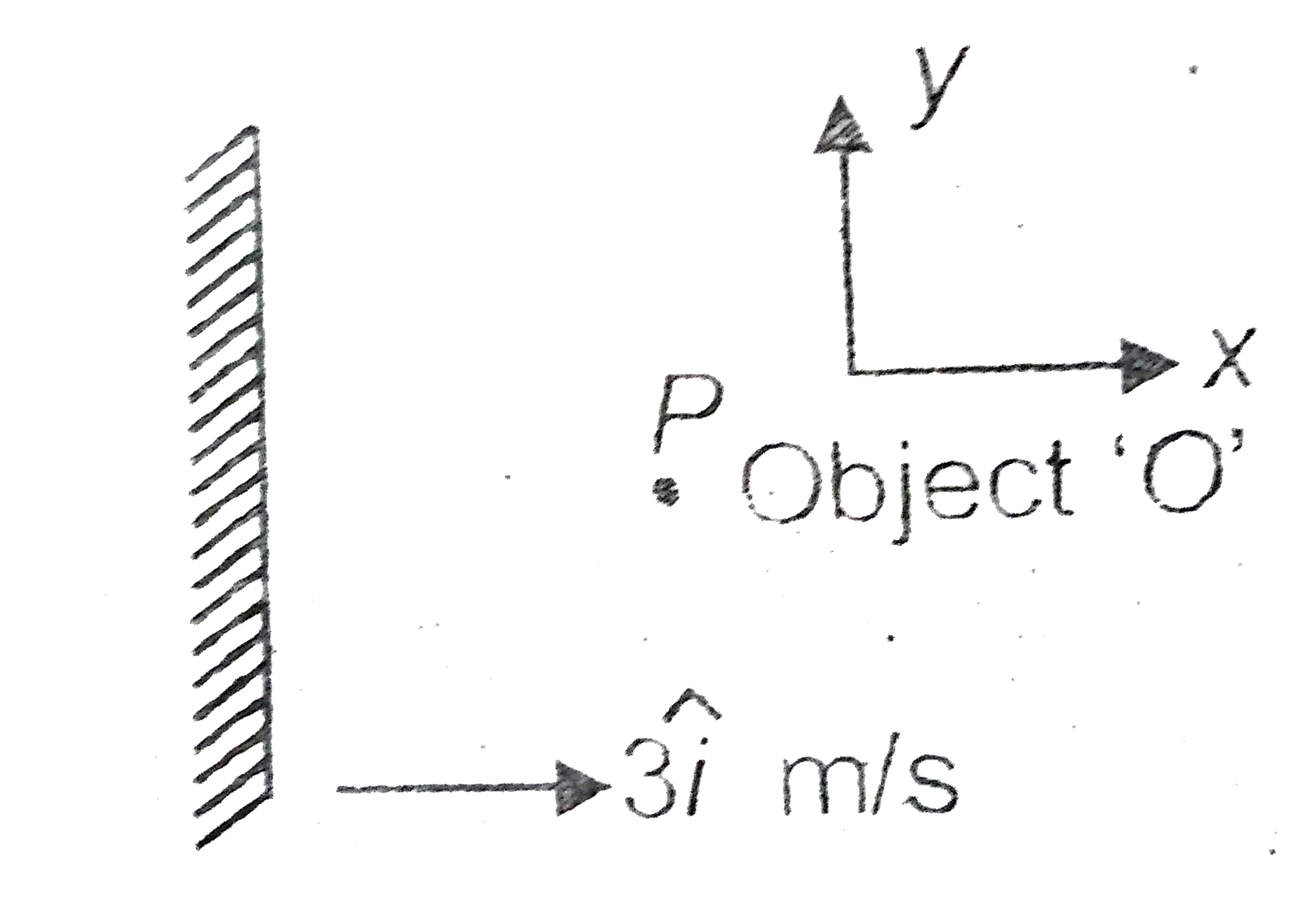
View SolutionFigure shows an object O kept at P. A plane mirror parallel to yz plane is moving with velocity 3ˆim/s. Select the correct alternative
 View Solution
View SolutionAn object is placed 1.5m from a plane mirror. How far is the image from the object?
View Solution

