A wheel of radius R is trapped in a mud pit and spinning. As the wheel is spinning , it splashes mud blobs with initial speed u from various points on its circumference . the maximum height from the center of the wheel , to which mud blob can reach is
u2/2g
u22g+gR22u2
u22g
R+u22g
The correct Answer is:B
Step by step video, text & image solution for A wheel of radius R is trapped in a mud pit and spinning. As the wheel is spinning , it splashes mud blobs with initial speed u from various points on its circumference . the maximum height from the center of the wheel , to which mud blob can reach is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Completion type Question : A body is thrown vertically up from the ground with a speed u and it reaches its maximum height h at time t=t0. The height to which it would have risen at t = (t_0)/2 is………
View SolutionA thin, spherical, conducting shell of radius R is mounted on an isolating support and charged to a potential of-170 V. An electron is then fired directly toward the center of the shell, from point P at distance r from the center of the shell (r>>R). What initial speed v0 is needed for the electron to just reach the shell before reversing direction?
View Solution
Knowledge Check
A cord is wound round the circumference of a wheel of radius r. The axis of the wheel is horizontal and its moment of inertia about this axis is I. A weight mg is attached to the end of the cord and is allowed to fall from rest. The angular velocity of the wheel, when the weight has fallen through a distance h, is
A[2ghl+mr]1/2B[2mghI+mr2]1/2C[2mgh1+2mr2]1/2D(2gh)1/2The original Ferris wheel has a radius of 38 m and completed a full revolution (2π rad) every two minutes when operating at its maximum speed. If the wheel were uniformly slowed from its maximum speed to a stop in 35 s, what would be the magnitude of the tangential acceleration at the outer rim of the wheel during its deceleration?
A0.0015m/s2B0.54m/s2C0.057m/s2D1.6 m/sA projectile is launched from the surface of the earth with a very high speed u at an angle θ with vertical . What is its velocity when it is at the farthest distance from the earth surface . Given that the maximum height reached when it is launched vertically from the earth with a velocity v = √GMR
Aucosθ2Businθ2C√GM2RD√GM3R
A boy ‘A’ is running on a circular track of radius R. His friend, standing at a point O on the circumference of the track is throwing balls at speed u=√gR. Balls are being thrown randomly in all possible directions. Find the length of the circumference of the circle on which the boy is completely safe from being hit by a ball.

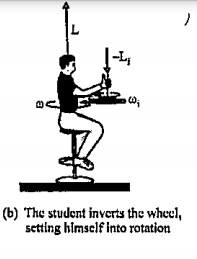
View SolutionFigure shows a student, sitting on a stool that can rotate freely about a vertical axis. The student, initially at rest, is holding a bicycle wheel whose rim is loaded with lead and whose moment of inertia is I about its central axis. The wheel is rotating at an angular speed ωi from an overead perspective, the rotation is counter clockwise. The axis of the wheel point vertical, and the angular momentum →Li of the wheel points vertically upward. The student now inverts the wheel, as a result, the student and stool rotate about the stool axis. With what angular speed and direction does the student then rotate? (The moment of inertia of the student+stool+wheel system about the stool axis is I0)

View SolutionTwo thin rings of slightly different radii are joined together to make a wheel (see figure) of radius R. There is a very small smooth gap between the two ring. The wheel has a mass M and its centre of mass is at its geometrical centre. The wheel stands on a smooth surface and a small particle of mass m lies at the top (A) in the gap between the rings. The system is released and the particle begins to slide down along the gap. Assume that the ring does not lose contact with the surface.

(a) As the particle slides down from top point A to the bottom point B, in which direction does the centre of the wheel move?
(b) Find the speed of centre of the wheel when the particle just reaches the bottom point B. How much force the particle is exerting on the wheel at this instant?
(c) Find the speed of the centre of the wheel at the moment the position vector of the particle with respect to the centre of the wheel makes an angle q with the vertical. Do this calculation assuming that the particle is in contact with the inner ring at desired value of θ
View SolutionA tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.
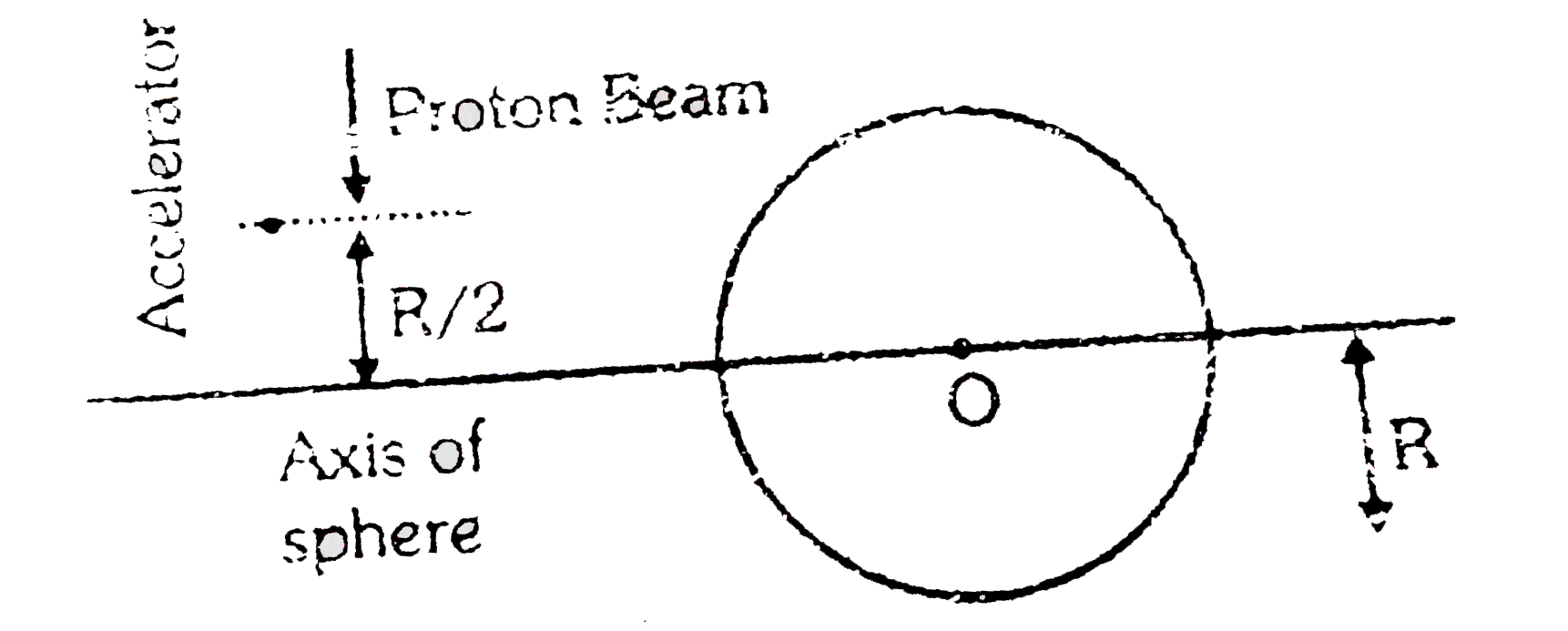
The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
One the potential of the sphere has reached its final, constant value, the minimum speed v of a proton along its trajectory path is given by
View Solution

