The image of an object O due to reflection from the surface of a lake is elongated due to the ripples on the water surface caused by a light breeze. This is because the ripples act as tilted mirrors as shown. Consider the case where O and the observer E are at the same height above the surface of the lake. If the maximum angle that the ripples make with the horizontal is a, the angular extent δ of the image will be

α2
α
2α
4α
The correct Answer is:C
Step by step video, text & image solution for The image of an object O due to reflection from the surface of a lake is elongated due to the ripples on the water surface caused by a light breeze. This is because the ripples act as tilted mirrors as shown. Consider the case where O and the observer E are at the same height above the surface of the lake. If the maximum angle that the ripples make with the horizontal is a, the angular extent delta of the image will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The angle of elevation of a cloud from a height h above the level of water in a lake is α and the angle of depressionof its image in the lake is β. Find the height of the cloud above the surface of the lake:
AhcotβBh(cotα+cotβ)ChcotαDh(cotα+cotβcotα−cotβ)The angle of elevation of a cloud from a height h above the level of water in a lake is α and the angle of depressionof its image in the lake is β. Find the height of the cloud above the surface of the lake:
Ahsin(β−α)sin(α+β)BhsinαChsin(α+β)sin(β−α)Dnone of theseA fish is a little away below the surface of a lake. If the critical angle is 49∘ , then the fish could see things above the water surface with in an angular range of θ∘ where
 Aθ=49∘Bθ=90∘Cθ=90∘Dθ=241∘2
Aθ=49∘Bθ=90∘Cθ=90∘Dθ=241∘2
Surface of the lake is at 2”∘C. The temperature of the bottom of the lake is
View SolutionAnswer true or false
If a pebble is thrown into the water the ripples on the surface of water are created due to translatory motion of the water particles.
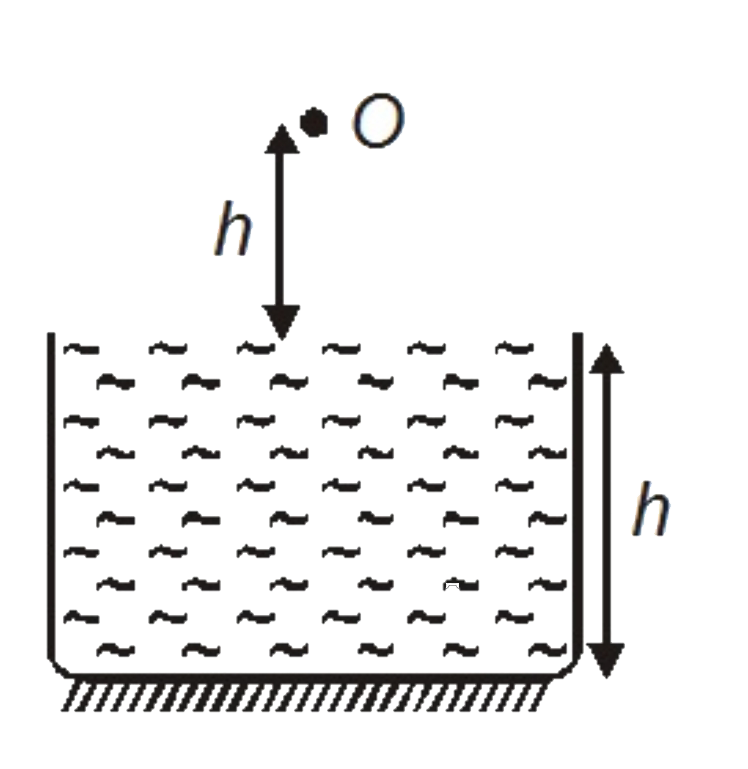
View SolutionAn object O is placed at a height h = 12 cm above water (μ=43) surface in a beaker . The lower surface of the beaker is polished , as shown in the figure . The location of final image will be
View SolutionWay do marine animals live deep inside o lake when the surface of the lake freezes?
View SolutionAn object is projected vertically upward from the surface of the earth at which above and below the surface acceleration due to gravity is the same.
View Solution

