The graph of the equation above is a parabola in the xy-plane. If k>0, what is the minimum value of y expressed in terms of k?
−7k
−16k
−25k
−73k
The correct Answer is:C
To find the minimum value of y expressed in terms of k for the given parabola y=k(x−1)(x+9) where k>0, we can follow these steps:
Step 1: Expand the equation
First, we need to expand the equation to standard form.
y=k(x−1)(x+9)
Expanding this, we have:
y=k(x2+9x−x−9)=k(x2+8x−9)
Step 2: Rewrite in standard form
Next, we want to rewrite the quadratic in the standard form y=a(x−h)2+k to find the vertex.
y=k(x2+8x−9)
We can complete the square for the quadratic expression x2+8x:
1. Take half of the coefficient of x (which is 8), square it, and add and subtract it inside the equation.
2. Half of 8 is 4, and squaring it gives 16.
So, we rewrite:
x2+8x=(x2+8x+16)−16=(x+4)2−16
Substituting this back into the equation gives:
y=k((x+4)2−16−9)=k((x+4)2−25)
Step 3: Final form
Now, we can express y in the standard form:
y=k((x+4)2−25)=k(x+4)2−25k
Step 4: Identify the vertex
From the standard form y=a(x−h)2+k, we can see that the vertex of the parabola is at (−4,−25k).
Step 5: Minimum value of y
Since k>0, the parabola opens upwards, and the minimum value of y occurs at the vertex. Thus, the minimum value of y is:
Minimum value of y=−25k
Final Answer
The minimum value of y expressed in terms of k is:
−25k
First, we need to expand the equation to standard form.
Next, we want to rewrite the quadratic in the standard form y=a(x−h)2+k to find the vertex.
2. Half of 8 is 4, and squaring it gives 16.
Now, we can express y in the standard form:
From the standard form y=a(x−h)2+k, we can see that the vertex of the parabola is at (−4,−25k).
Since k>0, the parabola opens upwards, and the minimum value of y occurs at the vertex. Thus, the minimum value of y is:
The minimum value of y expressed in terms of k is:
Topper's Solved these Questions
- PASSPORT TO ADVANCED MATHBook:ENGLISH SATChapter:PASSPORT TO ADVANCED MATHExercise:Grib-In
Explore 29 Videos
- PASSPORT TO ADVANCED MATHBook:ENGLISH SATChapter:PASSPORT TO ADVANCED MATHExercise:EXERCISE
Explore 80 Videos
- PASSPORT TO ADVANCED MATHBook:ENGLISH SATChapter:PASSPORT TO ADVANCED MATHExercise:EXERCISE
Explore 80 Videos
- PARAMETRIC EQUATIONS Book:ENGLISH SATChapter:PARAMETRIC EQUATIONS Exercise:EXERCISES
Explore 3 Videos
- PIECEWISE FUNCTIONSBook:ENGLISH SATChapter:PIECEWISE FUNCTIONSExercise:EXERCISES
Explore 8 Videos
Similar Questions
Knowledge Check
y=2x2−12x+11
The graph of the equation above is a parabola in the xy-plane. What is the distance between the vertex of the parabola and the point (3, 1)?A1B8C10D12x+7y=−10
3x−4y=k
In the system of equation above,k is a constant. IF (a,b) is the solution to the system, what is the value of a, in terms of k?A−k−3025B3k+1025C6k−825D7k−4025y=x2+3
y=15x−33
The system of equations shown above is graphed in the xy-plane. IF system has two solutions, what is the product of the x-coordinates of the two solutions?A36B4C-4D-36
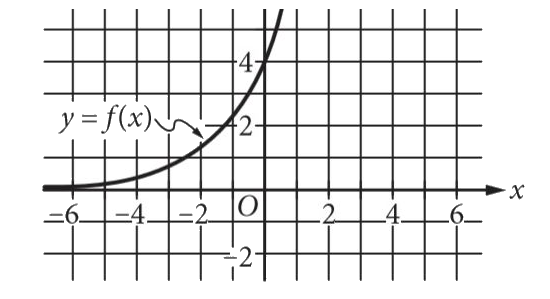
The graph of y = f (x) is shown in the xy -plane. What is the value of f (0) ?
View Solution2.4x − 1.5y = 0.3
1.6x + 0.5y = −1.3
The system of equations above is graphed in the xy -plane. What is the x -coordinate of the intersection point (x , y) of the system?
View SolutionIf the equation above is true, then what is the positive value of the expression 10√x−15 ?
View Solution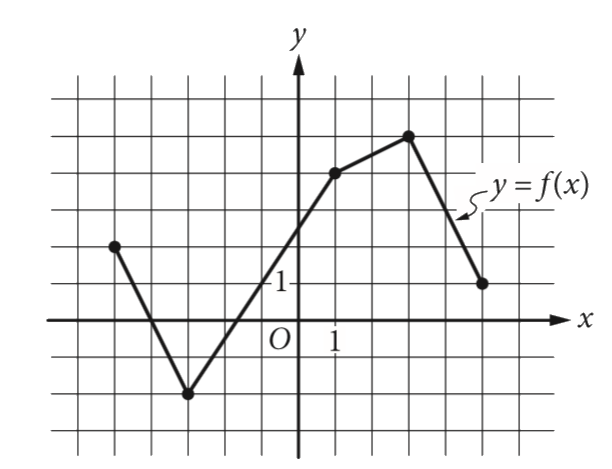
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?
View SolutionThe graph of y+3=(x−4)2−6 is a parabola in the xy-plane. What are the x-intercepts of the parabola?
View Solution


