f(x)=ax2+bx+c,a>0
The coordinates of the lowest point on the graph of the function defined by the equation above is (3,2). If f(−1)=p, then which of the following represents the value of p?
f(−5)
f(−4)
f(6)
f(7)
The correct Answer is:D
To solve the problem, we need to find the value of p where p=f(−1) for the quadratic function f(x)=ax2+bx+c with the vertex (lowest point) at the coordinates (3,2).
1. Identify the vertex form of the quadratic function:
Since the vertex of the parabola is given as (3,2), we can express the function in vertex form:
f(x)=a(x−3)2+2
Here, a>0 ensures that the parabola opens upwards.
2. Calculate f(−1):
We need to find f(−1):
f(−1)=a(−1−3)2+2
Simplifying this:
f(−1)=a(−4)2+2=16a+2
3. Use symmetry of the parabola:
The vertex (3,2) implies that the parabola is symmetric about the line x=3. Therefore, the point (−1,f(−1)) is symmetric to the point (7,f(7)) across the line x=3. Thus, we have:
f(−1)=f(7)
4. Calculate f(7):
Now, we can also find f(7):
f(7)=a(7−3)2+2
Simplifying this:
f(7)=a(4)2+2=16a+2
5. Conclusion:
Since f(−1)=f(7), we have:
p=f(−1)=16a+2
Final Answer:
The value of p can be represented as:
p=16a+2
Since the vertex of the parabola is given as (3,2), we can express the function in vertex form:
f(x)=a(x−3)2+2
Here, a>0 ensures that the parabola opens upwards.
We need to find f(−1):
f(−1)=a(−1−3)2+2
Simplifying this:
f(−1)=a(−4)2+2=16a+2
The vertex (3,2) implies that the parabola is symmetric about the line x=3. Therefore, the point (−1,f(−1)) is symmetric to the point (7,f(7)) across the line x=3. Thus, we have:
f(−1)=f(7)
Now, we can also find f(7):
f(7)=a(7−3)2+2
Simplifying this:
f(7)=a(4)2+2=16a+2
Since f(−1)=f(7), we have:
p=f(−1)=16a+2
The value of p can be represented as:
p=16a+2
Topper's Solved these Questions
- PASSPORT TO ADVANCED MATHBook:ENGLISH SATChapter:PASSPORT TO ADVANCED MATHExercise:Grib-In
Explore 29 Videos
- PASSPORT TO ADVANCED MATHBook:ENGLISH SATChapter:PASSPORT TO ADVANCED MATHExercise:EXERCISE
Explore 80 Videos
- PASSPORT TO ADVANCED MATHBook:ENGLISH SATChapter:PASSPORT TO ADVANCED MATHExercise:EXERCISE
Explore 80 Videos
- PARAMETRIC EQUATIONS Book:ENGLISH SATChapter:PARAMETRIC EQUATIONS Exercise:EXERCISES
Explore 3 Videos
- PIECEWISE FUNCTIONSBook:ENGLISH SATChapter:PIECEWISE FUNCTIONSExercise:EXERCISES
Explore 8 Videos
Similar Questions
Knowledge Check
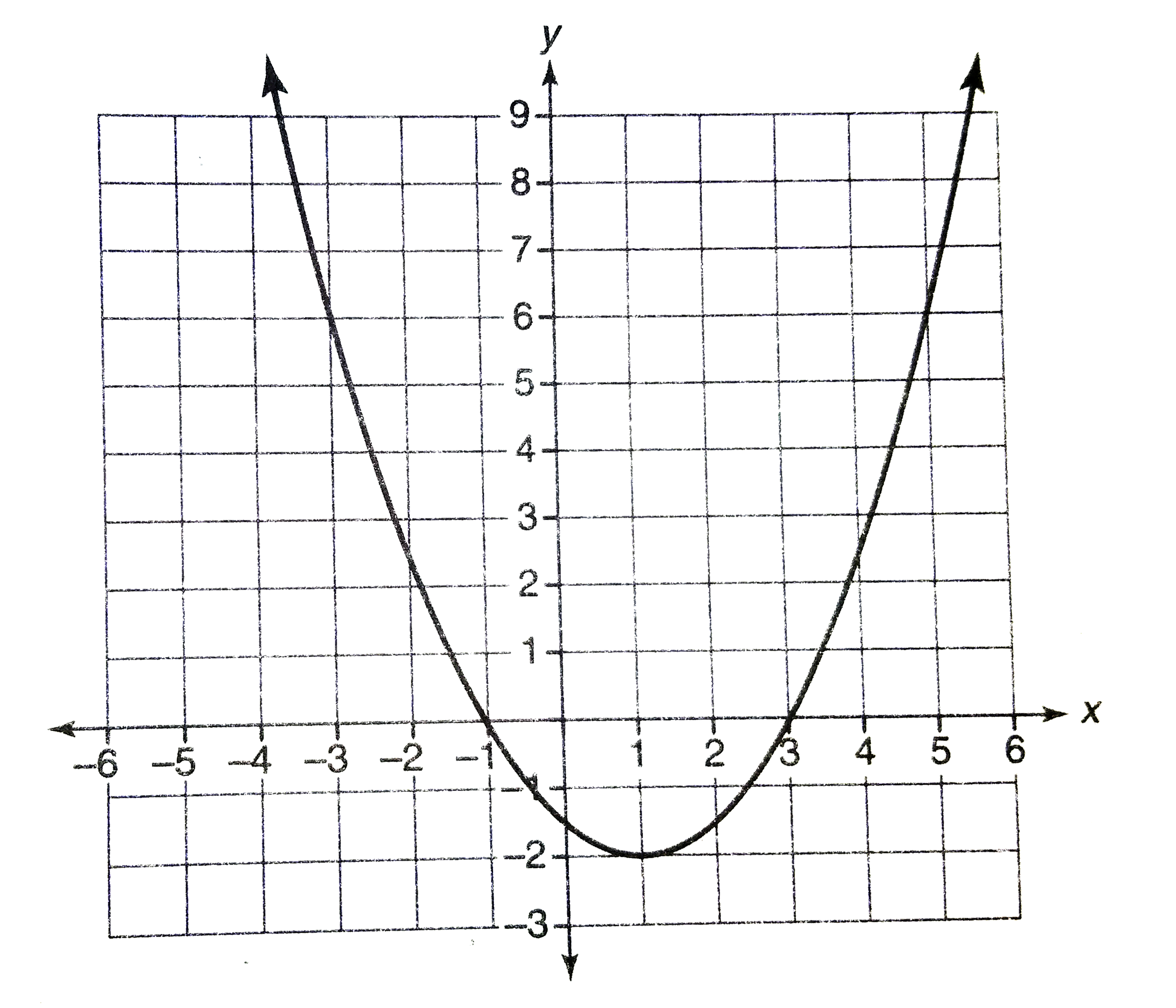
The figure above shows the graph of the quadratic function f with a minimum point at (1,−2). If f(5)=f(c), then which of the following could be the values of c?A−5B−3C0D6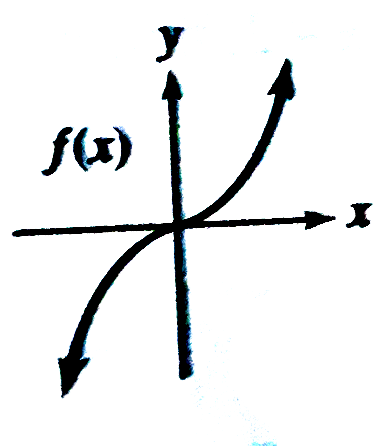
The graph of f(x) is shown above , Which of the following represents the graph of f(x-3) ?A B
B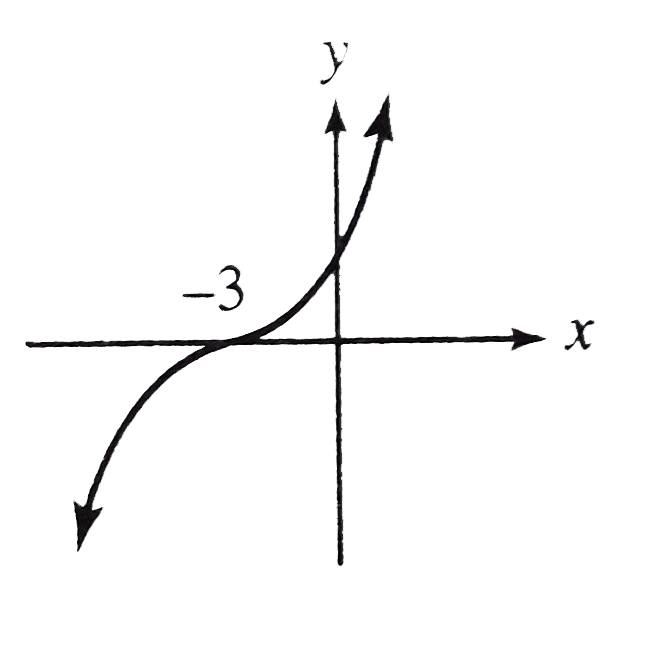 C
C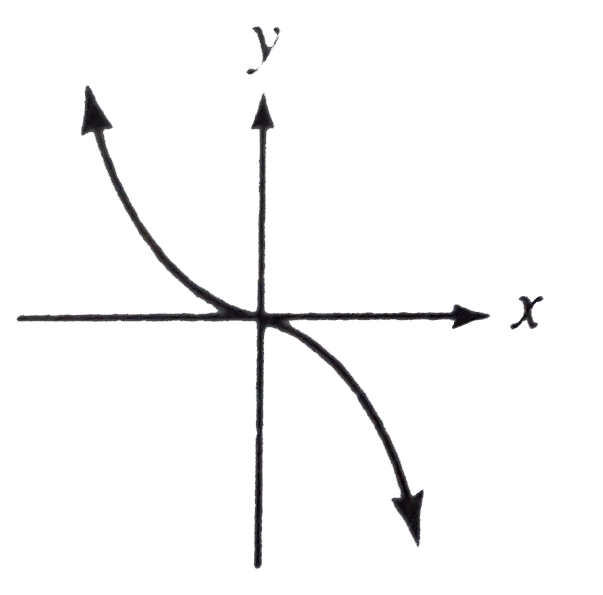 D
D
Function f is defined by the equation f(x)=ax2+2ax. If f(3)−f(2)=1, what is the smallest possible value of a?
A16B15C12D12
f(x)=(2−3x)(x+3)+4(x2−6)
What is the sum of the zeros of function f defined by the equation above?
View Solution
If the accomanying figure above shows the graph of function f, which of the following could represent the graph of y=f(x+1)?
View Solution
The quadratic y=f(x) is shown above. Which of the following graphs represents the function y=f(x+3)−4?
View Solution
The graph of the function f is shown above. Which of the following could represent the graph of y=|f(x)|?
View Solution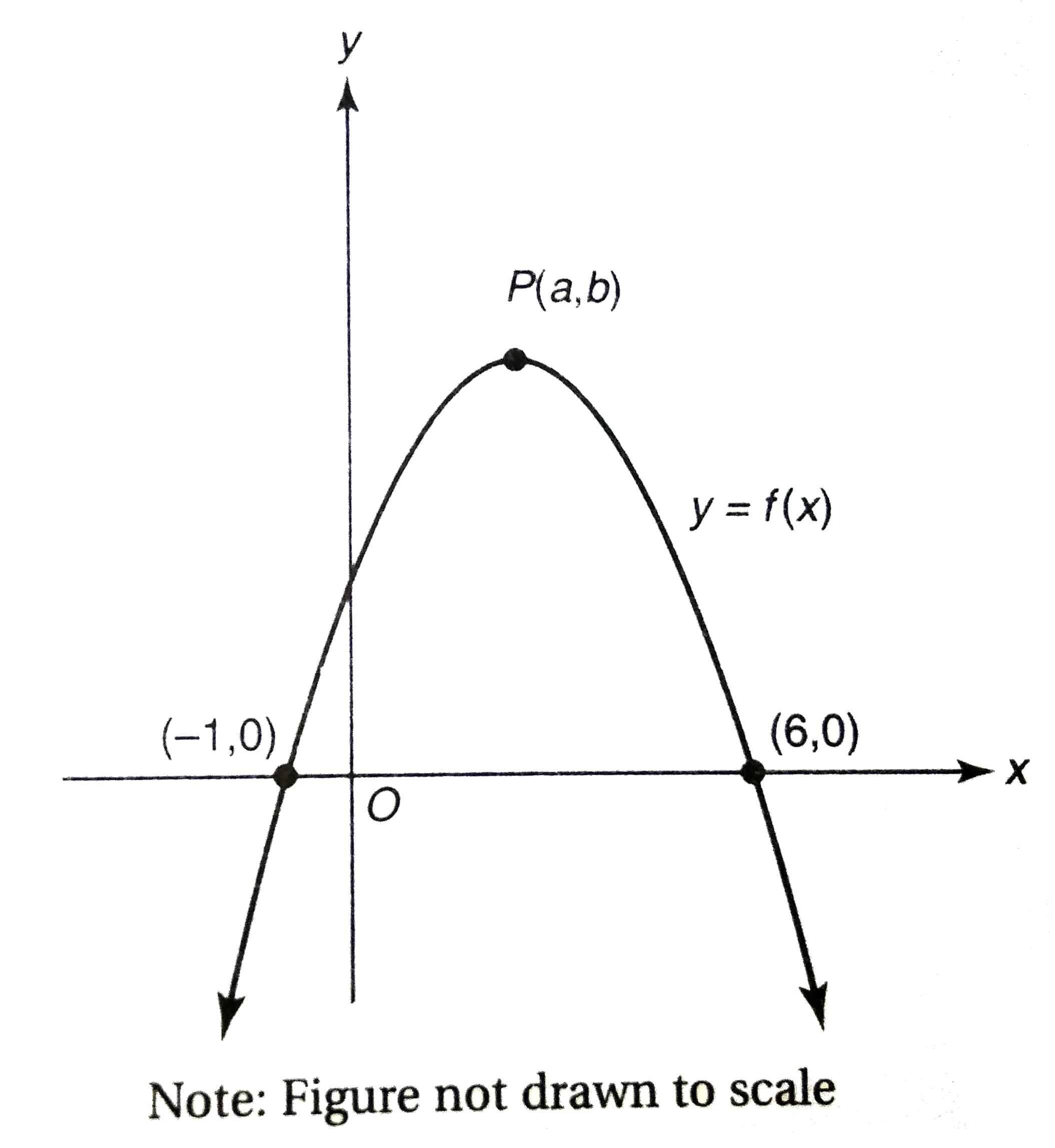
The graph of a quadratic function f is shown in the above figure. If f(x)≤b for all values of x, which of the following could be the coordinates of point P?
View Solution

