A ball of radius R and mass m is rolling without slipping on a horizontal surface with velocity of its centre of mass vCM. It then rolls wilthout slippig up a hill to a height h before momentarily coming to rest. Find h
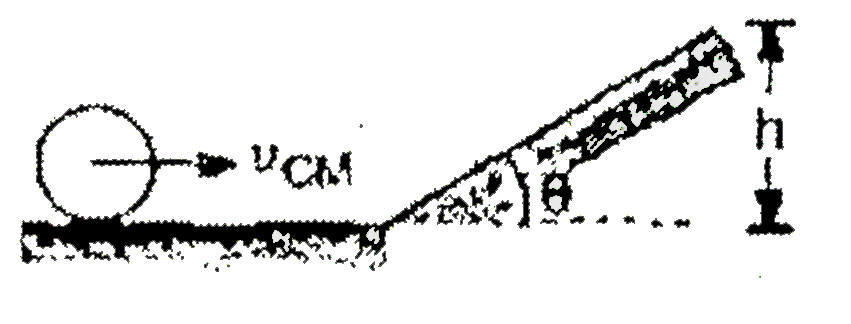
Step by step video & image solution for A ball of radius R and mass m is rolling without slipping on a horizontal surface with velocity of its centre of mass v_(CM). It then rolls wilthout slippig up a hill to a height h before momentarily coming to rest. Find h by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE
83 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE
41 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
A disc of mass 100 g is rolling without slipping on a horizontal surface with a velocity of 10cms−1. Calculate its total energy.
View SolutionA spherical ball of radius r and mass m is rolling without slipping on a horizontal table. Calculate the percentage of KE, which is translational.
View Solution
Knowledge Check
A wheel of bicycle is rolling without slipping on a level road. The velocity of the centre of mass is vCM, then true statement is
 AThe velocity of point A is 2vCM and velocity of point B is zeroBThe velocity of point A is zero and velocity of point B is 2vCMCThe velocity of point A is 2vCM and velocity of point B is −vCMDThe velocities of both A and V are vCM
AThe velocity of point A is 2vCM and velocity of point B is zeroBThe velocity of point A is zero and velocity of point B is 2vCMCThe velocity of point A is 2vCM and velocity of point B is −vCMDThe velocities of both A and V are vCMA wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
AzeroBvC2vD√2vA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)
A disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.
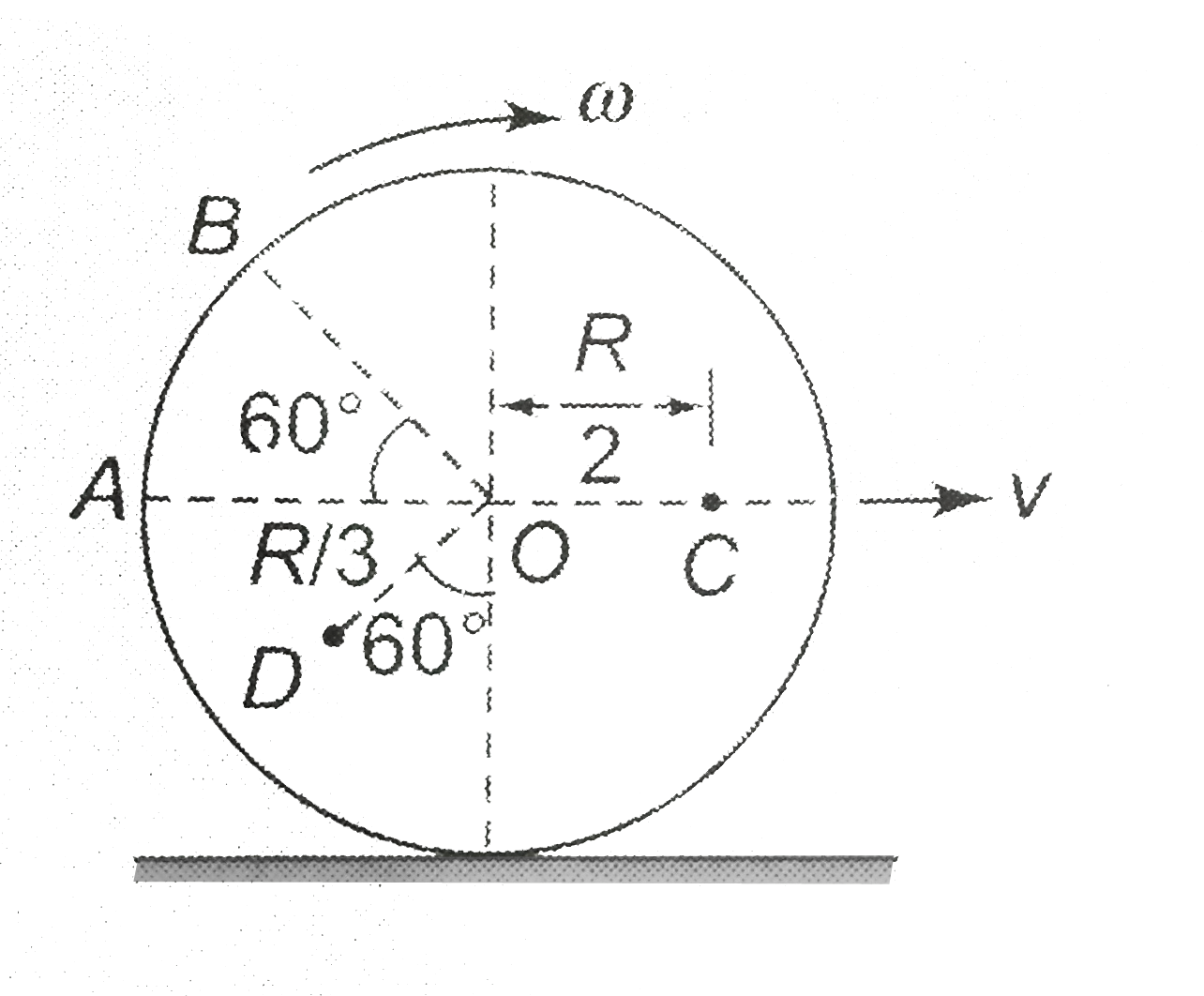
View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass
View Solution
A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration at
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionA solid sphere of mass m= 500gm is rolling without slipping on a horizontal surface. Find kinetic energy of a sphere if velocity of centre of mass is 5 cm/sec
View Solution
