A disc rolls without slipping on a horizontal surface such that its velocity of center of the mass is v. Find the velocity of points A,B,C and D.
If a body rolls without slipping, the velocity of a point of a body is resultant of two velocities, one due to translation of body and another due to rotation of body about its center of mass.
Point A :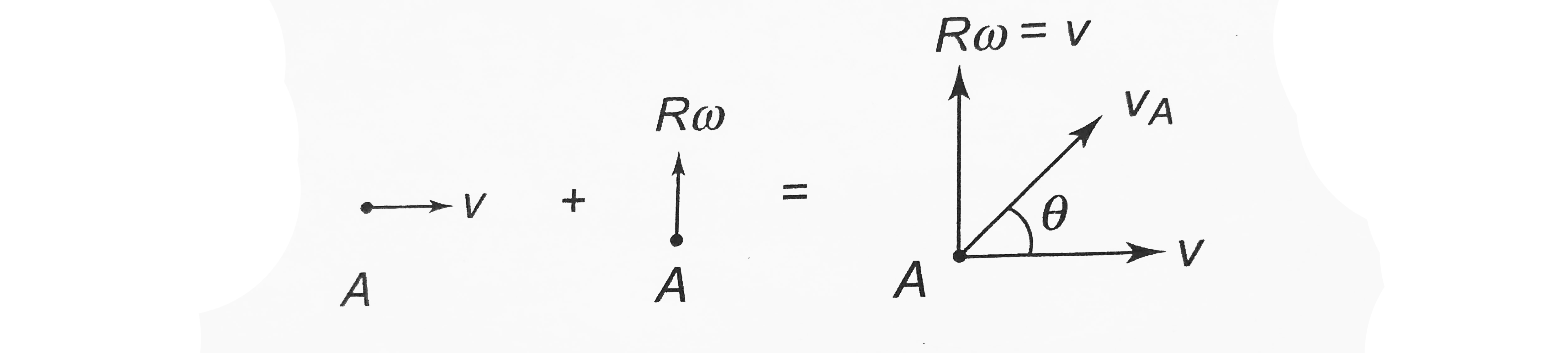 
vA=√2v,θ=45∘
Point B : 
vB=√v2+v2+2v×vcosθ30∘
=√2v2+√3v2=y√2+√3
Point C :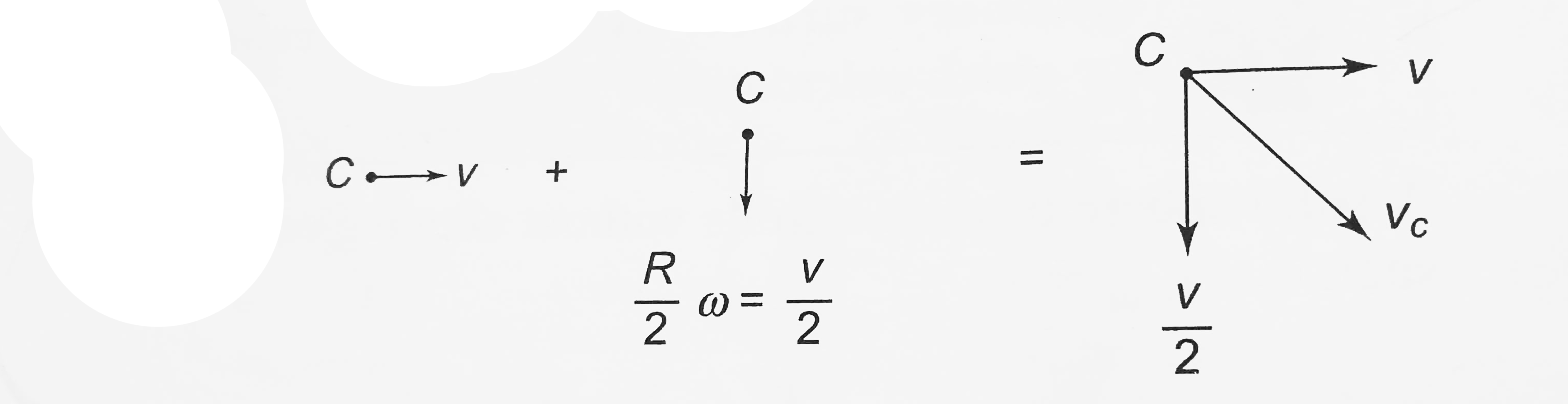 
vC=√v2+(v2)2=√5v2
Point D :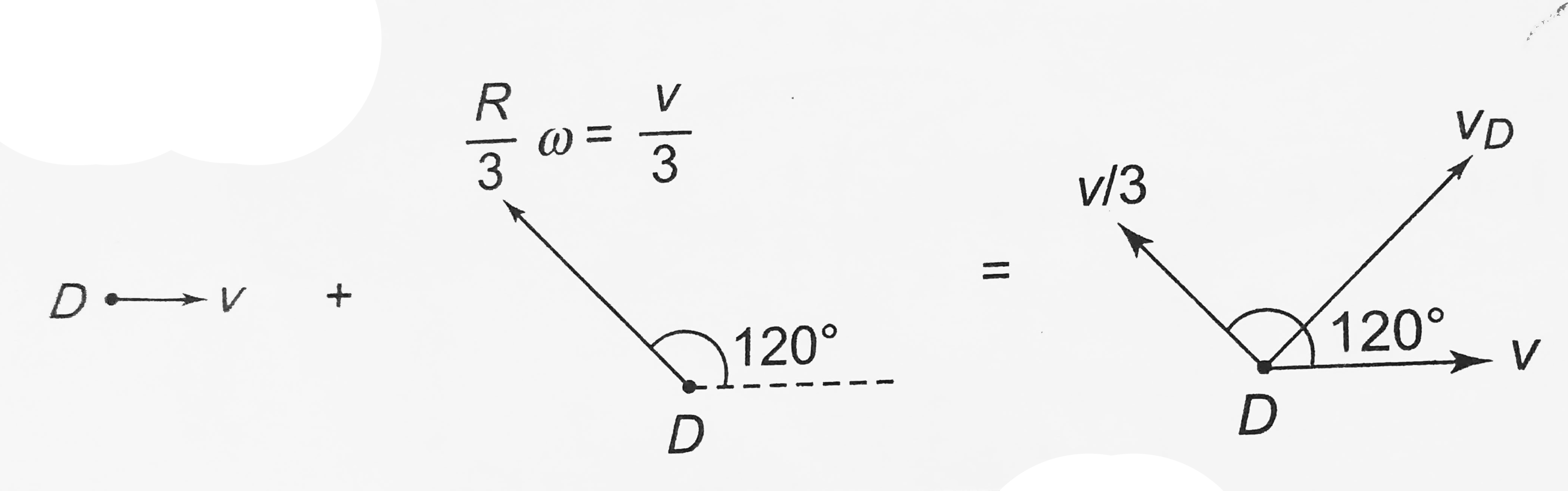 
vD=√v2+(v3)2+2×v×v3cos120∘
=√v2+(v29)−v23=√7v3
Topper's Solved these Questions
Similar Questions
A solid sphere of mass m and radius R rolls without slipping on the horizontal surface such that its velocity of center of mass is v0. Find its translational kinetic energy, rotational kinetic energy, total kinetic energy, gravitational potential energy taking surface as reference level and mechanical energy.
View SolutionA bobbin rolls without slipping over a horizontal surface so that the velocity v of the end of the thread (point A) is directed along the horizontal . A board hinged at point B leans against the bobbin (Fig.) The inner and outer radii of the bobbin are r and R respectively. Determine the angular velocity ω of teh board as a function of an angle α.
View Solution
Knowledge Check
A wheel rolls without slipping on a horizontal surface such that its velocity of center of mass is v. The velocity of a particle at the highest point of the rim is
AzeroBvC2vD√2vA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is
Av0Bv02Cv02√7Dv02√3A disc of radius R is rolling without sliding on a horizontal surface with a velocity of center of mass v and angular velocity ω in a uniform magnetic field B which is perpendicular to the plane of the disc as shown in Fig. 3.179. O is the center of the disc and P,Q,R,andS are the four points on the disc. Which of the following statements is true?
A(a) Due to translation, induced emf across PS=BvrB(b) Due to translation, induced emf across QS=0C( c) Due to translation, induced emf across RO=0D(d) Due to translation, induced emf across OQ=Bvr
A ball of radius R and mass m is rolling without slipping on a horizontal surface with velocity of its centre of mass vCM. It then rolls wilthout slippig up a hill to a height h before momentarily coming to rest. Find h
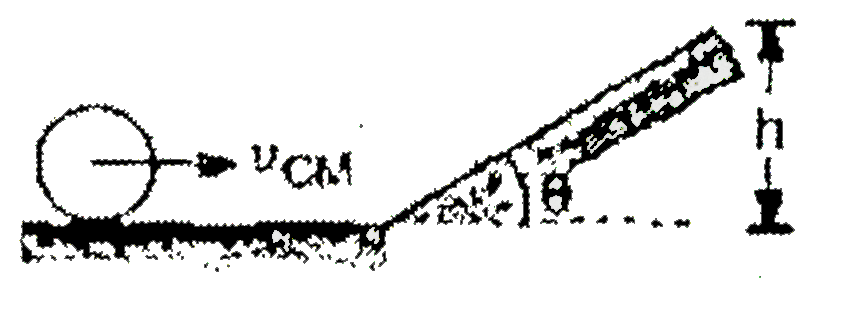
View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.
View SolutionAssertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v.
Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.
View SolutionA solid disc rolls clockwise without slipping over a horizontal path with a constant speed v. Then the magnitude of the velocities of points A,B and C (see figure) with respect to a standing observer are, respectively,
.
View SolutionA disc of radius 20CM is rolling with slipping on a flat horizontal surface. At a certain instant the velocity of its centre is 4m/s and its angular velocity is 10rad/s. The lowest contact point is O.
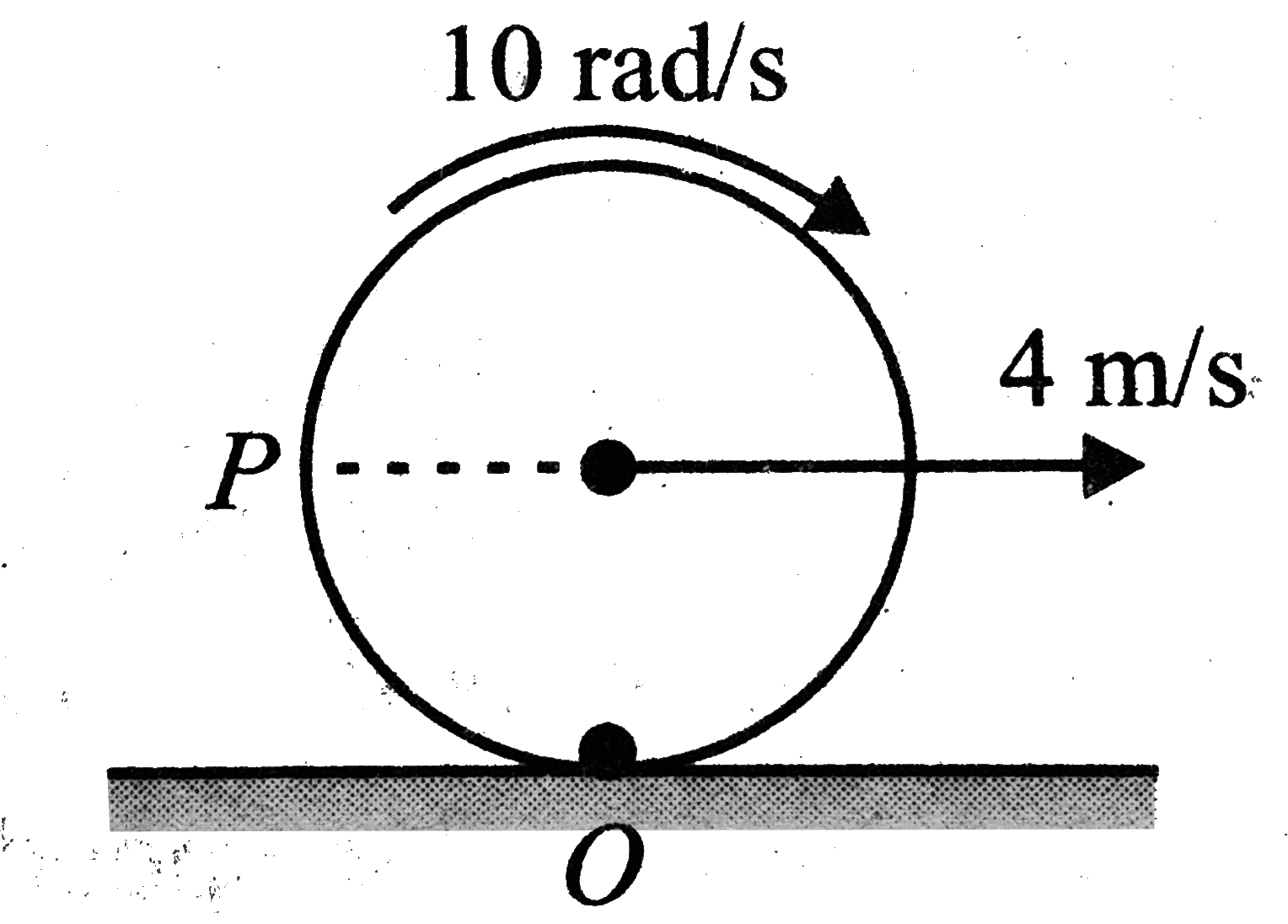
Velocity of point O is
View Solution