A material is embedded between two glass plates. Refractive index n of the material varies with thickness as shown below. The maximum incident angle (in degrees) on the material for which beam will pass through the material is-
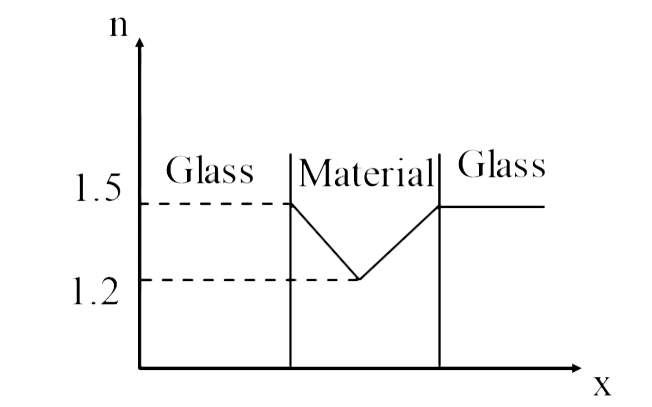
60.1
53.1
43..5
32.3
Step by step video & image solution for A material is embedded between two glass plates. Refractive index n of the material varies with thickness as shown below. The maximum incident angle (in degrees) on the material for which beam will pass through the material is- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Transparent materials like glass allow light to pass through them.
View SolutionA glass slab is made such that the refractive index of the material increases with its depth. The glass slab is kept in air and a light ray is incident on its top face. How will the light ray pass through it ?
View Solution
Knowledge Check
The refractive index of material varies with wavelength according to the Cauchy’s relation is
Aμ=Aλ+BBμ=A+Bλ2Cμ=A×BλDμ=A2λ+BRefractive index of material is equal to tangent of polarising angle. It is called
ABrewster’s lawBLambert’s lawCMalus’s lawDBragg’s lawIf critical angle for a material to air is 30∘, the refractive index of the material will be
A1.0B1.5C2.0D2.5
What is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
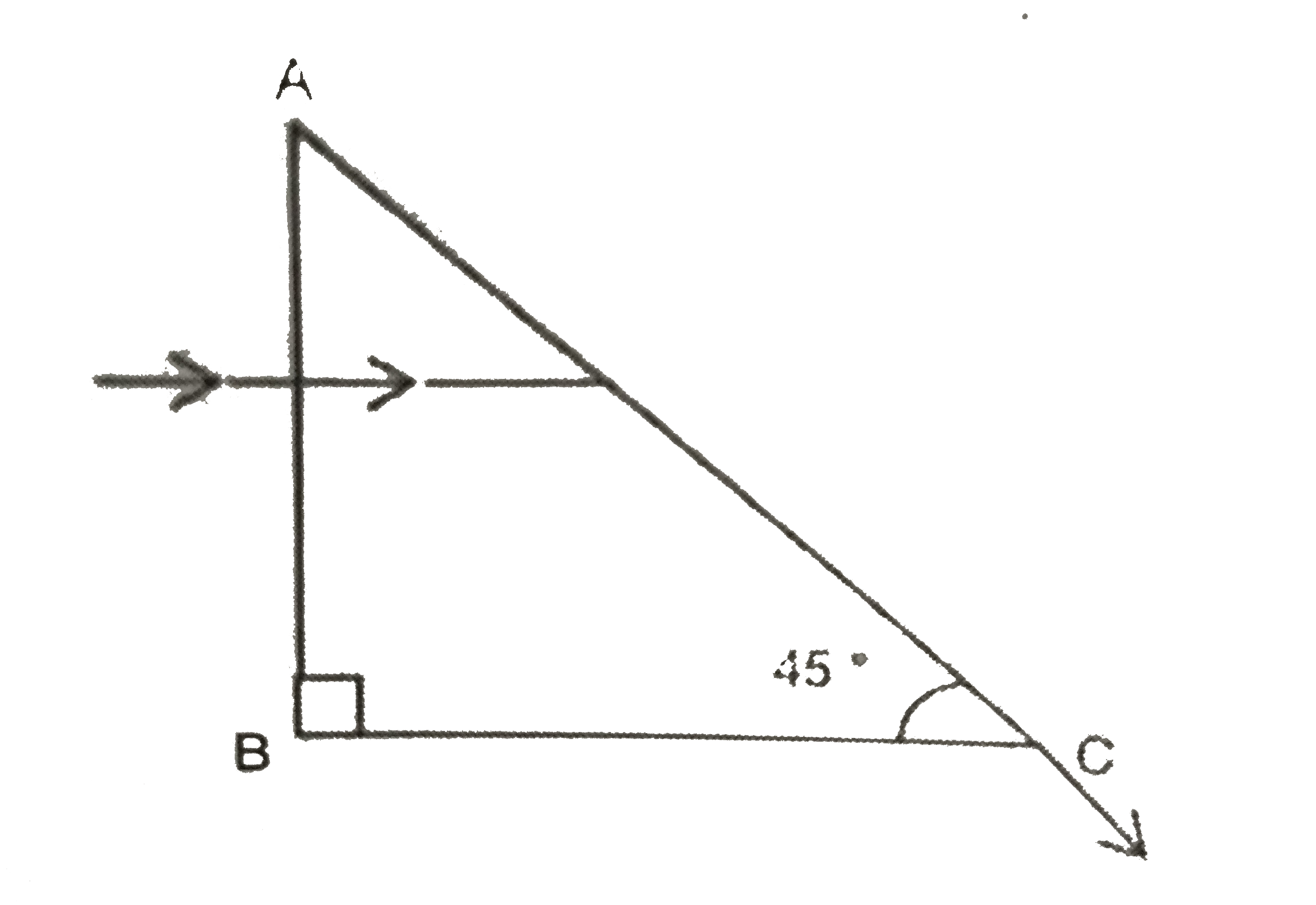
View SolutionThe refracting angle of the prism is 60∘ and the refractive index of the material of the prism is √3. Calculate the angle of minimum deviation in degree.
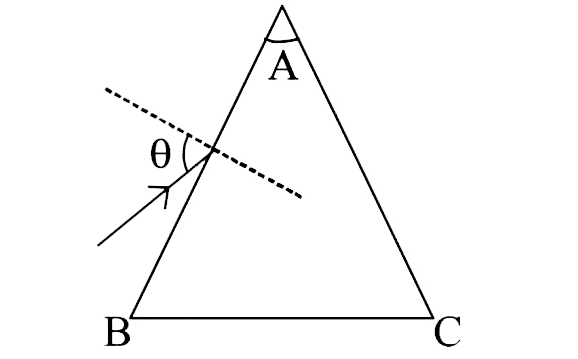
View SolutionMonochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
View SolutionThe refractive index of the material of a prism and liquid are 3/2 and 4/3 respectively. Critical angle C in glass can be expressed as
View SolutionThe refractive index of the material of a prism and liquid are 3/2 and 4/3 respectively. Critical angle C in glass can be expressed as
View Solution

