A firecracker is thrown with velocity of 30ms−1 in a direction which makes an angle of 75∘with the vertical axis. At some point on its trajectory, the firecracker splits into two identical pieces in such a way that one piece fall 27 m far from the shooting point. Assuming that all trajectories are contained in the same plane, how far will the other piece fall from the shooting point ? (Take g=10ms−2 and neglect air resistance)–
63 m or 144 m
72 m or 9 m
28 m or 72 m
63 m or 117 m
The correct Answer is:D
Step by step video, text & image solution for A firecracker is thrown with velocity of 30 ms^(-1) in a direction which makes an angle of 75^(@)with the vertical axis. At some point on its trajectory, the firecracker splits into two identical pieces in such a way that one piece fall 27 m far from the shooting point. Assuming that all trajectories are contained in the same plane, how far will the other piece fall from the shooting point ? (Take g = 10 ms^(-2) and neglect air resistance)– by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A projectile is thrown from a point O on the ground at an angle 450 from the vertical and with a speed 5√2ms. The projectile at highest point of its tracjectory splits into two equal parts. One part falls vertically down to the ground 0.5s after the splitting. The other part t seconds after the splitting falls to the ground at a distance x meters from the point O. The acceleration due to gravity g=10ms2. The value of t is
View SolutionA piece of wire is of length 1234m. if it is cut into two pieces in such a way that the length of one piece is 514m, what is the length of the other piece?
View Solution
Knowledge Check
When a projectile is at the highest point of its trajectory, the directions of its velocity and acceleration are
AParallel to each otherBanti-parallel to each otherCinclined to each other at an angle of 45 degreeDperpendicular to each otherAt the topmost point of a trajectory, its velocity and acceleration are an angle of
A0∘B45∘C90∘D180∘Three projectile A, B and C ar thrown from the same point in the same plane. Their trajectories are shown in the figure, Then which of the following statement is true -
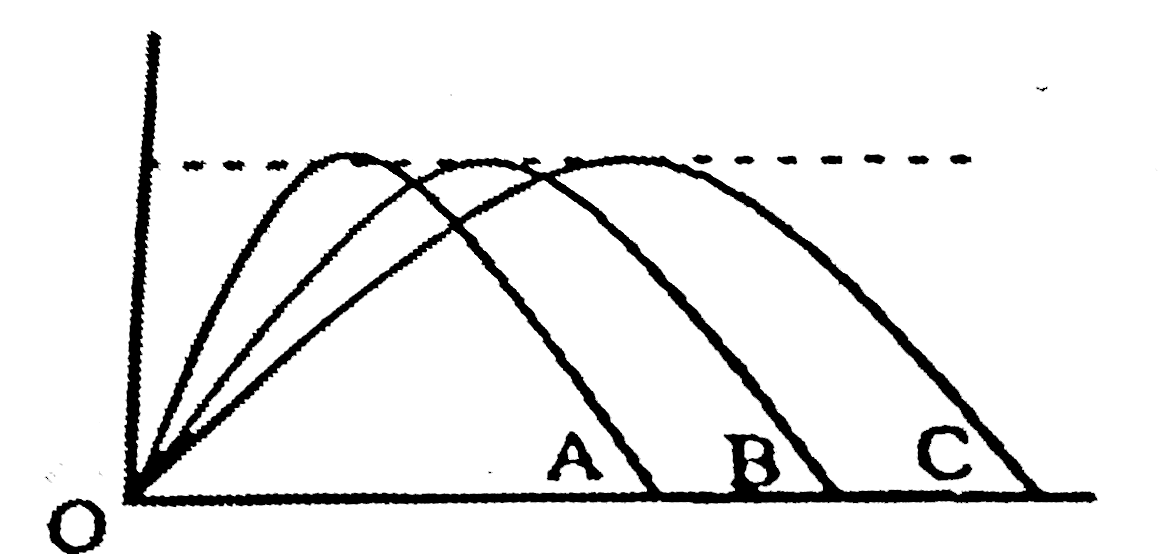 Athe time of flight is the same for all the threeBthe launch speed is greatest for particle CCthe horizontal velocity component is greatest for particle CDall of the above
Athe time of flight is the same for all the threeBthe launch speed is greatest for particle CCthe horizontal velocity component is greatest for particle CDall of the above
Four circular cardboard pieces each of radius 7 cm are placed in such a way that each piece touches two other pieces. Find the area of the space enclosed by the four pieces.
View SolutionA shell of mass 2m fired with a speed u at an angle θ to the horizontal explodes at the highest point of its trajectory into two fragments of mass m each. If one fragment falls vertically, the distance at which the other fragment falls from the gun is given by :
View SolutionA projectile of mass 20 kg is fired with a velocity of 400m/sat an angle of 45∘ with the horizontal .At the highest point of the trajectocy the projectile explodes into two fragments of equal mass,one of which falls vertically downward with zero initial speed, The distance of the point where the other fragment falls from the point offiring is:
View SolutionA 63 cm long wire is to be cut into two pieces such that one piece will be 25 as long as the other. How many centimetres will the shorter piece be?
View SolutionA particle is projected with velocity 'u' makes an angle θ w.r.t. horizontal. Now it breaks in two identical parts at highest point of trajectory. If one part is retrace its path, then velocity of other part is -
View Solution
