A block of mass m is sliding down an inclined plane with constant speed. At a certain instant t0, its height above the ground is h. The coefficient of kinetic friction between the block and the plane is $μ$ . If the block reaches the ground at a later instant $t_{g}$ , then the energy dissipated by friction in the time interval $(t_{g} - t_{0})$ is -

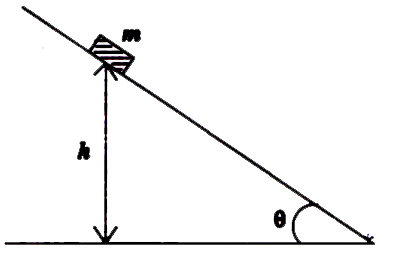
$μ m g h$

$μ m g h / sin θ$

mgh

$μ m g h / cos θ$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A block of mass m is sliding down an inclined plane with constant speed. At a certain instant t0, its height above the ground is h. The coefficient of kinetic friction between the block and the plane is mu. If the block reaches the ground at a later instant t_g, then the energy dissipated by friction in the time interval (t_(g)-t_(0)) is - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART I (Chemistry)
2 Videos

Knowledge Check

A block of mass $m$ sliding down an inclined at constant speed is initial at a height $h$ shown the ground as shown in the figure above . The coefficient of kinetic friction between the mass and the inclined is $μ$ . If the mass constinues to slide down the inclined at a constant speed how much energy is displaced by friction by the time the mass reaches the bottom of the incline?

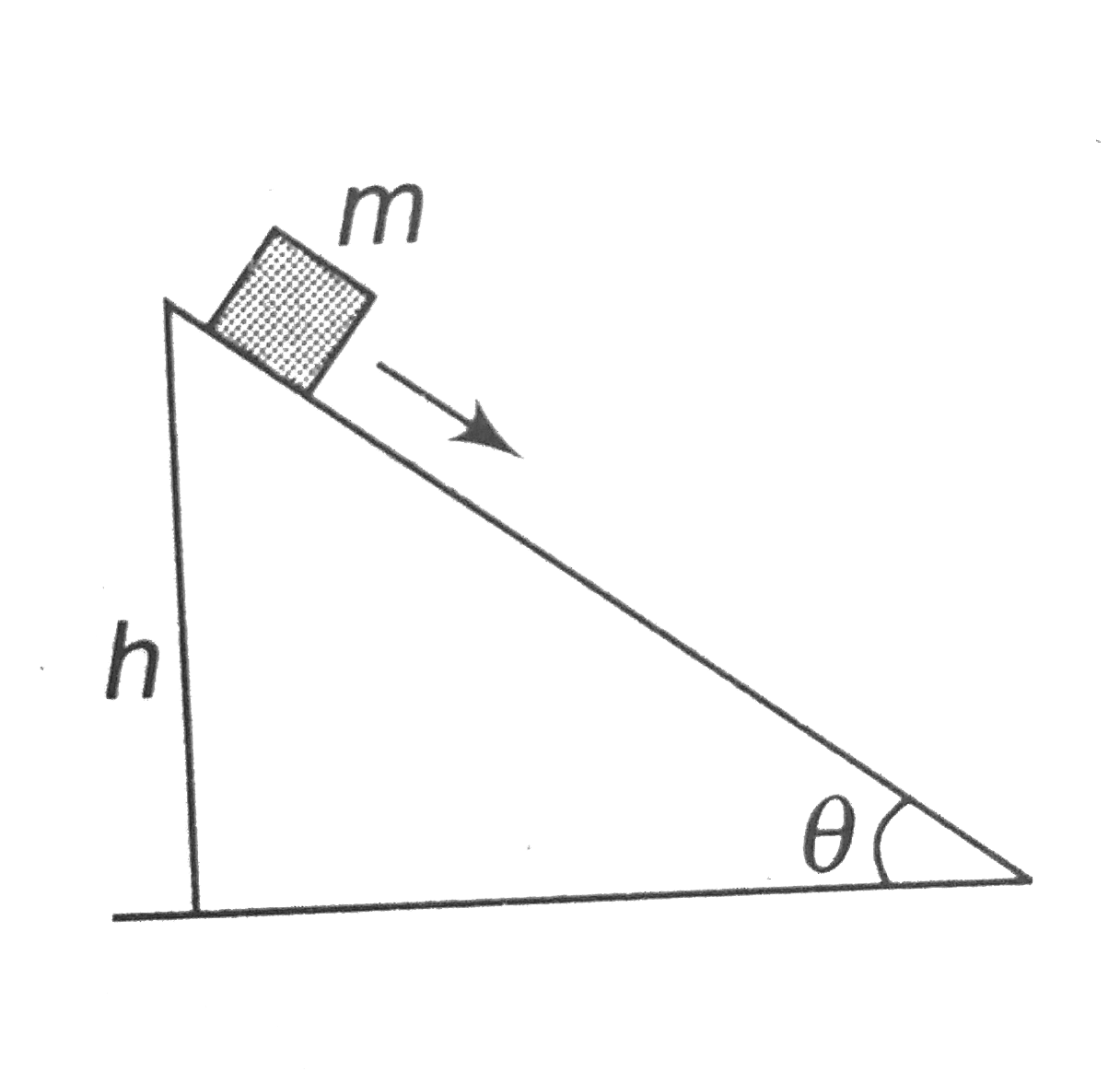A $m g h / θ$
B $m g h$
C $μ m g h / sin θ$
D $m g h sin θ$
A block of mass m slides down an inclined plane which makes an angle $θ$ with the horizontal. The coefficient of friction between the block and the plane is $μ$ . The force exerted by the block on the plane is
A $m g cos θ$
B $\sqrt{μ^{2} + 1} m g cos θ$
C $\frac{μ m g cos θ}{\sqrt{μ^{2} + 1}}$
D $μ m g θ$
A block of mass m slides down an inclined plane of inclination $θ$ with uniform speed. The coefficient of friction between the block and the plane is $μ$ . The contact force between the block and the plane is
Amg
B $m g sin θ \sqrt{1 + μ^{2}}$
C $m g sin θ$
D $\sqrt{{(m g sin θ)}^{2} + {(μ m g cos θ)}^{2}}$

KVPY PREVIOUS YEAR-KVPY-All Questions

Home
Ask Doubt
Profile

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is

A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is

KVPY PREVIOUS YEAR-KVPY-All Questions

A block of mass m slides down an inclined plane which makes an angle $θ$ with the horizontal. The coefficient of friction between the block and the plane is $μ$ . The force exerted by the block on the plane is

A block of mass m slides down an inclined plane of inclination $θ$ with uniform speed. The coefficient of friction between the block and the plane is $μ$ . The contact force between the block and the plane is