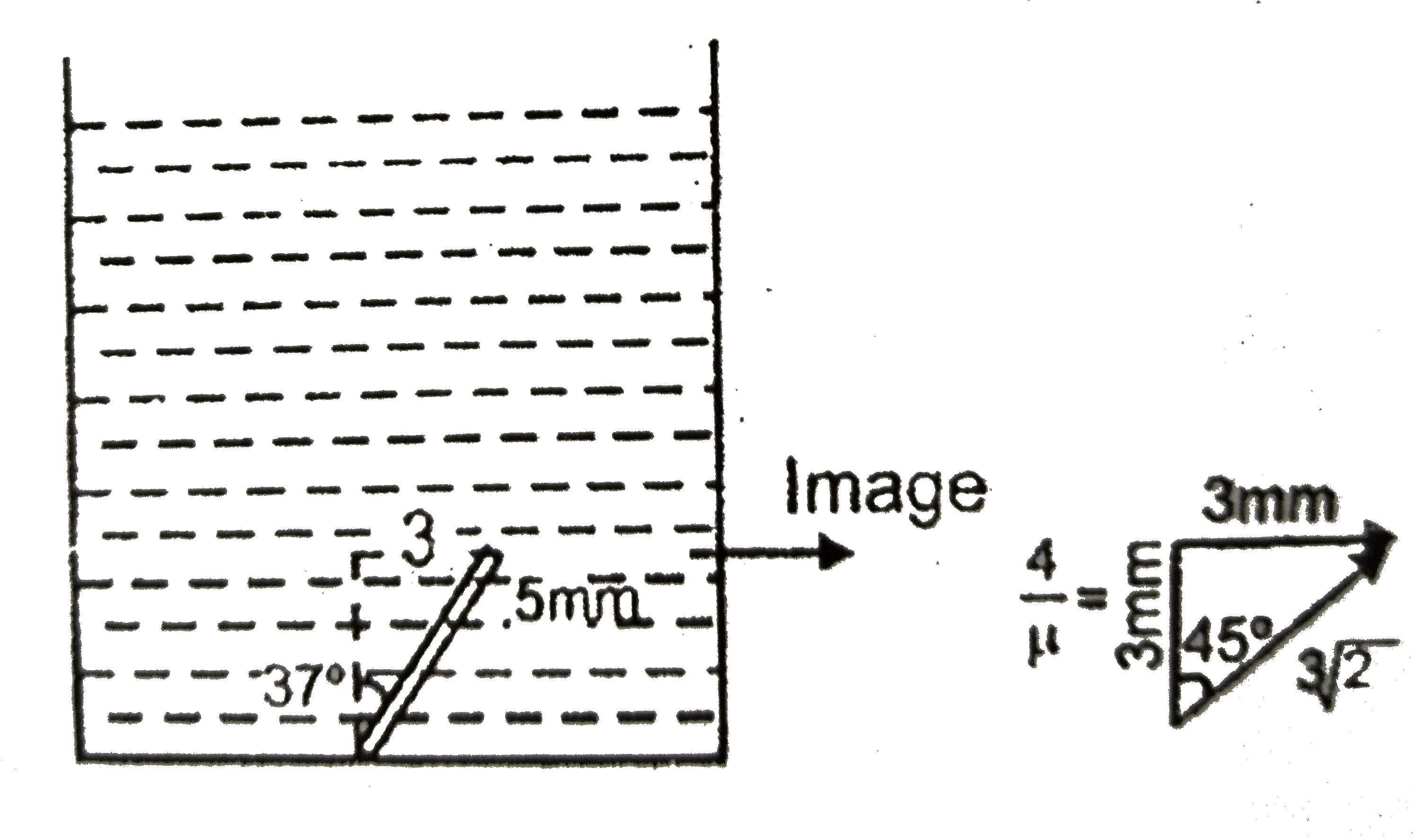A small wooden rod of length 5mm is fixed at the bottom of the container filled with water (μwater=43). It is making an angle 37∘ with vertical. If an observer (in air) observes the rod paraxially, and the rod is appearing at an angle πx radian with vertical then the find the value of x. 
The correct Answer is:4
Similar Questions
A rod of length 1m and mass 0.5kg is fixed at one end is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required ?
View SolutionA rod of length 1.0m and mass 0.5kg fixed at ond is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required?
View Solution
Knowledge Check
A wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
A20cmB40cmC60cmD75cmA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 Amg/2B2mgCmg/2√3D√3mg
Amg/2B2mgCmg/2√3D√3mg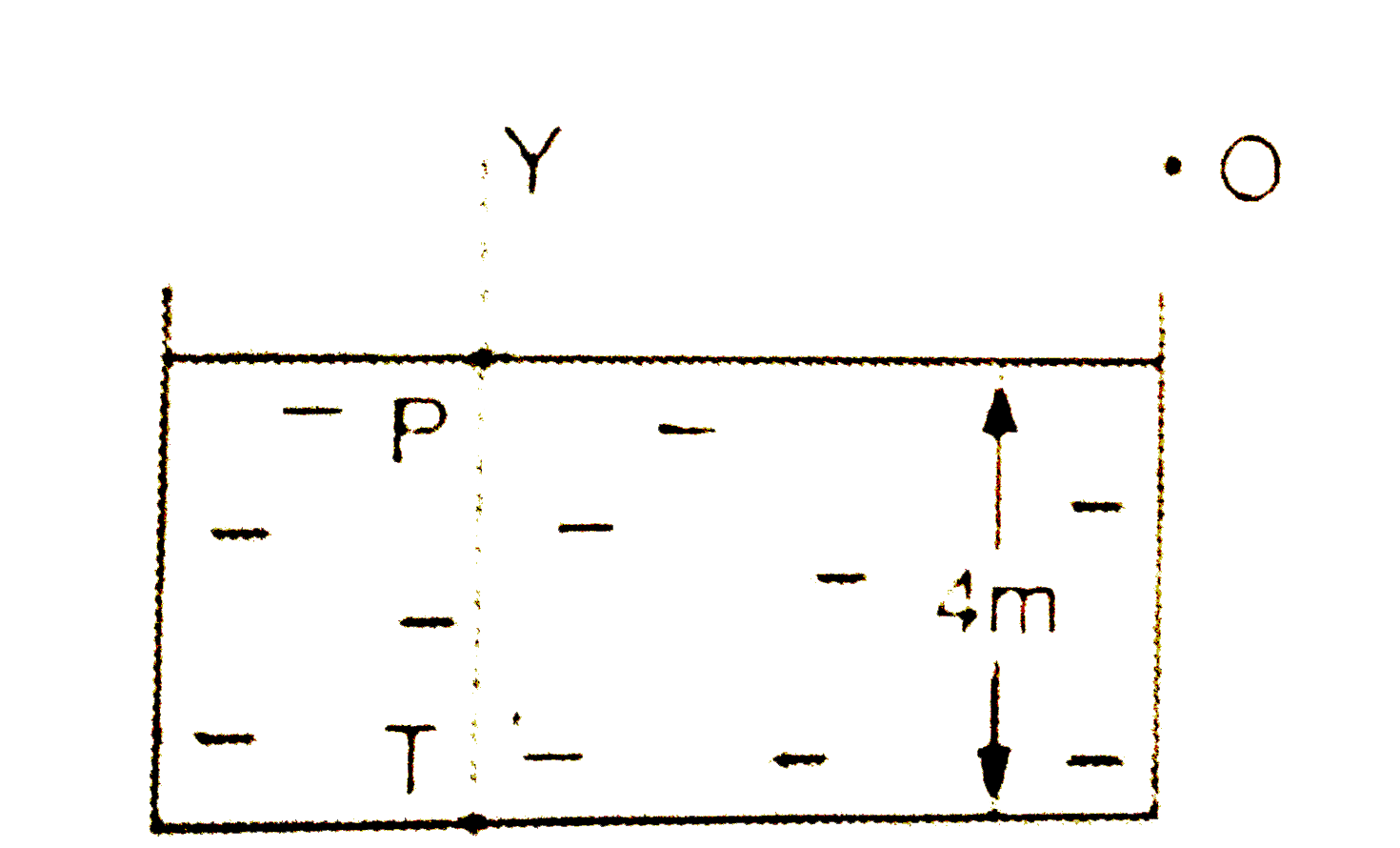
T is a point at the bottom of a tank filled with water, as shwon. The refractive index of water is 4/3. YPT is the vertical line through T. To an observer at the position O,T will appear to beAto the left of YTBsomewhere on YTCat a depth 3m below TDat a depth <3m below T
A small piece of wood is floating in the water of depth 1m . The refractive index of water is 4/3 and the sum rays are incident at an angle of 53∘ to the vertical. Find the location of the shadow of the wood piece on the bottom of the ocean.
View SolutionA small rod ABC is put in water making an angle 6∘ with vertical. If it is viewed paraxially from above, it will look like bent shaped ABC'. The angle of bending (∠CBC') will be in degree is (nw=43).

View SolutionA rectangular tank contains water to a height h. A metal rod is hinged to the bottom of the tank so that it can rotate freely in the vertical plane. The length of the rod is L and it remains at rest with a part of it lying above the water surface. In this position the rod makes an angle θ with the vertical. Assume thaty=cosθ and find fractional change in value of y when temperature of the system increases by a small value ΔT.Coefficient of linear expansion of material of rod and the tank areα1 and α2 respectively. Coefficient of volume expansion of water is λ. What is necessary condition for θ to increase?
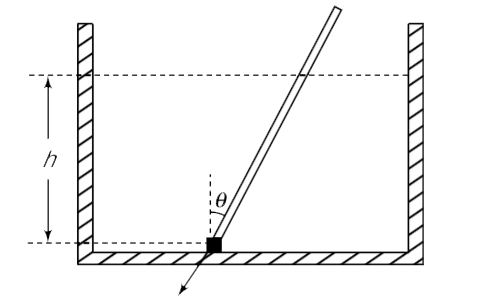
View SolutionA ship is salling in river. An observe is situated at a depth h in water (μw). If x>>h, find the angle made form vertical, of the line of slight of ship.

View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.
View Solution