A rod of length 1m and mass 0.5kg is fixed at one end is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required ?
The correct Answer is:[1.225J]
To solve the problem of how much work is required to raise the rod from a vertical position to an angle of 60 degrees with the vertical, we can follow these steps:
Step 1: Identify the mass and length of the rod
- The mass of the rod, m=0.5kg
- The length of the rod, L=1m
Step 2: Determine the initial position of the center of mass
- When the rod is hanging vertically, the center of mass is located at the midpoint of the rod.
- Therefore, the initial height of the center of mass from the reference level (ground) is:
hi=L2=12m=0.5m
Step 3: Determine the final position of the center of mass
- When the rod is raised to an angle of 60∘ with the vertical, we need to find the new height of the center of mass.
- The center of mass will be at a distance of L2 from the fixed end, which can be calculated using trigonometry:
hf=L2cos(60∘)=12⋅12=14m=0.25m
Step 4: Calculate the change in height of the center of mass
- The change in height h of the center of mass when the rod is raised is:
h=hi−hf=0.5m−0.25m=0.25m
Step 5: Calculate the work done
- The work done W in raising the center of mass can be calculated using the formula:
W=mgh
where g is the acceleration due to gravity (approximately 9.81m/s2).
- Substituting the values:
W=0.5kg⋅9.81m/s2⋅0.25m
W=0.5⋅9.81⋅0.25=1.22625J
Final Answer
The work done in raising the rod to an angle of 60∘ with the vertical is approximately 1.23J.
---
- The mass of the rod, m=0.5kg
- The length of the rod, L=1m
- When the rod is hanging vertically, the center of mass is located at the midpoint of the rod.
- Therefore, the initial height of the center of mass from the reference level (ground) is:
hi=L2=12m=0.5m
- When the rod is raised to an angle of 60∘ with the vertical, we need to find the new height of the center of mass.
- The center of mass will be at a distance of L2 from the fixed end, which can be calculated using trigonometry:
hf=L2cos(60∘)=12⋅12=14m=0.25m
- The change in height h of the center of mass when the rod is raised is:
h=hi−hf=0.5m−0.25m=0.25m
- The work done W in raising the center of mass can be calculated using the formula:
W=mgh
where g is the acceleration due to gravity (approximately 9.81m/s2).
- Substituting the values:
W=0.5kg⋅9.81m/s2⋅0.25m
W=0.5⋅9.81⋅0.25=1.22625J
The work done in raising the rod to an angle of 60∘ with the vertical is approximately 1.23J.
Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:Advance McQ
Explore 20 Videos
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Unsolved Numerical Pro.
Explore 83 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
Similar Questions
A rod of length 1.0m and mass 0.5kg fixed at ond is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required?
View SolutionA uniform rod of length L and mass M is pivoted freely at one end and placed in vertical position.
a. What is angular acceleration of the rod when it is at an angle θ with the vertical?
b. What is the tangential linear acceleration of the free end when the rod is horizontal?
View Solution
Knowledge Check
A body of mass m hangs at one end of a string of length l , the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at mean position is
A2mgBmgC3mgD√3mgA body of mass m hangs at one end of a string of lenth l, the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at bottommost point position is
A2 mgBmgC3 mgD√3mgA body of mass m hangs at one end of a string of length l, the other and of which is fixed . It is given a horizontal velocity so that the string would just reach where it makes an angle of 30∘ with the vertical . The tension in the string at mean position is
Amg(5−2√3)Bmg(3−3√3)Cmg(3−√3)Dmg(4−√3)
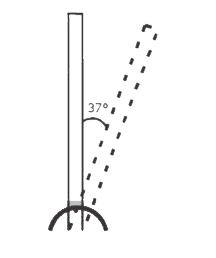
A uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
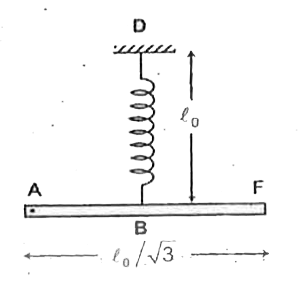
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View SolutionA bob of mass 2 kg hangs from a string of length 5 m . It swings from its rest position to one of the sides so that the string makes an angle of 60∘ with the vertical Calculate the gain in potential energy of the bob .
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle 45∘ with the initial vertical direction is
View Solution

