Two identical small balls are suspended by ends of a rod. Whole assembly is rotating about vertical axis passing through center of rod. At a certain value of ω both strings make 37° with vertical. Find ω
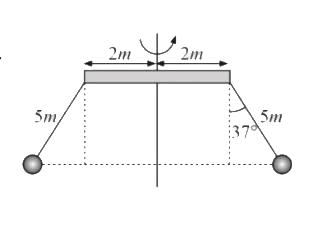
√23 rad/sec
√73 rad/sec
√32 rad/sec
√52 rad/sec
The correct Answer is:C
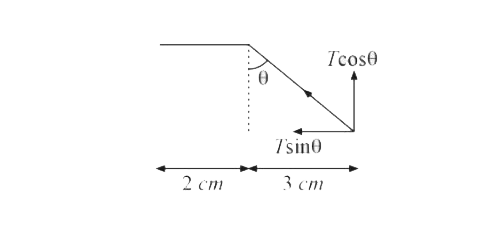
Tcosθ=mg
Tsinθ=mω2r
tanθ=ω25g
ω=√32 rad/sec
Similar Questions

A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
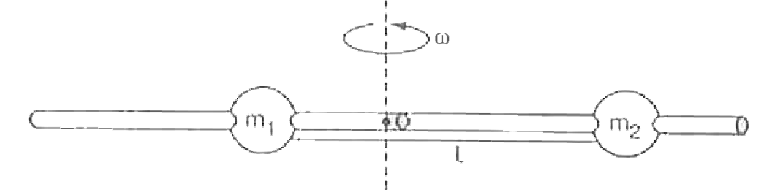
View SolutionTwo balls of masses m1=0.5kgandm2=0.3kg are connected by a nonstretchable string and slipped on to a horizontal , light rod. The rod is rotated with ω=110 rpm about a vertical axis passing through its centre. Find the tension of the string and the distance of the masses from the axis of rotation if l=20 cm is the length of the string. Is the equilibrium of the balls stable ?
View Solution
Knowledge Check
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotationif rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
ABωL24BBωL22C3BωL24DzeroA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
Amω2l23AYBmω3l33AYCmω2l34AYDmω3l23AY
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionThree identical thin rods, each of length L and mass m, are welded perpendicular to one another as shown in figure. The assembly is rotated about an axis that passes through the end of one rod and is parallel to another. The moment of inertia of this structure about this axis is.
 .
.
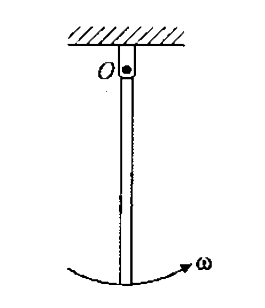
View SolutionA thin uniform heavy rod of length l hangs from a horizontal axis passing through one end. The initial angular velocity ω that must be imparted to it to rotate it through 90∘ is :
View Solution
