The motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
4a
12a
6a
8a
The correct Answer is:D
To solve the problem, we need to find the distance traveled by a particle in the first 4 seconds given the equation of motion u=at.
1. Understand the Equation: The equation given is u=at. Here, u represents the velocity of the particle at time t, and a is the constant acceleration.
2. Identify Initial Conditions: At t=0, the initial velocity u0=0 (since u=at implies u0=a⋅0=0).
3. Use the Equation for Distance: The formula for the distance s traveled under constant acceleration is:
s=ut+12at2
where u is the initial velocity, a is the acceleration, and t is the time.
4. Substitute Known Values: We know:
- Initial velocity u=0
- Time t=4 seconds
- Acceleration a (remains as a variable since it is not specified)
Plugging these values into the distance formula:
s=0⋅4+12a(42)
Simplifying this gives:
s=12a⋅16=8a
5. Conclusion: The distance traveled by the particle in the first 4 seconds is:
s=8a
Final Answer:
The distance traveled by the particle in the first 4 seconds is 8a.
---
s=ut+12at2
where u is the initial velocity, a is the acceleration, and t is the time.
- Initial velocity u=0
- Time t=4 seconds
- Acceleration a (remains as a variable since it is not specified)
s=0⋅4+12a(42)
Simplifying this gives:
s=12a⋅16=8a
s=8a
The distance traveled by the particle in the first 4 seconds is 8a.
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Relative Motion
13 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Motion Under Gravity
81 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN ONE DIMENSIONEXERCISE - Uniform Motion
24 Videos
- GRAVITATIONBOOK - ERRORLESS CHAPTER - GRAVITATIONEXERCISE - SET
27 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise
319 Videos
Similar Questions
The potential energy (in SI units) of a particle of mass 2kg in a conservative field is U=6x−8y. If the initial velocity of the particle is →u=−1.5ˆi+2ˆj, then find the total distance travelled by the particle in the first two seconds.
View SolutionConsider the previous problem
(a) When does the particle reach A again?
(b) Locate the point where the particle reverses its direction of motion.
(c) Find the distance travelled by the particle in the first 15 seconds.
View Solution
Knowledge Check
The distance travelled by the particle is
A8 cmB2 cmC4 cmDzeroThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
A1 mB2 mC2.5 mD3 mThe position of a particle moving rectilinearly is given by x=t3−3t2−10. Find the distance travelled by the particle in the first 4 seconds starting from t=0.
A24 unitB36 unitC15 unitD50 unit
A particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
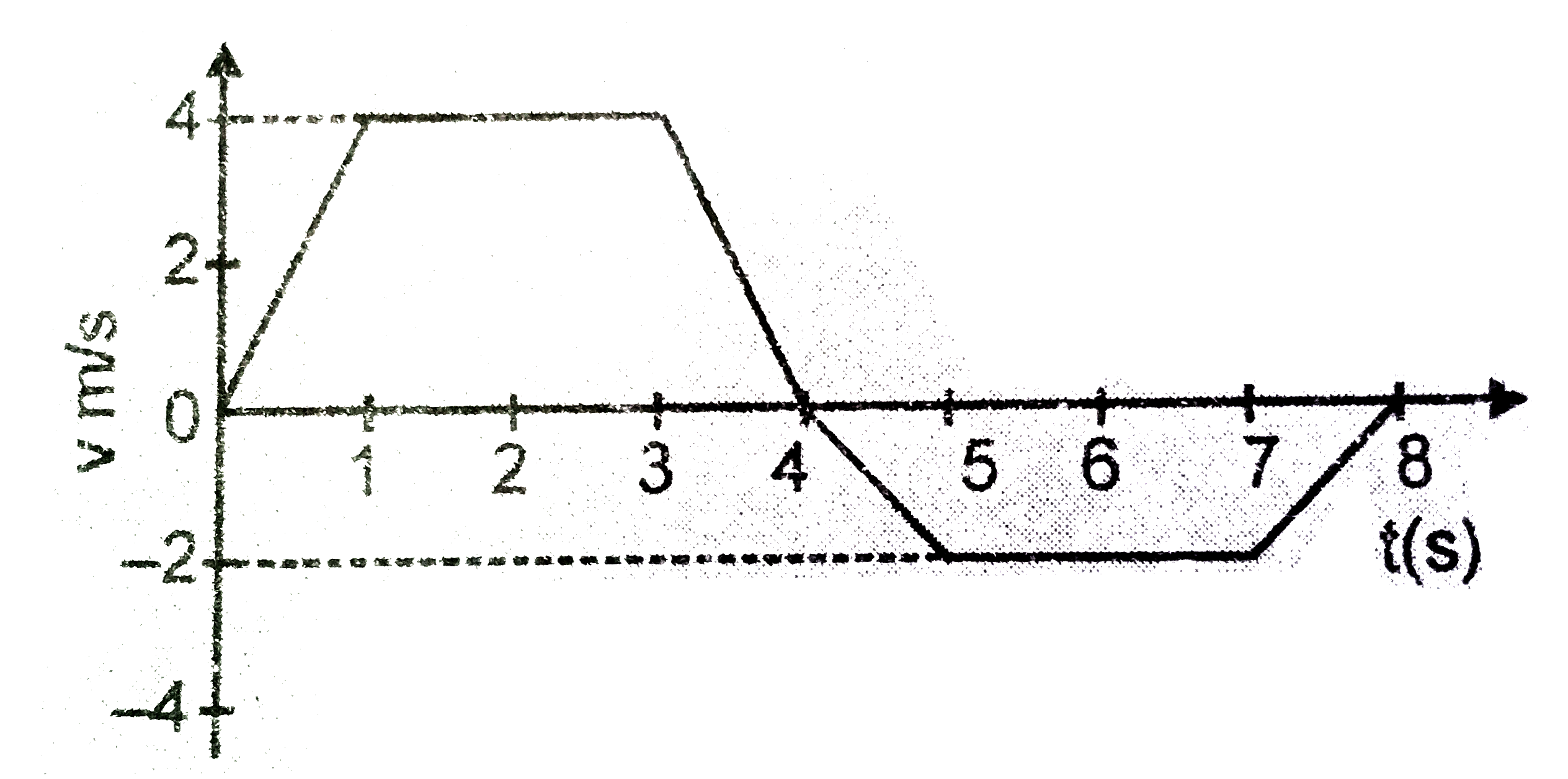
View SolutionThe velocity of a particle varies with time as per the figure shown. The distance travelled by the particle in 10 seconds is ?(m/s)
View SolutionA particle is thrown up with an initial velocity such that it takes more than one second to reach the top point. What is the distance travelled by the particle during the first second of its decent?
View SolutionVelocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
View SolutionThe variation of velocity of a particle with time moving along a straight line is illustrated in the following figure. The distance travelled by the particle in four seconds is.
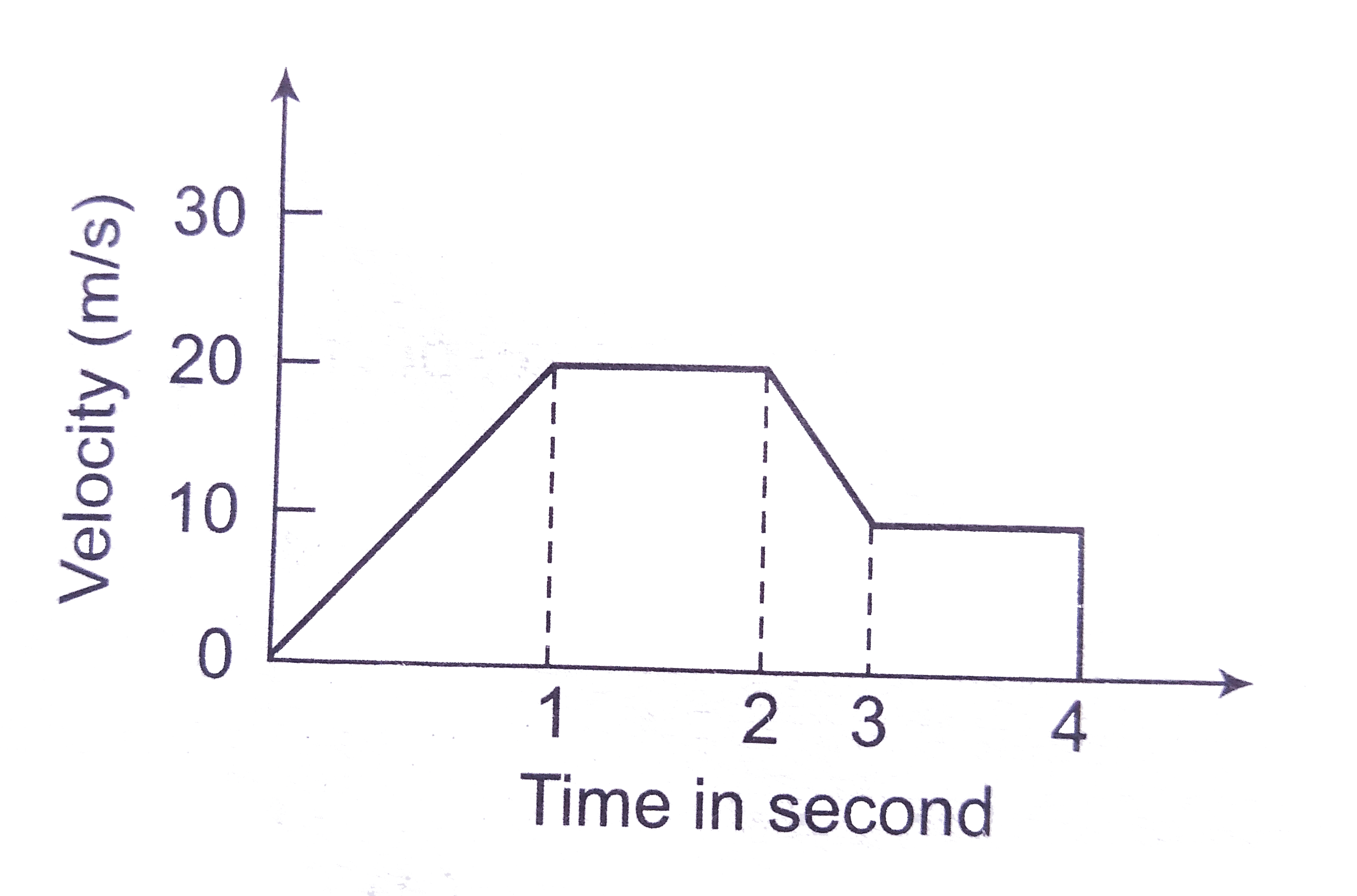
View Solution
