Consider the previous problem
(a) When does the particle reach A again?
(b) Locate the point where the particle reverses its direction of motion.
(c) Find the distance travelled by the particle in the first 15 seconds.
(a) When the particle reaches the point A again, say at time t, its displacement is zero.
⇒0=ut+12at2
⇒0=12t+12(−1)t2
⇒t=0and=24s
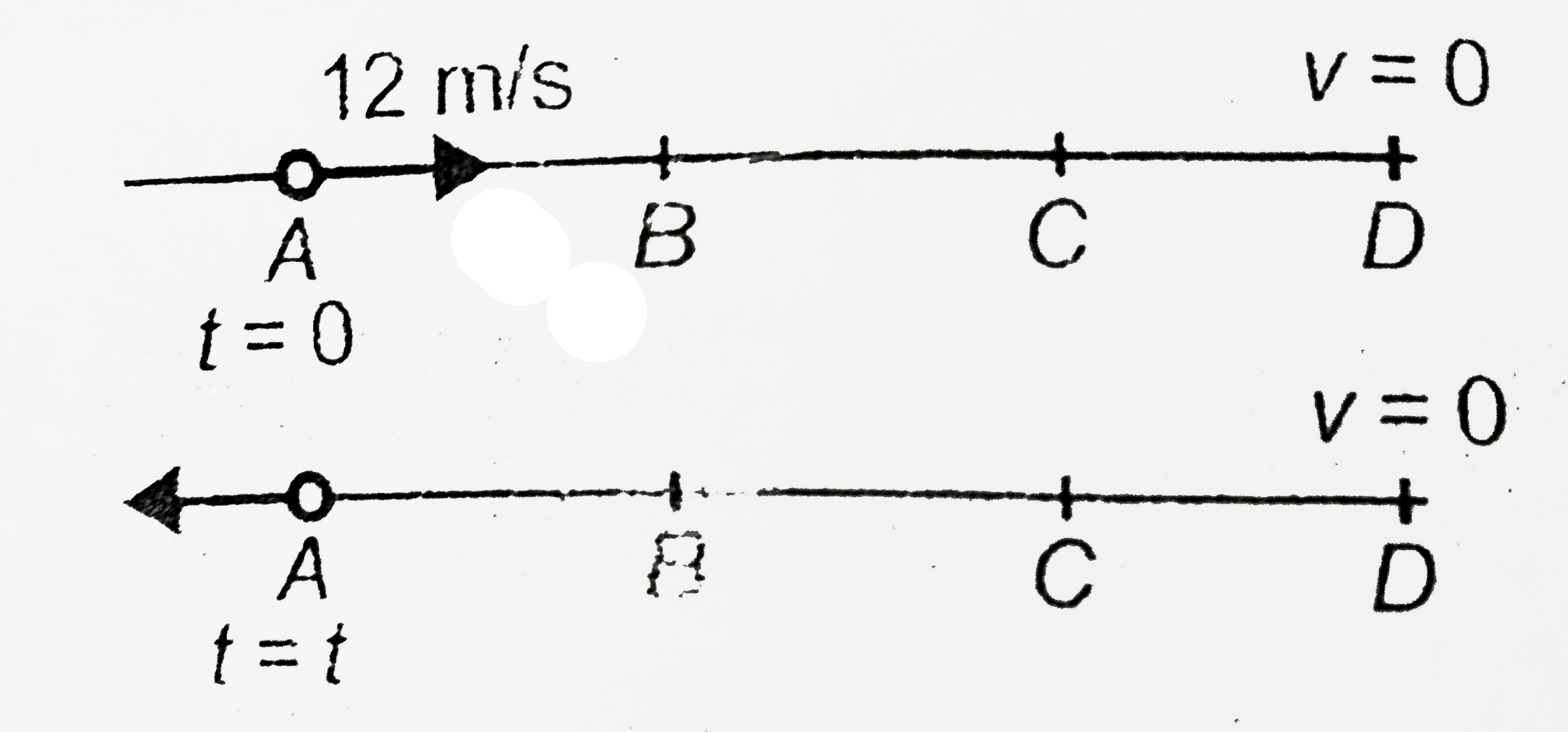
As t = 0 is the initial moment, t = 24 s is the moment when the particle reaches. A again
(b) Let the particle reverse its direction of motion at D, then the speed of particle at D will be zero. For the interval A to D
u=12m/s,a=−1m/s2,AD=s,v=0
⇒02=(12)2+2(−1)(s) [from v2=u2+2as]
Ypu can also calculate the time taken by the particle to reach D from v=u+at,0=12+(−1)tD and then from s=12dtD+12(−1)t2D, you can find s. But then again you must be interested in optimizing the steps of calulation and must not proceed in the above manner.
(c) Can you use the equation s=ut+12at2 to find the distance travelled in the interval?
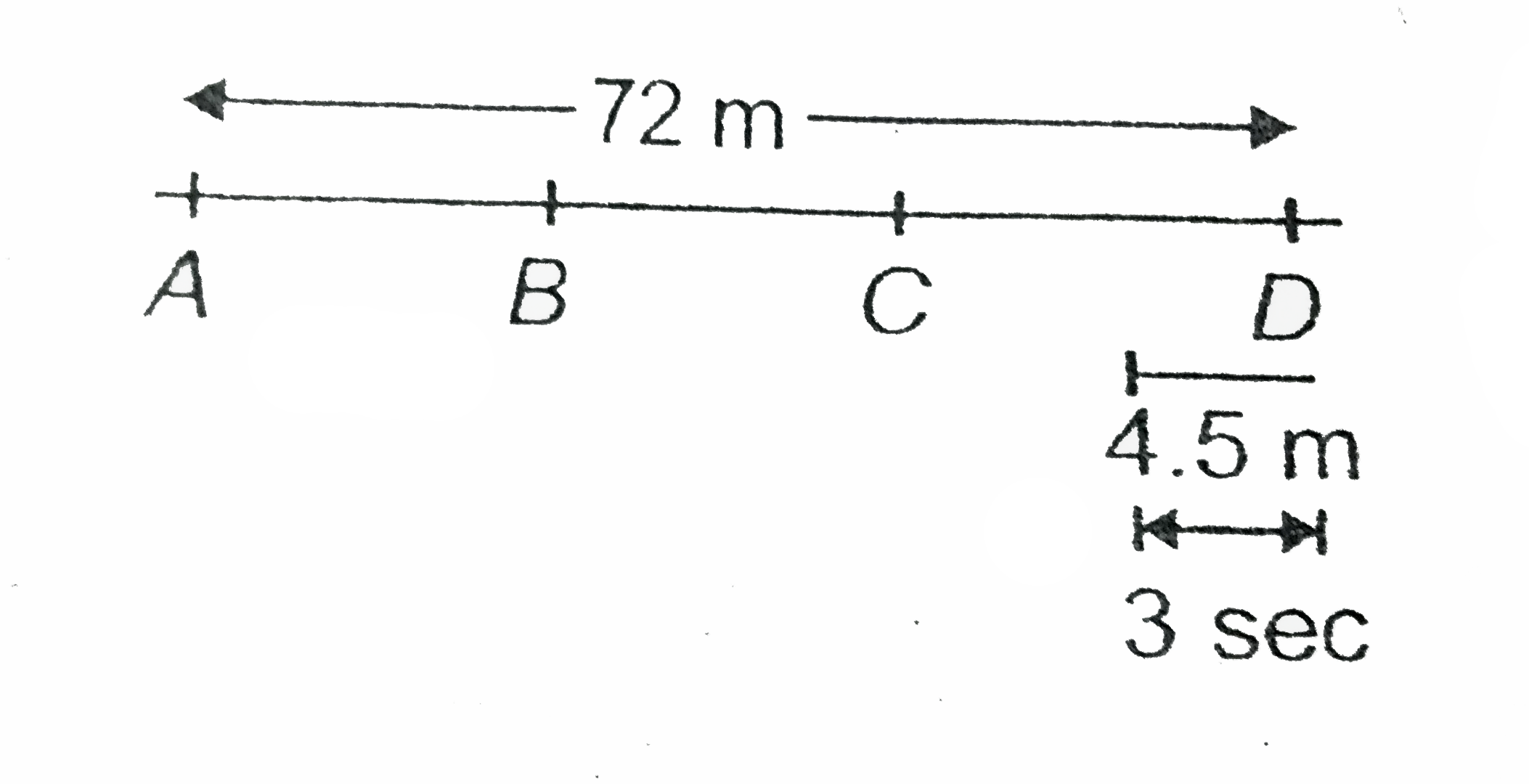
The answer will be ''Yes'' if the particle moves without reversing its direction of motion in the specified interval but the answer will be ''No'' if the particle reverses its direction of motion in the specified interval of time.
In the present problem, in the interval of 15 s the particle reverses its direction of motion at t = 12 s.
Here, first find the distance travelled in 12 s and then the distance travelled in subsequent 3 s, then add them up. We have already found AD = 72 m. Now for the subsequent 3 s interval,
u=0,a=−1m/s2,t=3s
Distance =|s|=∣∣∣0×3+12×(−1)×32∣∣∣=4.5m
⇒ Distance covered in 15 s =72+4.5=76.5m
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Try Yourself
Explore 40 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - A)
Explore 50 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTEChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
A particle moving with uniform acceleration along a straight line ABC rosses point A at t=0 with a velocity 12ms−1. is 40m away from A andC is 64m away from A. The particle passes B at t=4 s.<br>a.Afterwˆtimewillthepartic≤beatC?<br>b.WˆisitsvelocityatC?<br>c.Wˆdoesthepartic≤reachAaga∈?<br>d.Locatethep∮wherethepartic≤reversesitsdirectionofmotion.<br>e.F∈dthedistancecoveredbythepartic≤∈thefirst15 s.
View SolutionSpeed time graph of a particle shown in figure. Find distance travelled by particle in 5second.
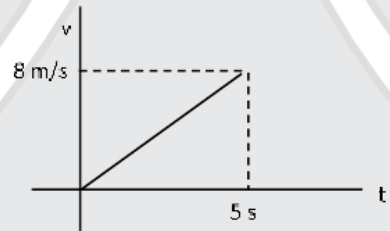
View Solution
Knowledge Check
The motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
A4aB12aC6aD8aThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
A1 mB2 mC2.5 mD3 mA particle is thrown with any velocity vertically upward, the distance travelled by the particle in first second of its decent is
AgBg2Cg4DCannot be calculated
The po9sition of aparticle is given by the equation.
s=f(t)=t3−6t2−9t
where r is is measure in seconds and s in meters.
(a). Find the velocity at the t
(b). What is thhe velocity after 2s ? After 4 s ?
(c). When is the particle at rest ?
(d). When is the particle moving formward that is, ini the positive direction)?
(e). Find the total distance traveled by the particle during the first five sec.?
View Solutionx−t equation of a particle in SHM is
x=(4cm)cos(π2t)
Here ,t is in seconds. Find the distance travelled by the particle in first three seconds.
View SolutionFrom the v versus t graph of figure (a) the time (s) at which the particle is at rest (b) at what time, if any does the particle reverse the direction of its motion? (c) The distance and displacement of the particle from t=0s to t=6 s.
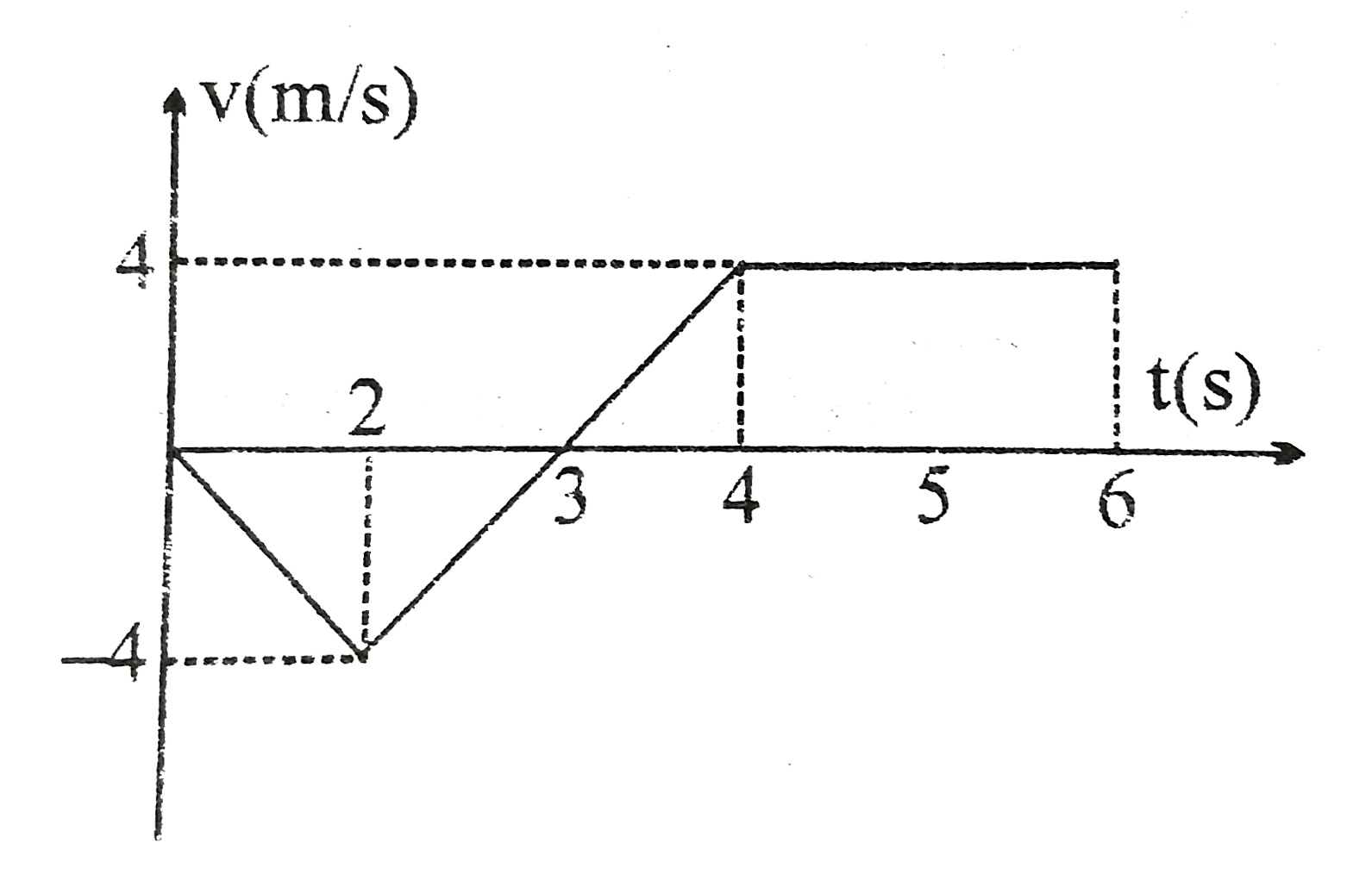
View SolutionIf S=3t3+9t2+2t+7 , then distance travelled by the particle during the first second of its motion is
View SolutionThe position of a particle moving rectilinearly is given by x=t3−3t2−10. Find the distance travelled by the particle in the first 4 seconds starting from t=0.
View Solution

